Prismas (2º ESO)
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 216)
Prismas
La siguiente actividad condensa todo lo que vamos a ver en este tema.
Actividad interactiva sobre los prismas:
- Definición.
- Elementos.
- Clasificación.
- Desarrollo plano.
- Área y volumen.
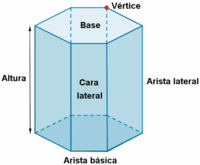
Prisma: definición y elementos. Actividad en la que se presentan distintos tipos de prismas y en la que podrás ver sus elementos. | Elementos de un prisma
de http://calculo.cc |
Clasificación de los prismas
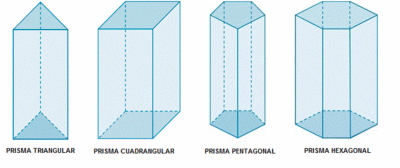
- Atendiendo a sus bases: En función del polígono de las bases, los prismas pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.
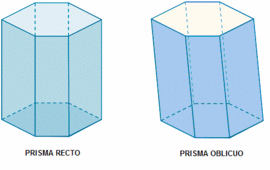
- Atendiendo a su inclinación: Si las caras laterales son perpendicualres a las bases (son rectángulos), el prisma es recto, si no , es oblicuo.
- Atendiendo a su regularidad: Un prisma es regular si su base es un polígono regular. En caso contrario es irregular. En una prisma regular, todas las aristas laterales son iguales y las caras laterales son rectángulos iguales
Clasificación de los prismas.
Dibuja un prisma de base pentagonal y recuenta sus caras, vértices y aristas.
Actividad en la que se presentan distintos tipos de prismas regulares.
Actividad interactiva en la que aprenderás los elementos y la clasificación de los prismas regulares.
Atendiendo a su inclinación
de http://calculo.cc | Atendiendo a su base
de http://calculo.cc |
Paralelepípedos
- Los paralelepípedos son prismas en los que todas sus caras son paralelogramos.
- Las bases han de ser paralelogramos y por tanto los paralelepípedos son prismas cuadrangulares.
- Entre ellos destacamos cuatro en particular:
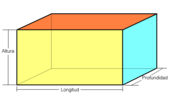
- Ortoedro: sus caras son rectángulos.
- Cubo: sus caras son cuadrados.
- Romboedro: Todas sus caras son rombos.
- Romboiedro: Todas sus caras son romboides.
Actividad en la que podrás conocer los paralelepípedos y sus distintos tipos.
Ortoedro
| Ortoedro
|
Ortoedro
| Ortoedro
|
Desarrollo plano de un prisma
Si representamos en un plano todas las caras de un prisma, de forma contigua, obtenemos lo que se denomina desarrollo plano del prisma.
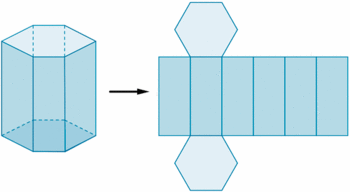
Fíjate en el siguiente prisma hexagonal. Si cortásemos adecuadamente el prisma, siguiendo ciertas aristas, podríamos desplegarlo como se muestra en la siguiente figura.
de http://calculo.cc
Actividad en la que se presentan los desarrollos planos de distintos prismas rectos regulares.
Dibuja el desarrollo plano del siguiente poliedro.
Superficie del prisma
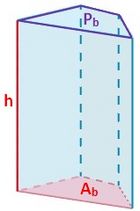
La superficie o área del prisma es igual a la suma del área de las dos bases y del área lateral.
- El área de las bases es la suma de las áreas de dos polígonos iguales.
- El área lateral es la suma de las áreas de los rectángulos que forman las caras laterales.
|
|
En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas.
- 0:00-1:40: Definición de prisma recto.
- 1:30-4:12 :Superficie lateral del prisma recto.
- 4:12-5:12 :Superficie total del prisma recto.
- 5:12-6:09 :Volumen del prisma recto.
- 6:09-12:54: Problema: Halla el área lateral, el área total y el volumen de un prisma triangular regular de 5 cm de arista básica y 7 cm de altura.
Cálculo del área total y el volumen de un prisma. Ejemplos.
Área y volumen del prisma recto.
En este vídeo de MasterD, se pretende dejar claros todos los conceptos relacionados con los prismas. Daremos una definición, explicaremos cuáles son sus partes, veremos cómo se pueden clasificar con algunos ejemplos y finalmente pasaremos a ver el área y el volumen.
Halla el área de un prisma recto regular triangular sabiendo que el lado de la base mide 3 cm y la altura 10 cm.
Halla el área de un prisma recto regular pentagonal sabiendo que el lado de la base mide 3 cm, la apotema 2.1 cm y la altura 6 cm.
Halla el área de un prisma recto regular hexagonal sabiendo que la arista básica mide 6 cm y la altura 10 cm.
Ejercicios propuestos
|
Ejercicios propuestos: Prismas |
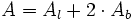
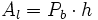
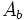 : Área de la base.
: Área de la base.
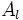 : Área lateral.
: Área lateral.
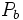 : Perímetro de la base.
: Perímetro de la base.
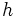 : altura.
: altura.

