Rectas de regresión (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Recta de regresión de Y sobre X
Consideremos una variable bidimensional 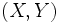 y una serie de valores observados
y una serie de valores observados 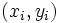 que representamos en el plano mediante una nube de puntos. Buscamos la recta que mejor se ajuste a la nube. Para ello utilizaremos el método de mínimos cuadrados que consiste en quedarse con aquella recta que cumpla que "la suma de los cuadrados de las distancias de todos los puntos a la recta sea mínima". Así se obtiene:
que representamos en el plano mediante una nube de puntos. Buscamos la recta que mejor se ajuste a la nube. Para ello utilizaremos el método de mínimos cuadrados que consiste en quedarse con aquella recta que cumpla que "la suma de los cuadrados de las distancias de todos los puntos a la recta sea mínima". Así se obtiene:
Recta de regresión de Y sobre X
La recta de regresión de Y sobre X viene dada por la ecuación:
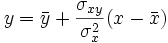
Es una recta que pasa por el centro de gravedad de la nube 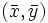 y cuya pendiente,
y cuya pendiente, 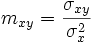 , recibe el nombre de coeficiente de regresión.
, recibe el nombre de coeficiente de regresión.
La demostración excede el nivel de este curso.
Nota: El coeficiente de regresión y el de correlación coinciden en signo. No obstante, no existe otra relación entre ambos coeficientes ya que, por ejemplo, la pendiente de la recta puede ser grande pero la correlación entre las variables ser baja.
Rectas de regresión de Y sobre X y de X sobre Y.
Determina las rectas de regresión de Y sobre X y de X sobre Y para una muestra de tamaño 9.
Determina las rectas de regresión de Y sobre X y de X sobre Y para una muestra de tamaño 10.
Posición relativa de las rectas de regresión:
- Si r=1, las dos rectas de regresión son coincidentes.
- Si r=0, la rectas de regresión son rectas perpendiculares iguales a las medias de las respectivas variables unidimensionales. Es decir:
- Recta de regresión de Y sobre X:
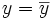
- Recta de regresión de X sobre Y:
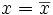
Estimaciones usando la recta de regresión
- Llamaremos valor estimado de
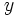 correspondiente a un valor dado
correspondiente a un valor dado 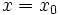 , al valor de
, al valor de 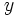 que se obtiene al sustituir en la recta de regresión la
que se obtiene al sustituir en la recta de regresión la 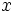 por
por 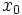 . Lo representaremos por
. Lo representaremos por 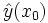
- Llamaremos valor estimado de
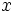 correspondiente a un valor dado
correspondiente a un valor dado 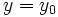 , al valor de
, al valor de 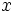 que se obtiene al sustituir en la recta de regresión la
que se obtiene al sustituir en la recta de regresión la 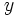 por
por 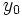 . Lo representaremos por
. Lo representaremos por 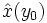
Algunas consideraciones:
- No olvidemos que éstos son valores estimados, es decir, que tienen una cierta probabilidad de que tomen ese valor.
- Estas estimaciones funcionan mejor cuando los valores de
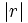 son próximos a 1 y cuando los valores de
son próximos a 1 y cuando los valores de 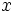 o de
o de 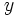 son próximos o están dentro del intervalo de los puntos de la nube.
son próximos o están dentro del intervalo de los puntos de la nube.
- Determina la recta de regresión de Y sobre X correspondiente a una muestra 50 empresas en las que se ha observado el número de trabajadores , "X", y la producción, "Y".
- Estima la producción de sendas empresas con 45 y 72 trabajadores, respectivamente.
- Determina la recta de regresión de Y sobre X.
- Estima el valor de "X" si Y=4 y si Y=11.
Recta de regresión. Estimación.
|
Actividad Interactiva: Recta de regresión de distribuciones bidimensionales. Estimación
(X,Y)=(Matemáticas,Física)={(3,2),(2,2),(5,6),(1,3),(7,6),(6,8),(2,4),(4,4),(8,10),(9,6),(5,7),(10,9),(7,7)}
(X,Y)=(Distancia, Hoyos)={(1,10),(2,10),(4,8),(6,7),(8,6),(10,3),(12,4),(15,3),(18,1),(20,0)} |
Apéndice
- Varianza resisual y varianaza explicada por la regresión.
- Coeficiente de determinación.
Implementación del cálculo del coeficiente de determinación con Excel.

