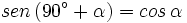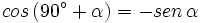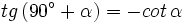Relaciones entre las razones trigonométricas de algunos ángulos (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
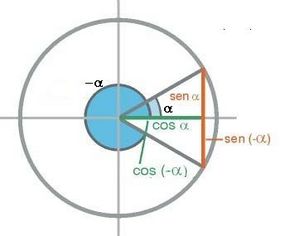
Ángulos opuestos
En esta escena podrás ver la relación entre las razones trigonométricas de ángulos opuestos.
Videotutorial.
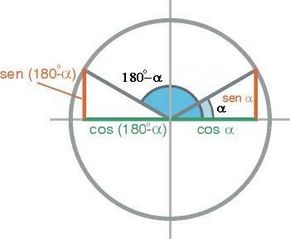
Ángulos suplementarios
En esta escena podrás ver la relación entre las razones trigonométricas de ángulos suplementarios.
Videotutorial.
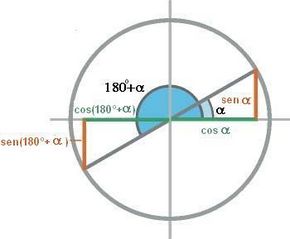
Ángulos que difieren en 180º
Razones trigonométricas de ángulos que difieren en 180º
En esta escena podrás ver la relación entre las razones trigonométricas de ángulos que difieren en 180º.
Videotutorial.
Ángulos complementarios
En esta escena podrás ver la relación entre las razones trigonométricas de ángulos complementarios.
Videotutorial.
Videotutorial.
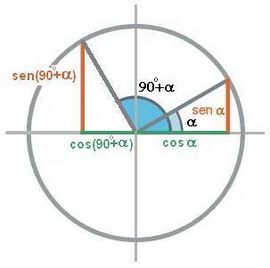
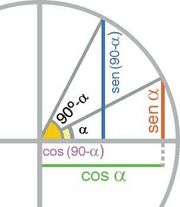
Ángulos que difieren en 90º
En esta escena podrás ver la relación entre las razones trigonométricas de ángulos que difieren en 90º.
Videotutorial.
Actividades
Ejercicio resuelto: Relaciones entre las razones trigonométricas de algunos ángulos
Sabiendo que:
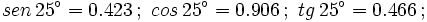
calcula todas las razones trigonométricas de:
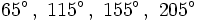
Utiliza que:
- 25º y 65º son complementarios.
- 25º y 115º se diferencian en 90º.
- 25º y 155º son suplementarios.
- 25º y 205º se diferencian en 180º.
Practica con las relaciones entre las razones trigonométricas de algunos ángulos y ponte a prueba con una autoevaluación.
- Si pulsas el botón "EJERCICIO" cambiarán los datos del problema.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
Relaciones entre las razones trigonométricas de algunos ángulos especiales.
Nota: Algunos ángulos vienen dados en radianes.
Cómo reducir ángulos al primer cuadrante. Ejemplos.
- Cómo reducir ángulos al primer cuadrante. Ejemplos en radianes.
- Nota: Si quieres aprender a pasar de radianes a grados sexagesimales pincha en el siguiente enlace: Medida de ángulos: el radián (1ºBach)
Reducción de ángulos al primer cuadrante:
- Deducción de las razones trigonométricas de
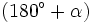 ,
, 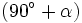 y
y 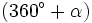 .
.
- Ejercicios: Calcula reduciendo al primer cuadrante:
- 1)
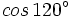
- 2)
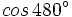
- 3)
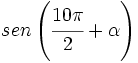
- 1) Sabiendo que
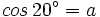 , halla el valor de:
, halla el valor de:
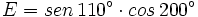
- 2) Sabiendo que
 e
e  son ángulos suplementarios y que
son ángulos suplementarios y que  es agudo, calcula:
es agudo, calcula:
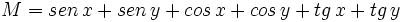
Simplifica:
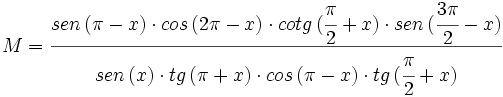
Ejercicios propuestos
|
Ejercicios propuestos: Relaciones entre las razones trigonométricas de algunos ángulos |
 un ángulo y
un ángulo y 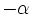 su opuesto.
su opuesto.
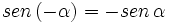
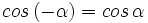
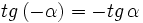
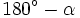 su suplementario.
su suplementario.
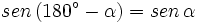
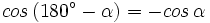
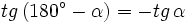
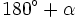 su opuesto por el vértice.
su opuesto por el vértice.
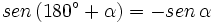
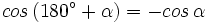
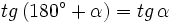
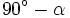 su complementario.
su complementario.
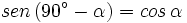
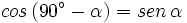
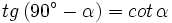
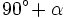 .
.