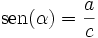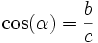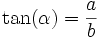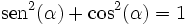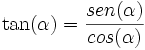Relaciones trigonométricas (PACS)

De Wikipedia

Tabla de contenidos 1 Trigonometría 2 Razones trigonométricas en un triángulo rectángulo 2.1 Ejemplo 3 Identidades fundamentales 4 Utilización de la calculadora en trigonometría

Trigonometría

La trigonometría en principio es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos. En términos generales, la trigonometría es el estudio de las funciones seno, coseno, tangente, cotangente, secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

Razones trigonométricas en un triángulo rectángulo

El un triángulo rectángulo, las razones trigonométricas del ángulo con vértice en A, son:

El seno: la razón entre el cateto opuesto y la hipotenusa:

El coseno: la razón entre el cateto adyacente y la hipotenusa:

La tangente: la razón entre el cateto opuesto y el adyacente:

Ejemplo

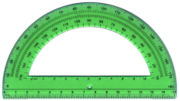
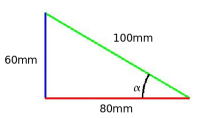
Tenemos un triángulo como el de la figura y queremos saber sus razones trigonométricas así que medimos sus tres lados a= 60mm b= 80mm c= 100mm

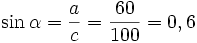
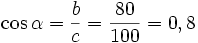
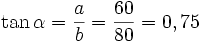
Identidades fundamentales

Una identidad es una igualdad en que se cumple para todos los valores permisibles de la variable:

Como en el triángulo rectángulo se cumple que a² + b² = c², de la figura anterior se tiene que sen α = a, cos α = b, c = 1; entonces para todo ángulo α, se cumple la identidad Pitagórica :

Además:

Utilización de la calculadora en trigonometría

Todas las calculadoras científicas del mercado disponen de teclas para las funciones trigonométricas seno, coseno y tangente. Sin embargo, es importante tener en cuenta dos factores de interés:

• En algunos modelos se introduce el valor del ángulo y luego se pulsa la tecla de la razón trigonométrica para obtener su valor, mientras que en otros se hace justamente al revés, primero se pulsa la tecla de la razón deseada, luego se introduce el valor del ángulo y por último la tecla de resultado (generalmente =) nos muestra el resultado en la pantalla.
• Las calculadoras científicas utilizan tres sistemas de medida angular, los radianes (RAD), los grados sexagesimales (DEG) y los gradianes (GRAD). Es muy importante tener en cuenta este factor, ya que no es lo mismo sin(100^o) = 0,984807753 que sin(100rad) = − 0,506365641 o sin(100gra) = 1. La conversión entre los sistemas es la siguiente: 180^o = πrad = 200gra