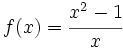Representación de funciones racionales (2ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
[editar]
Estudio y representación gráfica de funciones racionales
Procedimiento
En el estudio y representación gráfica de una función racional, 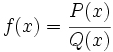 ,tendremos que determinar los siguientes apartados:
,tendremos que determinar los siguientes apartados:
- Dominio:
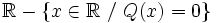 .
.
- Puntos de corte: Los puntos de corte con el eje X se obtienen resolviendo la ecuación f(x)=0, para lo que tendremos que resolver la ecuación polinómica P(x)=0 usando las técnicas vistas en temas anteriores. El punto de corte con el eje Y se obtiene calculando f(0).
- Signo de f(x): para el estudio del signo usaremos los puntos de corte y los puntos de discontinuidad, que son los puntos donde se anula el denominador, es decir, donde Q(x)=0.
- Puntos singulares de f(x) que se obtienen resolviendo la ecuación f '(x)=0. Por tanto, tendremos que resolver otra ecuación polinómica.
- Intervalos de crecimiento y decrecimiento de f(x): a partir de los puntos singulares y estudiando el signo de f '(x). Así podremos determinar los máximos y mínimos relativos de f(x).
- Intervalos de concavidad y puntos de inflexión de f(x): estudiando el signo de f "(x).
- Asíntotas y ramas infinitas:
- A.V.: Son "candidatos" a asíntota vertical los puntos donde Q(x)=0. Habrá que estudiar el límite de f(x) cuando x tiende a esos puntos candidatos. Aquellos para los que ese límite sea + o - infinito serán puntos con A.V.
- A.H.: Cuando el grado de Q(x) sea mayor o igual que el grado de P(x) tendremos asíntota horizontal.
- A.O.: Cuando el grado de P(x) sea igual al grado de Q(x) más uno, tendremos asíntota oblicua.
- Cuando no haya A.H. ni A.O. tendremos ramas infinitas.
- Simetrías: ver si f(x) es par o impar.
Ejercicios resueltos: Estudio y representación gráfica de funciones racionales
Estudia y representa:
- a)
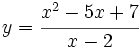 .
.
- b)
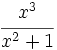 .
.
- c)
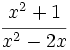 .
.
Solución:
Utiliza la siguiente escena para comprobar los resultados.
En la siguiente escena puedes ver la representación gráfica de distintas funciones.
Tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos.
Representación gráfica de 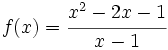
Representación gráfica de 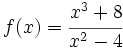
Estudio de las simetrías de:
a) 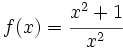
b)