Tablas de frecuencia bidimensionales (1ºBach)
De Wikipedia
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Tablas de correlación
Al igual que se hacía con las variables unidimensionales, que cuando el número de valores observados de la variable era grande, en vez de enumerarlos se construía una tabla de frecuencias, cuando trabajamos con variables bidimensionales, si el número de pares (x,y) observados es grande, en vez de enumerarlos se recurre a una tabla de frecuencias de doble entrada en la que cada celda contiene el número de veces que se observa cada pareja de valores (x,y).
Consideremos una población de 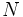 individuos sobre los que medimos conjuntamente dos variables,
individuos sobre los que medimos conjuntamente dos variables, 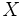 e
e 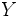 . Para cada individuo tendremos un par de valores observados
. Para cada individuo tendremos un par de valores observados 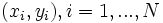 .
Al igual que en el caso unidimensional, debemos buscar una forma organizada de presentar las observaciones.
.
Al igual que en el caso unidimensional, debemos buscar una forma organizada de presentar las observaciones.
Supongamos que la variable 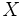 presenta
presenta 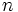 valores distintos,
valores distintos,  , y la variable
, y la variable 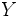 presenta
presenta 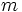 valores distintos,
valores distintos,  . Sea
. Sea 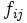 la frecuencia absoluta del par
la frecuencia absoluta del par 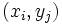 , es decir, el número de individuos que presentan el valor
, es decir, el número de individuos que presentan el valor 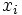 en el caracter
en el caracter 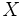 e
e 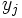 en el caracter
en el caracter 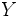 .
La tabla de correlación se construye colocando estas frecuencias en una tabla de doble entrada llamada tabla de correlación.
.
La tabla de correlación se construye colocando estas frecuencias en una tabla de doble entrada llamada tabla de correlación.
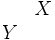 | 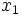 | 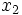 |  | 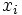 |  | 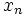 | 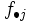
|
|---|---|---|---|---|---|---|---|
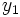 | 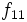 | 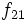 |  | 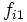 |  | 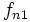 | 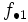
|
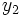 | 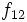 | 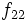 |  | 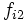 |  | 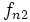 | 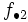
|
 |  |  |  |  |  |  | 
|
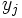 | 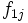 | 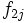 |  | 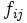 |  | 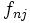 | 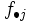
|
 |  |  |  |  |  |  | 
|
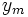 | 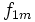 | 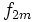 |  | 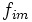 |  | 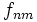 | 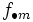
|
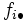 | 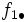 | 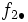 |  | 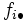 |  | 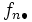 | 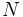
|
Distribuciones marginales
Se llama distribución marginal de la variable 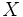 , a la distribución unidimensional formada por los valores
, a la distribución unidimensional formada por los valores 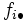 que se obtiene al sumar para cada valor
que se obtiene al sumar para cada valor 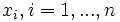 toda la columna de frecuencias
toda la columna de frecuencias 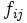 , es decir, es la formada a partir de los valores a última fila de la tabla anterior. Análogamente, la distribución marginal de la variable
, es decir, es la formada a partir de los valores a última fila de la tabla anterior. Análogamente, la distribución marginal de la variable 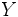 es la distribución unidimensional formada por los valores
es la distribución unidimensional formada por los valores 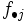 que se obtiene al sumar para cada valor
que se obtiene al sumar para cada valor 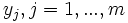 toda la fila de frecuencias
toda la fila de frecuencias 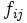 , es decir, es la formada a partir de la última columna de la tabla anterior.
, es decir, es la formada a partir de la última columna de la tabla anterior.
Frecuencias marginales
Se llaman frecuencias marginales de la variable 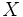 a los valores:
a los valores:
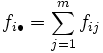 para
para 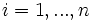 .
.
Analogamente tenemos las frecuencias marginales de 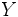 , que son los valores:
, que son los valores:
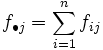 para
para 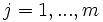 .
.
Media y desviación típica de las distribuciones marginales
Media de las distribuciones marginales
La media de la distribución marginal de 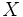 viene dada por:
viene dada por:
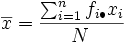
y la de 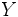 por:
por:
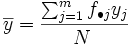
Desviación típica de las distribuciones marginales
La desviación típica de la distribución marginal de 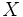 viene dada por:
viene dada por:
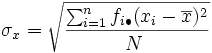
y la de 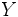 por:
por:
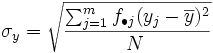
Videotutoriales
Videotutorial
Videotutorial

