Valor absoluto de una función (1ºBach)
De Wikipedia
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
[editar]
Función valor absoluto
La función valor absoluto es aquella que a cada número 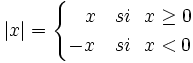 Representación de la función valor absoluto. |
[editar]
Valor absoluto de una función
El valor absoluto de una función se define como:
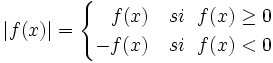
Siendo "f" y "u" funciones reales de variable real, escribimos f = | u | si f(x) = | u(x) | .
- La gráfica de "f" coincide con la de "u" en los puntos en que ésta toma valores no negativos.
- En los puntos en que "u" toma valores negativos, la gráfica de "f" es simétrica de la de "u" respecto al eje de abcisas.
Representación conjunta de una función cualquiera y su valor absoluto.
[editar]
Representación gráfica del valor absoluto de una función
Procedimiento
Para representar gráficamente el valor absoluto de una función f:
- Representamos la función f.
- Hacemos una simetría respecto del eje X de la parte de la gráfica de f que está por debajo de dicho eje.
- Borramos esa parte de f que está por debajo del eje X.
- La parte de la gráfica de f que está por encima del eje X la dejamos tal cual.
- La gráfica resultante es la gráfica del valor absoluto de f.
Representa gráficamente:
- a)
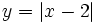
- b)
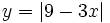
- c)
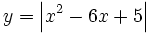
Representa gráficamente:
- a)
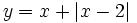
- b)
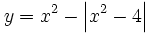
Representa gráficamente: 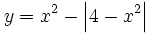
Representa gráficamente:
- a) f(x) = x + | x − 2 |
- b)
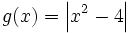
- c) h(x) = | x | − x
- d)
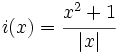
- e)
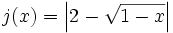
Autoevaluación.
 le asigna su
le asigna su