Variables aleatorias

De Wikipedia

Menú:

Ir a	Para repasar	Para ampliar	Enlaces externos
Indice Casio	Presentación		WIRIS Calculadora Descartes Variables aleatorias continuas

Tabla de contenidos

1 Definición
2 Variables aleatorias discretas
- 2.1 Distribución de probabilidades
- 2.2 Parámetros de una distribución discreta
3 Variables aleatorias continuas
- 3.1 Función de densidad
- 3.2 Media y Varianza
4 Ejemplos variables aleatorias

[editar]

Definición

Se llama variable aleatoria a toda aplicación $X$ del espacio muestral $E$ en un subconjunto de los numeros reales:

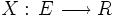
$X: \, E \longrightarrow R$
Al conjunto de valores de

R

asignados a los elementos de

E

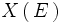se le llama recorrido de la variable aleatoria y se representa por $X \left( \, E \, \right)$ .

Una variable aleatoria es un valor numérico que corresponde al resultado de un experimento aleatorio, como la suma de los puntos obtenidos al lanzar dos dados, el número de lanzamientos de un dado hasta que aparece el cuatro, el número de personas que suben en un determinado ascensor al mes, el tiempo de espera en la sala de un doctor...

Las variables aleatorias discretas son aquellas que pueden tomar solamente un número finito o un número infinito numerable de valores.

A este nivel, las unicas variables aleatorias que consideraremos son aquellas que toman un número finito de valores. Un ejemplo de este tipo de variable aleatoria seria el resultado de lanzar un dado.

Las variables aleatorias continuas son aquellas que pueden tomar cualquier valor en un intervalo de la recta real. Un ejemplo de este tipo de variable aleatoria seria la altura de una persona.

[editar]

Variables aleatorias discretas

[editar]

Distribución de probabilidades

La distribución de probabilidad de una variable aleatoria discreta X asocia a cada uno de los valores que puede tomar X su probabilidad correspondiente.

Se lanzan tres monedas perfectas, entonces cada uno de los sucesos elementales del espacio muestral tiene probabilidad 1/8. La distribución de probabilidad de la variable aleatoria X =número de caras al tirar 3 monedas será:

$x i$	$P (X = x i)$
0	1/8
1	3/8
2	3/8
3	1/8

Algunas probabilidades con esta variable:

a) P(X = 0) + P(X = 1 ) + P(X = 2) + P(X = 3) = 1

b) P(1 < X 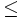$\le$ 3) = P(X = 2) + P(X = 3) = 3/8 + 1/ 8 = 1/2

c) P(X > 2) = P(X = 3) = 1/8

d) P(X > 1,5) = P(X = 2) + P(X = 3) = 3/8 + 1/ 8 = 1/2

[editar]

Parámetros de una distribución discreta

$μ$ : media o esperanza. Proporciona cuál es el valor promedio de la distribución.

$σ$ : desviación típica. Dispersión de los valores de X respecto a ese valor promedio.

Al realizar un experimento n veces, sean $x 1, x 2, x 3,....., x k$ los distintos valores de X ya sean 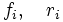$f_i ,\quad r_i$ las frecuencias absolutas y relativas de $x i$ . Si n es grande las frecuencias relativas se estabilizan en torno a las probabilidades $P (x i)$ y se tiene:

[editar]

Variables aleatorias continuas

Para una variable aleatoria continua X, sobre una población muy grande, con una muestra de tamaño n construimos el histograma en escala de densidad. En estos histogramas:

- Los intervalos de clase son de igual amplitud.

- La superficie encerrada por cada rectángulo es igual a la frecuencia relativa correspondiente al intervalo.

- Por tanto la suma de las áreas de todos los rectángulos es 1.

Al hacer que n (tamaño de la muestra) crezca, y la amplitud de los intervalos disminuya observamos que la curva se aproxima a una curva f que se denomina función de densidad de la variable X.