Brahmagupta
De Wikipedia
| Revisión de 20:29 24 dic 2008 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Astronomía) |
||
| Línea 7: | Línea 7: | ||
| Aunque Brahmagupta estaba familiarizado con las obras de los astrónomos siguiendo la tradición de Aryabhatiya, no se sabe si está familiarizado con la labor de Bhaskara I, un contemporáneo. Brahmagupta tenía una cantidad de críticas dirigidas hacia la labor de los astrónomos rivales, y en su ''Brahmasphutasiddhanta'' se encuentra uno de los primeros cismas de fe entre matemáticos indios. La división fue principalmente sobre la aplicación de las matemáticas al mundo físico, más que sobre las matemáticas en si mismas. En el caso de Brahmagupta, los desacuerdos se debieron en gran parte de la elección de las teorías y parámetros astronómicos. A lo largo de los primeros diez capítulos astronómicos aparecen críticas a las teorías rivales, y el undécimo capítulo está completamente dedicado a la crítica de estas teorías, aunque las críticas no aparecen en el duodécimo y décimo octavo capítulos. | Aunque Brahmagupta estaba familiarizado con las obras de los astrónomos siguiendo la tradición de Aryabhatiya, no se sabe si está familiarizado con la labor de Bhaskara I, un contemporáneo. Brahmagupta tenía una cantidad de críticas dirigidas hacia la labor de los astrónomos rivales, y en su ''Brahmasphutasiddhanta'' se encuentra uno de los primeros cismas de fe entre matemáticos indios. La división fue principalmente sobre la aplicación de las matemáticas al mundo físico, más que sobre las matemáticas en si mismas. En el caso de Brahmagupta, los desacuerdos se debieron en gran parte de la elección de las teorías y parámetros astronómicos. A lo largo de los primeros diez capítulos astronómicos aparecen críticas a las teorías rivales, y el undécimo capítulo está completamente dedicado a la crítica de estas teorías, aunque las críticas no aparecen en el duodécimo y décimo octavo capítulos. | ||
| - | Seguir traducción de http://en.wikipedia.org/wiki/Brahmagupta | + | == Matemáticas == |
| + | La obra más famosa de Brahmagupta es su ''Brahmasphutasiddhanta''. Compuesta en verso elíptico, practica común en las matemáticas indueshematics]], la obra tiene, en consecuencia, un cierto halo poético. Como en ella no se dan demostraciones, no se sabe como Brahmagupta obtenía los resultados matemáticos. | ||
| + | |||
| + | ===Algebra === | ||
| + | Brahmagupta da la solución de la '''ecuación lineal general''' en el capítulo dieciocho de ''Brahmasphutasiddhanta'', que aunque expresada en el libro en palabras, viene a ser equivalente a la siuiente expresión algebraica: | ||
| + | |||
| + | <center><math>x = \frac{e-c}{b-d}</math></center> | ||
| + | |||
| + | Además, dio dos soluciones equivalentes para la '''ecuación general de segundo grado''', que vienen a ser equivalentes, respectivamente, a las siguientes expresiones algebraicas: | ||
| + | |||
| + | <center><math>x = \frac{\sqrt{4ac+b^2}-b}{2a} </math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>x = \frac{\sqrt{ac+\frac{b^2}{4}}-\frac{b}{2}}{a} </math></center> | ||
| + | |||
| + | El contina resolviendo sistemas de ecuaciones indeterminados, enunciando que la variable elegida debe primero aislarse, y que luego la ecuación debe dividirse por el coeficiente de la variable elegida. | ||
| + | |||
| + | Al igual que el álgebra de [[Diofanto]], el álgebra de Brahmagupta es sincopada. La suma la indicaba colocando los números uno al lado del otro, la resta colocando un punto sobre el sustraendo, la división colocando el divisor debajo del dividendo, similar a nuestra notación, pero sin la barra. La multiplicación, las raices y las incógnitas las representaba mediante abrebiaturas de términos apropiados. | ||
| + | Fue el primero en dar una solución general a la '''ecuación lineal de Diofanto''' <math>ax + by = c</math>, donde a, b, y c son enteros. También es muy posible que diese todas las soluciones de dicha ecuación, mientras que Diofanto se sintió satisfecho con dar una sola solución de una ecuación indeterminada. En la medida en que Brahmagupta utilizó algunos ejemplos iguales a los de Diofanto, vemos la posibilidad de que ambos hubiesen usado las mismas fuentes, posiblemente babilónicas. No se sabe hasta que punto el uso de la notación sincopada en el álgebra de Brahmagupta es debido a los griegos o si tanto griegos como hindues derivan su uso de una fuente común usase notación sincopada, no se conoce y es posible que tanto el griego y el indio síncopa pueden derivarse de una fuente común, las matemáticas babilónicas. | ||
| + | |||
| + | ===Aritmética=== | ||
| + | *'''Fracciones:''' Al comienzo del capítulo doce de su ''Brahmasphutasiddhanta'', titulado ''Cálculo'', Brahmagupta detalla operaciones con fracciones. Da por supuesto que el lector conoce las operaciones aritméticas básicas, como tomar la raíz cuadrada, aunque si explica cómo hallar el cubo y la raíz cúbica de un número entero y, posteriormente, da normas que facilitan el cálculo de cuadrados y raíces cuadradas. A continuación, da las normas para abordar cinco tipos de combinaciones de fracciones, | ||
| + | |||
| + | <center><math>\cfrac{a}{c} + \cfrac{b}{c}</math>;{{b}} <math>\cfrac{a}{c} \cdot \cfrac{b}{d}</math>;{{b}} <math>\cfrac{a}{1} + \cfrac{b}{d}</math>;{{b}} <math>\cfrac{a}{c} + \cfrac{b}{d} \cdot \cfrac{a}{c} = \cfrac{a(d+b)}{cd}</math>;{{b}} <math>\cfrac{a}{c} - \cfrac{b}{d} \cdot \cfrac{a}{c} = \cfrac{a(d-b)}{cd}</math></center> | ||
| + | |||
| + | *'''Series:''' | ||
| + | Brahmagupta continua dando la suma de los cuadrados y los cubos de los primeros "n" enteros. Traduciendo algebraicamente sus palabras sería: | ||
| + | |||
| + | #Suma de los cuadrados de los n primeros números naturales: <math>n\cdot(n+1)\cdot \frac{2n+1}{6}</math> | ||
| + | #Suma de los cubos de los n primeros números naturales:<math>\left( \cfrac {n\cdot(n+1)}{2} \right)^2</math>. | ||
| + | |||
| + | *'''El cero y los números negativos:''' | ||
| + | Brahmagupta hace uso del '''número cero''' en su ''Brahmasphutasiddhanta'', siendo este el primer texto conocido en el cual se trata al cero con entidad propia, más que como un simple dígito usado para representar otros números, como hacían los babilonios, o como símbolo para indicar la carencia de una cantidad, como hacía Ptolomeo y los romanos. En el capítulo octavo de ''Brahmasphutasiddhanta'', Brahmagupta describes operaciones con '''númeroas negativos'''. Primero describe la suma y la resta, luego prosigue con la multiplicación dando una correcta regla de los signos, pero al dar la división lo estropea permitiendo la división por cero. Brahmagupta, por ejemplo, dice que: <math>\frac{0}{0} = 0</math> | ||
| + | |||
| + | ===Análisis diofántico=== | ||
| + | *'''Ternas pitagóricas:''' En el capítulo doce de ''Brahmasphutasiddhanta'', Brahmagupta halla ternas pitagóricas. Expresandolo en términos algebraicos: | ||
| + | Para una longitud dada <math>m\;</math> y un multiplicador arbitrario <math>x\;</math>, sean <math>a=mx\;</math> y <math>b=m+ \cfrac{mx}{(x + 2)}</math>. Entonces <math>m\;</math>, <math>a\;</math>, y <math>b\;</math> forman una terna pitagórica. | ||
| + | |||
| + | *'''Ecuación de Pell:''' Brahmagupta da una relación de recurrencia para generar soluciones de ciertos tipos de ecuaciones diofánticas de segundo grado, tales como <math>Nx^2 + 1 = y^2</math> (llamada ecuación de Pell), usando el algoritmo de [[Euclides]]. El algoritmo de Euclides le era conocido con el nombre de "pulverizador" ya que simplificaba los números. | ||
| + | |||
| + | La clave para su solución era la identidad: | ||
| + | |||
| + | <center><math>(x^2_1 - Ny^2_1)(x^2_2 - Ny^2_2) = (x_1 x_2 + Ny_1 y_2)^2 - N(x_1 y_2 + x_2 y_1)^2</math></center> | ||
| + | |||
| + | que es una generalización de una identidad descubierta por [[Diofanto]], | ||
| + | |||
| + | <center><math>(x^2_1 - y^2_1)(x^2_2 - y^2_2) = (x_1 x_2 + y_1 y_2)^2 - (x_1 y_2 + x_2 y_1)^2.</math></center> | ||
| + | |||
| + | Usando esta identidad y el hecho de que si<math>(x_1,</math> <math>y_1)\;</math> and <math>(x_2,\;</math> <math>y_2)\;</math> son soluciones de las ecuaciones <math>x^2 - Ny^2 = k_1\;</math> y <math>x^2 - Ny^2 = k_2\;</math>, respectivamente, entonces <math>(x_1 x_2 + N y_1 y_2,\;</math> <math>x_1 y_2 + x_2 y_1)\;</math> es una solución de <math>x^2 - Ny^2 = k_1 k_2\;</math>, él supo encontrar soluciones enteras de la ecuación de Pell equation mediante una serie de ecuaciones de la forma <math>x^2 - Ny^2 = k_i\;</math>. Por desgracia, Brahmagupta no fue capaz de aplicar su solución de forma uniforme para todos los posibles valores de ''N'', sino que sólo pudo demostrar que si <math>x^2 - Ny^2 = k\;</math> tiene una solución entera para <math>k = \pm 1, \pm 2, \pm 4</math>, entonces <math>x^2 - Ny^2 = 1\;</math> tiene una solución. la solución de la ecuación general de Pell tendría que esperar a [[Bhaskara II]] (c. 1150) | ||
| + | |||
| + | ===Geometría === | ||
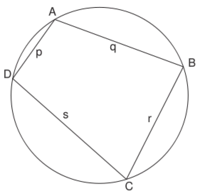
| + | *'''Fórmula de Brahmagupta:''' El resultado en geometría más famoso de Brahmagupta es su fórmula para los cuadriláteros cíclicos (aquellos inscritos en una circunferencia). | ||
| + | [[Image:Cuadrilatero_ciclico.png|200px|thumb|right|Cuadrilátero cíclico]] | ||
| + | Dadas las longitudes de los lados de un cuadrilátero cíclico cualquiera, Brahmagupta dió una fórmula aproximada y otra exacta para el área de dicha figura. la traducción algebraica diría: Dadas las longitudes <math>p\;</math>, <math>q\;</math>, <math>r\;</math> y <math>s\;</math> de un cuadrilátero cíclico, | ||
| + | |||
| + | *Area aproximada: <math>A=(\cfrac{p + r}{2}) (\cfrac{q + s}{2})</math> | ||
| + | *Area exacta:<math>\sqrt{(t - p)(t - q)(t - r)(t - s)}</math>, donde <math>t = \cfrac{p + q + r + s}{2}</math>. | ||
| + | |||
| + | Aunque Brahmagupta no enuncia explícitamente que se trate de cuadriláteros cíclicos, parece deducirse de sus reglas que ese es el caso. | ||
| + | |||
| + | La '''fórmula de [[Heron]]''' se obtiene como caso particular de la de Brahmagupta, haciendo uno de los lados igual a cero. | ||
| + | |||
| + | *'''Triángulos:''' Uno de los teoremas en la obra de Brahmagupta dice que las medidas de los dos segmentos en que la altura de un triángulo divide a la base son: | ||
| + | <center><math>b \pm \cfrac{c^2 - a^2}{b}</math></center> | ||
| + | |||
| + | Además da un teorema sobre triángulos racionales (cuyos lados son números racionales): | ||
| + | Un triángulo con lados racionales <math>a\;</math>, <math>b\;</math> y <math>c\;</math> y área racional es de la forma: | ||
| + | |||
| + | <center><math>a = \frac{1}{2}\left(\frac{u^2}{v}+v\right), \ \ b = \frac{1}{2}\left(\frac{u^2}{w}+w\right), \ \ c = \frac{1}{2}\left(\frac{u^2}{v} - v + \frac{u^2}{w} - w\right) </math></center> | ||
| + | |||
| + | para algunos racionales <math>u\;</math>, <math>v\;</math>, y <math>w\;</math>. | ||
| + | |||
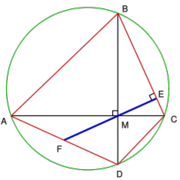
| + | *Teorema de Brahmagupta: | ||
| + | [[Image:Brahmagupta_teorema.png|thumb|right|El teorema de Brahmagupta dice que ''AF'' = ''FD''.]] | ||
| + | Brahmagupta continua diciendo que, en un cuadrilátero cíclico "no desigual" (trapezoide equilatero), la longitud de las diagonales es: | ||
| + | <center><math>\sqrt{pr + qs}</math></center> | ||
| + | Sigue dando las fórmulas de las longitudes y áreas de figuras geométricas como la medida del radio de la circunferencia circunscrita al trapezoide isósceles y del cuadrilátero escaleno, y las medidas de las diagonales de un cuadrilátero cíclico escaleno. Esto lleva al famoso teorema de Brahmagupta. (ver dibujo adjunto) | ||
| + | |||
| + | *'''Pi:''' En el verso 40, da valores del número Pi: 3 como valor práctico de Pi y <math>\sqrt{10}</math> como valor más preciso. | ||
| + | |||
| + | *'''Medidas y construcciones:''' | ||
| + | En algunos de los versos anteriores al 40, Brahmagupta da la construcción de varias figuras con lados arbitrarios. El manipuló esencialmente triángulos rectángulos para obtener trángulos isósceles, triángulos escalenos, rectángulos, trapezoides isósceles, trapezoides isósceles con tres lados iguales, y cuadriláteros cíclicos escalenos. | ||
| + | |||
| + | Tras dar el valor de Pi, trata aspectos de la geometría planas y de sólidos, como encontrar sus volúmenes y superficies. Halla el volumen de prismas rectos, pirámides, y troncos de pirámides de base cuadrada. | ||
| + | |||
| + | ===Trigonometría=== | ||
| + | En el capítulo 2 de ''Brahmasphutasiddhanta'', titulado ''Longitudes Planetarias Verdaderas'', Brahmagupta presenta una tabla de senos, usando nombres de objetos para representar los números, algo que era común en los tratatados en sanscrito. Así, por ejemplo, "Osa mayor" representa el 7 (por las 7 estrellas de dicha constelación), "gemelos" al 2, "Vedas" el 4 (por los 4 Vedas), Progenitores el 14, etc. esta información, traducida en números, da la lista de senos: 214 (gemelos, Progenitores), 427 (Osa Mayor, gemelos, Vedas), 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, y 3270, siendo el radio 3270. | ||
| + | |||
| + | ==Astronomía== | ||
| + | Fue a traves de el ''Brahmasphutasiddhanta'' como los árabes aprendieron la astronomía hindú. El famoso califa abasida Al-Mansur (712–775), fundó Baghdad, situada a orillas del Tigris, e la hizo centro de aprendizaje. El califa invitó a un estudiante de Ujjain llamado Kankah en 770 a.C. Kankah usó el ''Brahmasphutasiddhanta'' para explicar el sistema hindú de astronomía aritmética. Muhammad al-Fazari tradujo el trabajo de Brahmugupta al árabe a demanda del califa. | ||
| + | |||
| + | En el capítulo siete de ''Brahmasphutasiddhanta'', titulado ''Creciente Lunar'', Brahmagupta refuta la idea de que la Luna se encuentra más alejada que el Sol de la Tierra, idea que se mantuvo en las escrituras. El hace ésto explicando la iluminación de la Luna por el Sol. También explicó que, como la Luna está más cerca de la Tierra que el Sol, la cantidad de parte iluminada de la Luna depende de la posición relativa del Sol y la Luna, y esto puede calcularse a partir del ángulo que forman los dos cuerpos. | ||
| + | |||
| + | Algunas de las aportaciones de importancia hechas por Brahmagupta a la astronomía son: métodos para calcular la posición de cuerpos celestes en el tiempo (efemérides), su aparición y su ocultación, conjunciones, y el cálculo de los eclipses solares y lunares. Brahmagupta criticó el punto de vista puránico de que la Tierra era plana o hueca. Por el contrario, observó que la Tierra y el cielo eran esféricos y que la Tierra se mueve. En el año 1030, el astrónomo musulmán, Abu al-Rayhan al-Biruni, en su ''Ta'rikh al-Hind'', posteriormente traducido al latín como ''Indica'', comentó el trabajo de Brahmaguptas y escribió que los críticos argumentaron: | ||
| + | |||
| + | "Si eso es así, las piedras y los árboles se caerían de la Tierra." | ||
| + | |||
| + | De acuerdo con al-Biruni, Brahmagupta respondió a estas críticas con el siguiente argumento sobre gravitación: | ||
| + | ... Todas las cosas pesadas son atraidas hacia el centro de la Tierra... La Tierra es igual por todos lados; todo el mundo sobre la Tierra permanece derecho, y todas las cosas pesadas caen a al Tierra por una ley de la naturaleza, porque está en la naturaleza de la Tierra atraer y mantener las cosas, como está en la naturaleza del agua fluir, en la del fuego quemar, y en la del viento mantenerse en movimientootion..." | ||
| [[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]] | [[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]] | ||
Revisión actual
Brahmagupta (598–668), matemático y astrónomo indú.
Tabla de contenidos |
Vida y obra
Brahmagupta nació en el año 598 en Bhinmal, ciudad en el estado de Rajasthan, al noroeste de la India. Probablemente vivió la mayor parte de su vida en Bhillamala (moderna Bhinmal, en Rajasthan) en el imperio de Harsha, durante el reinado del Rey Vyaghramukha. Como resultado de ello, Brahmagupta es a menudo citado como Bhillamalacarya que quiere decir, el maestro de Bhillamala Bhinmal.
Fue el jefe del observatorio astronómico en Ujjain, y durante su mandato allí escribió cuatro textos sobre las matemáticas y la astronomía: Cadamekela en el 624, Brahmasphutasiddhanta en 628, Khandakhadyaka en 665, y Durkeamynarda en 672. El Brahmasphutasiddhanta (Tratado corregido de Brahma) es posiblemente su obra más famosa. El historiador Al-Biruni (c. 1050) en su libro Tariq al-Hind, afirma que el califa Abbasid al-Ma'mun, que tenía una embajada en la India, llevó de3 allí un libro a Bagdad que fue traducido al árabe como Sindhind. Se presume que Sindhind no es otro que Brahmagupta-Brahmasphuta Siddhanta.
Aunque Brahmagupta estaba familiarizado con las obras de los astrónomos siguiendo la tradición de Aryabhatiya, no se sabe si está familiarizado con la labor de Bhaskara I, un contemporáneo. Brahmagupta tenía una cantidad de críticas dirigidas hacia la labor de los astrónomos rivales, y en su Brahmasphutasiddhanta se encuentra uno de los primeros cismas de fe entre matemáticos indios. La división fue principalmente sobre la aplicación de las matemáticas al mundo físico, más que sobre las matemáticas en si mismas. En el caso de Brahmagupta, los desacuerdos se debieron en gran parte de la elección de las teorías y parámetros astronómicos. A lo largo de los primeros diez capítulos astronómicos aparecen críticas a las teorías rivales, y el undécimo capítulo está completamente dedicado a la crítica de estas teorías, aunque las críticas no aparecen en el duodécimo y décimo octavo capítulos.
Matemáticas
La obra más famosa de Brahmagupta es su Brahmasphutasiddhanta. Compuesta en verso elíptico, practica común en las matemáticas indueshematics]], la obra tiene, en consecuencia, un cierto halo poético. Como en ella no se dan demostraciones, no se sabe como Brahmagupta obtenía los resultados matemáticos.
Algebra
Brahmagupta da la solución de la ecuación lineal general en el capítulo dieciocho de Brahmasphutasiddhanta, que aunque expresada en el libro en palabras, viene a ser equivalente a la siuiente expresión algebraica:
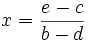
Además, dio dos soluciones equivalentes para la ecuación general de segundo grado, que vienen a ser equivalentes, respectivamente, a las siguientes expresiones algebraicas:
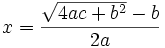
y
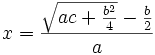
El contina resolviendo sistemas de ecuaciones indeterminados, enunciando que la variable elegida debe primero aislarse, y que luego la ecuación debe dividirse por el coeficiente de la variable elegida.
Al igual que el álgebra de Diofanto, el álgebra de Brahmagupta es sincopada. La suma la indicaba colocando los números uno al lado del otro, la resta colocando un punto sobre el sustraendo, la división colocando el divisor debajo del dividendo, similar a nuestra notación, pero sin la barra. La multiplicación, las raices y las incógnitas las representaba mediante abrebiaturas de términos apropiados. Fue el primero en dar una solución general a la ecuación lineal de Diofanto ax + by = c, donde a, b, y c son enteros. También es muy posible que diese todas las soluciones de dicha ecuación, mientras que Diofanto se sintió satisfecho con dar una sola solución de una ecuación indeterminada. En la medida en que Brahmagupta utilizó algunos ejemplos iguales a los de Diofanto, vemos la posibilidad de que ambos hubiesen usado las mismas fuentes, posiblemente babilónicas. No se sabe hasta que punto el uso de la notación sincopada en el álgebra de Brahmagupta es debido a los griegos o si tanto griegos como hindues derivan su uso de una fuente común usase notación sincopada, no se conoce y es posible que tanto el griego y el indio síncopa pueden derivarse de una fuente común, las matemáticas babilónicas.
Aritmética
- Fracciones: Al comienzo del capítulo doce de su Brahmasphutasiddhanta, titulado Cálculo, Brahmagupta detalla operaciones con fracciones. Da por supuesto que el lector conoce las operaciones aritméticas básicas, como tomar la raíz cuadrada, aunque si explica cómo hallar el cubo y la raíz cúbica de un número entero y, posteriormente, da normas que facilitan el cálculo de cuadrados y raíces cuadradas. A continuación, da las normas para abordar cinco tipos de combinaciones de fracciones,
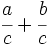 ;
; 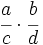 ;
; 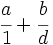 ;
; 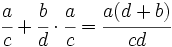 ;
; 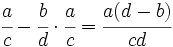
- Series:
Brahmagupta continua dando la suma de los cuadrados y los cubos de los primeros "n" enteros. Traduciendo algebraicamente sus palabras sería:
- Suma de los cuadrados de los n primeros números naturales:
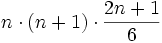
- Suma de los cubos de los n primeros números naturales:
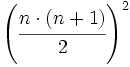 .
.
- El cero y los números negativos:
Brahmagupta hace uso del número cero en su Brahmasphutasiddhanta, siendo este el primer texto conocido en el cual se trata al cero con entidad propia, más que como un simple dígito usado para representar otros números, como hacían los babilonios, o como símbolo para indicar la carencia de una cantidad, como hacía Ptolomeo y los romanos. En el capítulo octavo de Brahmasphutasiddhanta, Brahmagupta describes operaciones con númeroas negativos. Primero describe la suma y la resta, luego prosigue con la multiplicación dando una correcta regla de los signos, pero al dar la división lo estropea permitiendo la división por cero. Brahmagupta, por ejemplo, dice que: 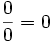
Análisis diofántico
- Ternas pitagóricas: En el capítulo doce de Brahmasphutasiddhanta, Brahmagupta halla ternas pitagóricas. Expresandolo en términos algebraicos:
Para una longitud dada  y un multiplicador arbitrario
y un multiplicador arbitrario  , sean
, sean 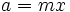 y
y 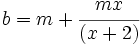 . Entonces
. Entonces  ,
,  , y
, y  forman una terna pitagórica.
forman una terna pitagórica.
- Ecuación de Pell: Brahmagupta da una relación de recurrencia para generar soluciones de ciertos tipos de ecuaciones diofánticas de segundo grado, tales como Nx2 + 1 = y2 (llamada ecuación de Pell), usando el algoritmo de Euclides. El algoritmo de Euclides le era conocido con el nombre de "pulverizador" ya que simplificaba los números.
La clave para su solución era la identidad:
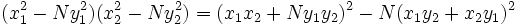
que es una generalización de una identidad descubierta por Diofanto,
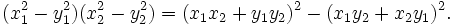
Usando esta identidad y el hecho de que si(x1,  and
and 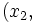
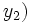 son soluciones de las ecuaciones
son soluciones de las ecuaciones 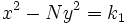 y
y 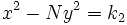 , respectivamente, entonces
, respectivamente, entonces 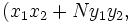
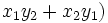 es una solución de
es una solución de 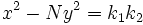 , él supo encontrar soluciones enteras de la ecuación de Pell equation mediante una serie de ecuaciones de la forma
, él supo encontrar soluciones enteras de la ecuación de Pell equation mediante una serie de ecuaciones de la forma 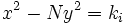 . Por desgracia, Brahmagupta no fue capaz de aplicar su solución de forma uniforme para todos los posibles valores de N, sino que sólo pudo demostrar que si
. Por desgracia, Brahmagupta no fue capaz de aplicar su solución de forma uniforme para todos los posibles valores de N, sino que sólo pudo demostrar que si 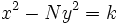 tiene una solución entera para
tiene una solución entera para 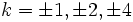 , entonces
, entonces 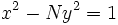 tiene una solución. la solución de la ecuación general de Pell tendría que esperar a Bhaskara II (c. 1150)
tiene una solución. la solución de la ecuación general de Pell tendría que esperar a Bhaskara II (c. 1150)
Geometría
- Fórmula de Brahmagupta: El resultado en geometría más famoso de Brahmagupta es su fórmula para los cuadriláteros cíclicos (aquellos inscritos en una circunferencia).
Dadas las longitudes de los lados de un cuadrilátero cíclico cualquiera, Brahmagupta dió una fórmula aproximada y otra exacta para el área de dicha figura. la traducción algebraica diría: Dadas las longitudes 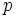 ,
, 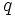 ,
,  y
y 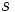 de un cuadrilátero cíclico,
de un cuadrilátero cíclico,
- Area aproximada:
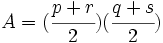
- Area exacta:
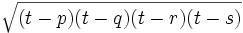 , donde
, donde 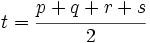 .
.
Aunque Brahmagupta no enuncia explícitamente que se trate de cuadriláteros cíclicos, parece deducirse de sus reglas que ese es el caso.
La fórmula de Heron se obtiene como caso particular de la de Brahmagupta, haciendo uno de los lados igual a cero.
- Triángulos: Uno de los teoremas en la obra de Brahmagupta dice que las medidas de los dos segmentos en que la altura de un triángulo divide a la base son:
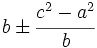
Además da un teorema sobre triángulos racionales (cuyos lados son números racionales):
Un triángulo con lados racionales  ,
,  y
y  y área racional es de la forma:
y área racional es de la forma:
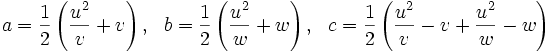
para algunos racionales 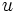 ,
, 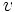 , y
, y 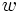 .
.
- Teorema de Brahmagupta:
Brahmagupta continua diciendo que, en un cuadrilátero cíclico "no desigual" (trapezoide equilatero), la longitud de las diagonales es:
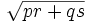
Sigue dando las fórmulas de las longitudes y áreas de figuras geométricas como la medida del radio de la circunferencia circunscrita al trapezoide isósceles y del cuadrilátero escaleno, y las medidas de las diagonales de un cuadrilátero cíclico escaleno. Esto lleva al famoso teorema de Brahmagupta. (ver dibujo adjunto)
- Pi: En el verso 40, da valores del número Pi: 3 como valor práctico de Pi y
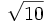 como valor más preciso.
como valor más preciso.
- Medidas y construcciones:
En algunos de los versos anteriores al 40, Brahmagupta da la construcción de varias figuras con lados arbitrarios. El manipuló esencialmente triángulos rectángulos para obtener trángulos isósceles, triángulos escalenos, rectángulos, trapezoides isósceles, trapezoides isósceles con tres lados iguales, y cuadriláteros cíclicos escalenos.
Tras dar el valor de Pi, trata aspectos de la geometría planas y de sólidos, como encontrar sus volúmenes y superficies. Halla el volumen de prismas rectos, pirámides, y troncos de pirámides de base cuadrada.
Trigonometría
En el capítulo 2 de Brahmasphutasiddhanta, titulado Longitudes Planetarias Verdaderas, Brahmagupta presenta una tabla de senos, usando nombres de objetos para representar los números, algo que era común en los tratatados en sanscrito. Así, por ejemplo, "Osa mayor" representa el 7 (por las 7 estrellas de dicha constelación), "gemelos" al 2, "Vedas" el 4 (por los 4 Vedas), Progenitores el 14, etc. esta información, traducida en números, da la lista de senos: 214 (gemelos, Progenitores), 427 (Osa Mayor, gemelos, Vedas), 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, y 3270, siendo el radio 3270.
Astronomía
Fue a traves de el Brahmasphutasiddhanta como los árabes aprendieron la astronomía hindú. El famoso califa abasida Al-Mansur (712–775), fundó Baghdad, situada a orillas del Tigris, e la hizo centro de aprendizaje. El califa invitó a un estudiante de Ujjain llamado Kankah en 770 a.C. Kankah usó el Brahmasphutasiddhanta para explicar el sistema hindú de astronomía aritmética. Muhammad al-Fazari tradujo el trabajo de Brahmugupta al árabe a demanda del califa.
En el capítulo siete de Brahmasphutasiddhanta, titulado Creciente Lunar, Brahmagupta refuta la idea de que la Luna se encuentra más alejada que el Sol de la Tierra, idea que se mantuvo en las escrituras. El hace ésto explicando la iluminación de la Luna por el Sol. También explicó que, como la Luna está más cerca de la Tierra que el Sol, la cantidad de parte iluminada de la Luna depende de la posición relativa del Sol y la Luna, y esto puede calcularse a partir del ángulo que forman los dos cuerpos.
Algunas de las aportaciones de importancia hechas por Brahmagupta a la astronomía son: métodos para calcular la posición de cuerpos celestes en el tiempo (efemérides), su aparición y su ocultación, conjunciones, y el cálculo de los eclipses solares y lunares. Brahmagupta criticó el punto de vista puránico de que la Tierra era plana o hueca. Por el contrario, observó que la Tierra y el cielo eran esféricos y que la Tierra se mueve. En el año 1030, el astrónomo musulmán, Abu al-Rayhan al-Biruni, en su Ta'rikh al-Hind, posteriormente traducido al latín como Indica, comentó el trabajo de Brahmaguptas y escribió que los críticos argumentaron:
"Si eso es así, las piedras y los árboles se caerían de la Tierra."
De acuerdo con al-Biruni, Brahmagupta respondió a estas críticas con el siguiente argumento sobre gravitación: ... Todas las cosas pesadas son atraidas hacia el centro de la Tierra... La Tierra es igual por todos lados; todo el mundo sobre la Tierra permanece derecho, y todas las cosas pesadas caen a al Tierra por una ley de la naturaleza, porque está en la naturaleza de la Tierra atraer y mantener las cosas, como está en la naturaleza del agua fluir, en la del fuego quemar, y en la del viento mantenerse en movimientootion..."