Brahmagupta

De Wikipedia

Revisión de 09:18 25 dic 2008 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior		Revisión actual Coordinador (Discusión | contribuciones) (→Astronomía)
Línea 29:		Línea 29:
	===Aritmética===		===Aritmética===
-	Al comienzo del capítulo doce de su''Brahmasphutasiddhanta'', titulado ''Cálculo'', Brahmagupta detalla operaciones con fracciones. Da por supuesto que el lector conoce las operaciones aritméticas básicas, como tomar la raíz cuadrada, aunque si explica cómo hallar el cubo y la raíz cúbica de un número entero y, posteriormente, da normas que facilitan el cálculo de cuadrados y raíces cuadradas. A continuación, da las normas para abordar cinco tipos de combinaciones de fracciones,	+	*'''Fracciones:''' Al comienzo del capítulo doce de su ''Brahmasphutasiddhanta'', titulado ''Cálculo'', Brahmagupta detalla operaciones con fracciones. Da por supuesto que el lector conoce las operaciones aritméticas básicas, como tomar la raíz cuadrada, aunque si explica cómo hallar el cubo y la raíz cúbica de un número entero y, posteriormente, da normas que facilitan el cálculo de cuadrados y raíces cuadradas. A continuación, da las normas para abordar cinco tipos de combinaciones de fracciones,
-	*<math>\cfrac{a}{c} + \cfrac{b}{c}</math>	+	<center><math>\cfrac{a}{c} + \cfrac{b}{c}</math>;{{b}} <math>\cfrac{a}{c} \cdot \cfrac{b}{d}</math>;{{b}} <math>\cfrac{a}{1} + \cfrac{b}{d}</math>;{{b}} <math>\cfrac{a}{c} + \cfrac{b}{d} \cdot \cfrac{a}{c} = \cfrac{a(d+b)}{cd}</math>;{{b}} <math>\cfrac{a}{c} - \cfrac{b}{d} \cdot \cfrac{a}{c} = \cfrac{a(d-b)}{cd}</math></center>
-	*<math>\cfrac{a}{c} \cdot \cfrac{b}{d}</math>	+
-	*<math>\cfrac{a}{1} + \cfrac{b}{d}</math>	+
-	*<math>\cfrac{a}{c} + \cfrac{b}{d} \cdot \cfrac{a}{c} = \cfrac{a(d+b)}{cd}</math>	+
-	*<math>\cfrac{a}{c} - \cfrac{b}{d} \cdot \cfrac{a}{c} = \cfrac{a(d-b)}{cd}</math>.	+
-	====Series====	+	*'''Series:'''
-	Brahmagupta then goes on to give the sum of the squares and cubes of the first ''n'' integers.	+	Brahmagupta continua dando la suma de los cuadrados y los cubos de los primeros "n" enteros. Traduciendo algebraicamente sus palabras sería:
-	<blockquote>12.20. The sum of the squares is that [sum] multiplied by twice the [number of] step[s] increased by one [and] divided by three. The sum of the cubes is the square of that [sum] Piles of these with identical balls [can also be computed].<ref name="Plofker Brahmagupta quote Chapter 12">{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 421–427 | title = }}</ref></blockquote>	+
-	It is important to note here Brahmagupta found the result in terms of the ''sum'' of the first ''n'' integers, rather than in terms of ''n'' as is the modern practice.<ref name="Plofker 423">{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 423 | title = | quote = Here the sums of the squares and cubes of the first ''n'' integers are defined in terms of the sum of the ''n'' integers itself;}}</ref>	+
-	He gives the sum of the squares of the first n natural numbers as n(n+1)(2n+1)/6 and the sum of the cubes of the first n natural numbers as (n(n+1)/2)².	+	#Suma de los cuadrados de los n primeros números naturales: <math>n\cdot(n+1)\cdot \frac{2n+1}{6}</math>
		+	#Suma de los cubos de los n primeros números naturales:<math>\left( \cfrac {n\cdot(n+1)}{2} \right)^2</math>.
-	==== Zero ====	+	*'''El cero y los números negativos:'''
-	Brahmagupta made use of an important concept in mathematics, the [[0 (number)|number zero]]. The ''Brahmasphutasiddhanta'' is the earliest known text to treat zero as a number in its own right, rather than as simply a placeholder digit in representing another number as was done by the [[Babylonians]] or as a symbol for a lack of quantity as was done by [[Ptolemy]] and the [[Ancient Rome|Romans]]. In chapter eighteen of his ''Brahmasphutasiddhanta'', Brahmagupta describes operations on negative numbers. He first describes addition and subtraction,	+	Brahmagupta hace uso del '''número cero''' en su ''Brahmasphutasiddhanta'', siendo este el primer texto conocido en el cual se trata al cero con entidad propia, más que como un simple dígito usado para representar otros números, como hacían los babilonios, o como símbolo para indicar la carencia de una cantidad, como hacía Ptolomeo y los romanos. En el capítulo octavo de ''Brahmasphutasiddhanta'', Brahmagupta describes operaciones con '''númeroas negativos'''. Primero describe la suma y la resta, luego prosigue con la multiplicación dando una correcta regla de los signos, pero al dar la división lo estropea permitiendo la división por cero. Brahmagupta, por ejemplo, dice que: <math>\frac{0}{0} = 0</math>
-	<blockquote>18.30. [The sum] of two positives is positives, of two negatives negative; of a positive and a negative [the sum] is their difference; if they are equal it is zero. The sum of a negative and zero is negative, [that] of a positive and zero positive, [and that] of two zeros zero.<BR>	+
-	[...]<BR>	+
-	18.32. A negative minus zero is negative, a positive [minus zero] positive; zero [minus zero] is zero. When a positive is to be subtracted from a negative or a negative from a positive, then it is to be added.<ref name="Plofker Chapter 18 Brahmasphutasiddhanta">{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 428–434 | title = }}</ref></blockquote>	+
-	He goes on to describe multiplication,	+	===Análisis diofántico===
-	<blockquote>18.33. The product of a negative and a positive is negative, of two negatives positive, and of positives positive; the product of zero and a negative, of zero and a positive, or of two zeros is zero.<ref name="Plofker Chapter 18 Brahmasphutasiddhanta"/></blockquote>	+	*'''Ternas pitagóricas:''' En el capítulo doce de ''Brahmasphutasiddhanta'', Brahmagupta halla ternas pitagóricas. Expresandolo en términos algebraicos:
		+	Para una longitud dada <math>m\;</math> y un multiplicador arbitrario <math>x\;</math>, sean <math>a=mx\;</math> y <math>b=m+ \cfrac{mx}{(x + 2)}</math>. Entonces <math>m\;</math>, <math>a\;</math>, y <math>b\;</math> forman una terna pitagórica.
-	But then he spoils the matter some what when he describes division,	+	*'''Ecuación de Pell:''' Brahmagupta da una relación de recurrencia para generar soluciones de ciertos tipos de ecuaciones diofánticas de segundo grado, tales como <math>Nx^2 + 1 = y^2</math> (llamada ecuación de Pell), usando el algoritmo de [[Euclides]]. El algoritmo de Euclides le era conocido con el nombre de "pulverizador" ya que simplificaba los números.
-	<blockquote>18.34. A positive divided by a positive or a negative divided by a negative is positive; a zero divided by a zero is zero; a positive divided by a negative is negative; a negative divided by a positive is [also] negative.<BR>	+
-	18.35. A negative or a positive divided by zero has that [zero] as its divisor, or zero divided by a negative or a positive [has that negative or positive as its divisor]. The square of a negative or of a positive is positive; [the square] of zero is zero. That of which [the square] is the square is [its] square-root.<ref name="Plofker Chapter 18 Brahmasphutasiddhanta"/></blockquote>	+
-	Here Brahmagupta states that <math>\tfrac{0}{0} = 0</math> and as for the question of <math>\tfrac{a}{0}</math> where <math>a \neq 0</math> he did not commit himself.<ref name="Boyer Brahmagupta p220">{{cite book|last=Boyer|authorlink=Carl Benjamin Boyer|title=|year=1991|chapter=China and India|pages=220|quote=However, here again Brahmagupta spoiled matters somewhat by asserting that <math>0 \div 0 = 0</math>, and on the touchy matter of <math>a \div 0</math>, he did not commit himself:}}</ref> His rules for [[arithmetic]] on [[negative number]]s and zero are quite close to the modern understanding, except that in modern mathematics division by zero is left [[defined and undefined|undefined]].	+	La clave para su solución era la identidad:
-	=== Diophantine analysis ===	+	<center><math>(x^2_1 - Ny^2_1)(x^2_2 - Ny^2_2) = (x_1 x_2 + Ny_1 y_2)^2 - N(x_1 y_2 + x_2 y_1)^2</math></center>
-	==== Pythagorean triples ====	+
-	In chapter twelve of his ''Brahmasphutasiddhanta'', Brahmagupta finds Pythagorean triples,	+
-	<blockquote>12.39. The height of a mountain multiplied by a given multiplier is the distance to a city; it is not erased. When it is divided by the multiplier increased by two it is the leap of one of the two who make the same journey.<ref name="Plofker Brahmagupta quote Chapter 12"/></blockquote>	+
-	or in other words, for a given length ''m'' and an arbitrary multiplier ''x'', let a = ''mx'' and ''b = m + mx/(x + 2)''. Then ''m'', ''a'', and ''b'' form a Pythagorean triple.<ref name="Plofker Brahmagupta quote Chapter 12"/>	+
-	==== Pell's equation ====	+	que es una generalización de una identidad descubierta por [[Diofanto]],
-	Brahmagupta went on to give a recurrence relation for generating solutions to certain instances of Diophantine equations of the second degree such as <math>Nx^2 + 1 = y^2</math> (called [[Pell's equation]]) by using the [[Euclidean algorithm]]. The Euclidean algorithm was known to him as the "pulverizer" since it breaks numbers down into ever smaller pieces.<ref>{{cite book | first = John | last = Stillwell | year = 2004 | pages = 44–46 | title = | quote = In the seventh century CE the Indian mathematician Brahmagupta gave a recurrence relation for generating solutions of <math>x^2 - Dy^2 = 1</math>, as we shall see in Chapter 5. The Indians called the Euclidean algorithm the "pulverizer" because it breaks numbers down to smaller and smaller pieces. To obtain a recurrence one has to know that a rectangle proportional to the original eventually recurs, a fact that was rigorously proved only in 1768 by Lagrange.}}</ref>	+
-	<blockquote>The nature of squares:<BR>18.64. [Put down] twice the square-root of a given square by a multiplier and increased or diminished by an arbitrary [number]. The product product of the first [pair], multiplied by the multiplier, with the product of the last [pair], is the last computed.<BR>18.65. The sum of the thunderbolt products is the first. The additive is equal to the product of the additives. The two square-roots, divided by the additive or the subtractive, are the additive ''rupas''.<ref name="Plofker Chapter 18 Brahmasphutasiddhanta"/></blockquote>	+	<center><math>(x^2_1 - y^2_1)(x^2_2 - y^2_2) = (x_1 x_2 + y_1 y_2)^2 - (x_1 y_2 + x_2 y_1)^2.</math></center>
-	The key to his solution was the identity,<ref name="Stillwell p. 72-74"/>	+	Usando esta identidad y el hecho de que si<math>(x_1,</math> <math>y_1)\;</math> and <math>(x_2,\;</math> <math>y_2)\;</math> son soluciones de las ecuaciones <math>x^2 - Ny^2 = k_1\;</math> y <math>x^2 - Ny^2 = k_2\;</math>, respectivamente, entonces <math>(x_1 x_2 + N y_1 y_2,\;</math> <math>x_1 y_2 + x_2 y_1)\;</math> es una solución de <math>x^2 - Ny^2 = k_1 k_2\;</math>, él supo encontrar soluciones enteras de la ecuación de Pell equation mediante una serie de ecuaciones de la forma <math>x^2 - Ny^2 = k_i\;</math>. Por desgracia, Brahmagupta no fue capaz de aplicar su solución de forma uniforme para todos los posibles valores de ''N'', sino que sólo pudo demostrar que si <math>x^2 - Ny^2 = k\;</math> tiene una solución entera para <math>k = \pm 1, \pm 2, \pm 4</math>, entonces <math>x^2 - Ny^2 = 1\;</math> tiene una solución. la solución de la ecuación general de Pell tendría que esperar a [[Bhaskara II]] (c. 1150)
-	:<math>(x^2_1 - Ny^2_1)(x^2_2 - Ny^2_2) = (x_1 x_2 + Ny_1 y_2)^2 - N(x_1 y_2 + x_2 y_1)^2</math>	+	===Geometría ===
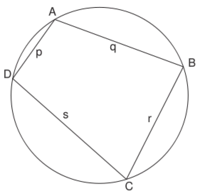
		+	*'''Fórmula de Brahmagupta:''' El resultado en geometría más famoso de Brahmagupta es su fórmula para los cuadriláteros cíclicos (aquellos inscritos en una circunferencia).
		+	[[Image:Cuadrilatero_ciclico.png|200px|thumb|right|Cuadrilátero cíclico]]
		+	Dadas las longitudes de los lados de un cuadrilátero cíclico cualquiera, Brahmagupta dió una fórmula aproximada y otra exacta para el área de dicha figura. la traducción algebraica diría: Dadas las longitudes <math>p\;</math>, <math>q\;</math>, <math>r\;</math> y <math>s\;</math> de un cuadrilátero cíclico,
-	which is a generalization of an identity that was discovered by [[Diophantus]],	+	*Area aproximada: <math>A=(\cfrac{p + r}{2}) (\cfrac{q + s}{2})</math>
		+	*Area exacta:<math>\sqrt{(t - p)(t - q)(t - r)(t - s)}</math>, donde <math>t = \cfrac{p + q + r + s}{2}</math>.
-	:<math>(x^2_1 - y^2_1)(x^2_2 - y^2_2) = (x_1 x_2 + y_1 y_2)^2 - (x_1 y_2 + x_2 y_1)^2.</math>	+	Aunque Brahmagupta no enuncia explícitamente que se trate de cuadriláteros cíclicos, parece deducirse de sus reglas que ese es el caso.
-	Using his identity and the fact that if <math>(x_1,</math> <math>y_1)</math> and <math>(x_2,</math> <math>y_2)</math> are solutions to the equations <math>x^2 - Ny^2 = k_1</math> and <math>x^2 - Ny^2 = k_2</math>, respectively, then <math>(x_1 x_2 + N y_1 y_2,</math> <math>x_1 y_2 + x_2 y_1)</math> is a solution to <math>x^2 - Ny^2 = k_1 k_2</math>, he was able to find integral solutions to the Pell's equation through a series of equations of the form <math>x^2 - Ny^2 = k_i</math>. Unfortunately, Brahmagupta was not able to apply his solution uniformly for all possible values of ''N'', rather he was only able to show that if <math>x^2 - Ny^2 = k</math> has an integral solution for k = <math>\pm 1, \pm 2, \pm 4</math> then <math>x^2 - Ny^2 = 1</math> has a solution. The solution of the general Pell's equation would have to wait for [[Bhaskara II]] in c. 1150 CE.<ref name="Stillwell p. 72-74">{{cite book | first = John | last = Stillwell | year = 2004 | pages = 72–74 | title = }}</ref>	+	La '''fórmula de [[Heron]]''' se obtiene como caso particular de la de Brahmagupta, haciendo uno de los lados igual a cero.
-	===Geometry ===	+	*'''Triángulos:''' Uno de los teoremas en la obra de Brahmagupta dice que las medidas de los dos segmentos en que la altura de un triángulo divide a la base son:
-	==== Brahmagupta's formula ====	+	<center><math>b \pm \cfrac{c^2 - a^2}{b}</math></center>
-	[[Image:Brahmaguptas formula.svg|200px|thumb|right|Diagram for reference]]	+
-	{{main|Brahmagupta's formula}}	+
-	Brahmagupta's most famous result in geometry is his [[Brahmagupta's formula|formula]] for [[cyclic quadrilaterals]]. Given the lengths of the sides of any cyclic quadrilateral, Brahmagupta gave an approximate and an exact formula for the figure's area,	+	Además da un teorema sobre triángulos racionales (cuyos lados son números racionales):
-	<blockquote>12.21. The approximate area is the product of the halves of the sums of the sides and opposite sides of a triangle and a quadrilateral. The accurate [area] is the square root from the product of the halves of the sums of the sides diminished by [each] side of the quadrilateral.<ref name="Plofker Brahmagupta quote Chapter 12"/></blockquote>	+	Un triángulo con lados racionales <math>a\;</math>, <math>b\;</math> y <math>c\;</math> y área racional es de la forma:
-	So given the lengths ''p'', ''q'', ''r'' and ''s'' of a cyclic quadrilateral, the approximate area is <math>(\tfrac{p + r}{2}) (\tfrac{q + s}{2})</math> while, letting <math>t = \tfrac{p + q + r + s}{2}</math>, the exact area is	+
-	: <math>\sqrt{(t - p)(t - q)(t - r)(t - s)}.</math>	+	<center><math>a = \frac{1}{2}\left(\frac{u^2}{v}+v\right), \ \ b = \frac{1}{2}\left(\frac{u^2}{w}+w\right), \ \ c = \frac{1}{2}\left(\frac{u^2}{v} - v + \frac{u^2}{w} - w\right) </math></center>
-	Although Brahmagupta does not explicitly state that these quadrilaterals are cyclic, it is apparent from his rules that this is the case.<ref>{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 424 | title = | quote = Brahmagupta does not explicitly state that he is discussing only figures inscribed in circles, but it is implied by these rules for computing their circumradius.}}</ref> [[Heron's formula]] is a special case of this formula and it can be derived by setting one of the sides equal to zero.	+	para algunos racionales <math>u\;</math>, <math>v\;</math>, y <math>w\;</math>.
-	==== Triangles ====	+	*Teorema de Brahmagupta:
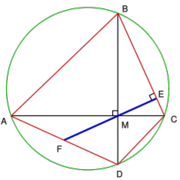
-	Brahmagupta dedicated a substantial portion of his work to geometry. One theorem states that the two lengths of a triangle's base when divided by its altitude then follows,	+	[[Image:Brahmagupta_teorema.png|thumb|right|El teorema de Brahmagupta dice que ''AF'' = ''FD''.]]
-	<blockquote>12.22. The base decreased and increased by the difference between the squares of the sides divided by the base; when divided by two they are the true segments. The perpendicular [altitude] is the square-root from the square of a side diminished by the square of its segment.<ref name="Plofker Brahmagupta quote Chapter 12"/></blockquote>	+	Brahmagupta continua diciendo que, en un cuadrilátero cíclico "no desigual" (trapezoide equilatero), la longitud de las diagonales es:
-	Thus the lengths of the two segments are <math>b \pm (c^2 - a^2)/b</math>.	+	<center><math>\sqrt{pr + qs}</math></center>
		+	Sigue dando las fórmulas de las longitudes y áreas de figuras geométricas como la medida del radio de la circunferencia circunscrita al trapezoide isósceles y del cuadrilátero escaleno, y las medidas de las diagonales de un cuadrilátero cíclico escaleno. Esto lleva al famoso teorema de Brahmagupta. (ver dibujo adjunto)
-	He further gives a theorem on [[rational triangles]]. A triangle with rational sides ''a'', ''b'', ''c'' and rational area is of the form:	+	*'''Pi:''' En el verso 40, da valores del número Pi: 3 como valor práctico de Pi y <math>\sqrt{10}</math> como valor más preciso.
-	:<math>a = \frac{1}{2}\left(\frac{u^2}{v}+v\right), \ \ b = \frac{1}{2}\left(\frac{u^2}{w}+w\right), \ \ c = \frac{1}{2}\left(\frac{u^2}{v} - v + \frac{u^2}{w} - w\right) </math>	+	*'''Medidas y construcciones:'''
		+	En algunos de los versos anteriores al 40, Brahmagupta da la construcción de varias figuras con lados arbitrarios. El manipuló esencialmente triángulos rectángulos para obtener trángulos isósceles, triángulos escalenos, rectángulos, trapezoides isósceles, trapezoides isósceles con tres lados iguales, y cuadriláteros cíclicos escalenos.
-	for some rational numbers ''u'', ''v'', and ''w''.<ref>{{Harv|Stillwell|2004|p=77}}</ref>	+	Tras dar el valor de Pi, trata aspectos de la geometría planas y de sólidos, como encontrar sus volúmenes y superficies. Halla el volumen de prismas rectos, pirámides, y troncos de pirámides de base cuadrada.
-	==== Brahmagupta's theorem ====	+	===Trigonometría===
-	{{main|Brahmagupta theorem}}	+	En el capítulo 2 de ''Brahmasphutasiddhanta'', titulado ''Longitudes Planetarias Verdaderas'', Brahmagupta presenta una tabla de senos, usando nombres de objetos para representar los números, algo que era común en los tratatados en sanscrito. Así, por ejemplo, "Osa mayor" representa el 7 (por las 7 estrellas de dicha constelación), "gemelos" al 2, "Vedas" el 4 (por los 4 Vedas), Progenitores el 14, etc. esta información, traducida en números, da la lista de senos: 214 (gemelos, Progenitores), 427 (Osa Mayor, gemelos, Vedas), 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, y 3270, siendo el radio 3270.
-	[[Image:Brahmaguptra's theorem.svg|thumb|right|Brahmagupta's theorem states that ''AF'' = ''FD''.]]	+
-	Brahmagupta continues,	+	==Astronomía==
-	<blockquote>12.23. The square-root of the sum of the two products of the sides and opposite sides of a non-unequal quadrilateral is the diagonal. The square of the diagonal is diminished by the square of half the sum of the base and the top; the square-root is the perpendicular [altitudes].<ref name="Plofker Brahmagupta quote Chapter 12"/></blockquote>	+	Fue a traves de el ''Brahmasphutasiddhanta'' como los árabes aprendieron la astronomía hindú. El famoso califa abasida Al-Mansur (712–775), fundó Baghdad, situada a orillas del Tigris, e la hizo centro de aprendizaje. El califa invitó a un estudiante de Ujjain llamado Kankah en 770 a.C. Kankah usó el ''Brahmasphutasiddhanta'' para explicar el sistema hindú de astronomía aritmética. Muhammad al-Fazari tradujo el trabajo de Brahmugupta al árabe a demanda del califa.
-	So, in a "non-unequal" cyclic quadrilateral (that is, an isosceles [[trapezoid]]), the length of each diagonal is <math>\sqrt{pr + qs}</math>.	+
-	He continues to give formulas for the lengths and areas of geometric figures, such as the circumradius of an isosceles trapezoid and a scalene quadrilateral, and the lengths of diagonals in a scalene cyclic quadrilateral. This leads up to [[Brahmagupta's theorem|Brahmagupta's famous theorem]],	+	En el capítulo siete de ''Brahmasphutasiddhanta'', titulado ''Creciente Lunar'', Brahmagupta refuta la idea de que la Luna se encuentra más alejada que el Sol de la Tierra, idea que se mantuvo en las escrituras. El hace ésto explicando la iluminación de la Luna por el Sol. También explicó que, como la Luna está más cerca de la Tierra que el Sol, la cantidad de parte iluminada de la Luna depende de la posición relativa del Sol y la Luna, y esto puede calcularse a partir del ángulo que forman los dos cuerpos.
-	<blockquote>12.30-31. Imaging two triangles within [a cyclic quadrilateral] with unequal sides, the two diagonals are the two bases. Their two segments are separately the upper and lower segments [formed] at the intersection of the diagonals. The two [lower segments] of the two diagonals are two sides in a triangle; the base [of the quadrilateral is the base of the triangle]. Its perpendicular is the lower portion of the [central] perpendicular; the upper portion of the [central] perpendicular is half of the sum of the [sides] perpendiculars diminished by the lower [portion of the central perpendicular].<ref name="Plofker Brahmagupta quote Chapter 12"/></blockquote>	+
-	==== Pi ====	+	Algunas de las aportaciones de importancia hechas por Brahmagupta a la astronomía son: métodos para calcular la posición de cuerpos celestes en el tiempo (efemérides), su aparición y su ocultación, conjunciones, y el cálculo de los eclipses solares y lunares. Brahmagupta criticó el punto de vista puránico de que la Tierra era plana o hueca. Por el contrario, observó que la Tierra y el cielo eran esféricos y que la Tierra se mueve. En el año 1030, el astrónomo musulmán, Abu al-Rayhan al-Biruni, en su ''Ta'rikh al-Hind'', posteriormente traducido al latín como ''Indica'', comentó el trabajo de Brahmaguptas y escribió que los críticos argumentaron:
-	In verse 40, he gives values of [[pi|''&pi;'']],	+
-	<blockquote>12.40. The diameter and the square of the radius [each] multiplied by 3 are [respectively] the practical circumference and the area [of a circle]. The accurate [values] are the square-roots from the squares of those two multiplied by ten.<ref name="Plofker Brahmagupta quote Chapter 12"/></blockquote>	+
-	So Brahmagupta uses 3 as a "practical" value of ''&pi;'', and <math>\sqrt{10}</math> as an "accurate" value of ''&pi;''.	+
-	==== Measurements and constructions ====	+	"Si eso es así, las piedras y los árboles se caerían de la Tierra."
-	In some of the verses before verse 40, Brahmagupta gives constructions of various figures with arbitrary sides. He essentially manipulated right triangles to produce isosceles triangles, scalene triangles, rectangles, isosceles trapezoids, isosceles trapezoids with three equal sides, and a scalene cyclic quadrilateral.	+
-	After giving the value of pi, he deals with the geometry of plane figures and solids, such as finding volumes and surface areas (or empty spaces dug out of solids). He finds the volume of rectangular prisms, pyramids, and the frustrum of a square pyramid. He further finds the average depth of a series of pits. For the volume of a [[frustum]] of a pyramid, he gives the "pragmatic" value as the depth times the square of the mean of the edges of the top and bottom faces, and he gives the "superficial" volume as the depth times their mean area.<ref>"{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 427 | title = | quote = After the geometry of plane figures, Brahmagupta discusses the computation of volumes and surface areas of solids (or empty spaces dug out of solids). His straight-forward rules for the volumes of a rectangular prism and pyramid are followed by a more ambiguous one, which may refer to finding the average depth of a sequence of puts with different depths. The next formula apparently deals with the volume of a frustum of a square pyramid, where the "pragmatic" volume is the depth times the square of the mean of the edges of the top and bottom faces, while the "superficial" volume is the depth times their mean area.}}</ref>	+	De acuerdo con al-Biruni, Brahmagupta respondió a estas críticas con el siguiente argumento sobre gravitación:
-		+	... Todas las cosas pesadas son atraidas hacia el centro de la Tierra... La Tierra es igual por todos lados; todo el mundo sobre la Tierra permanece derecho, y todas las cosas pesadas caen a al Tierra por una ley de la naturaleza, porque está en la naturaleza de la Tierra atraer y mantener las cosas, como está en la naturaleza del agua fluir, en la del fuego quemar, y en la del viento mantenerse en movimientootion..."
-	=== Trigonometry ===	+
-	{{Mergefrom|Brahmagupta interpolation formula|Talk:Brahmagupta interpolation formula#Proposal to merge into Brahmagupta article|subst:DATE|date=September 2008}}	+
-	In Chapter 2 of his ''Brahmasphutasiddhanta'', entitled ''Planetary True Longitudes'', Brahmagupta presents a sine table:	+
-		+
-	<blockquote>2.2-5. The sines: The Progenitors, twins; Ursa Major, twins, the Vedas; the gods, fires, six; flavors, dice, the gods; the moon, five, the sky, the moonl the moon, arrows, suns [...]<ref>{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 419 | title =}}</ref></blockquote>	+
-		+
-	Here Brahmagupta uses names of objects to represent the digits of place-value numerals, as was common with numerical data in Sanskrit treatises. Progenitors represents the 14 Progenitors ("Manu") in Indian cosmology or 14, "twins" means 2, "Ursa Major" represents the seven stars of Ursa Major or 7, "Vedas" refers to the 4 Vedas or 4, dice represents the number of sides of the tradition die or 6, and so on. This information can be translated into the list of sines, 214, 427, 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, and 3270, with the radius being 3270.<ref name="Plofker 419&ndash;420"/>	+
-		+
-	In his ''Paitamahasiddhanta'', Brahmagupta uses the initial sine value of 225 with a radius of approximately 3438, although the rest of the sine table is lost. The value of 3438 for the radius is a traditional value that was also used by Aryabhata, although it is not known why Brahmagupta used 3270 instead of the 3438 in his ''Brahmasphutasiddhanta''.<ref name="Plofker 419&ndash;420">{{cite book | first = Kim | last = Plofker | year = 2007 | pages = 419&ndash;420 | title = | quote = Brahmagupta's sine table, like much other numerical data in Sanskrit treatises, is encoded mostly in concrete-number notation that uses names of objects to represent the digits of place-value numerals, starting with the least significant. [...]<BR>There are fourteen Progenitors ("Manu") in Indian cosmology; "twins" of course stands for 2; the seven stars of Ursa Major (the "Sages") for 7, the four Vedas, and the four sides of the traditional dice used in gambling, for 6, and so on. Thus Brahmagupta enumerates his first six sine-values as 214, 427, 638, 846, 1051, 1251. (His remaining eighteen sines are 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, 3270. The ''Paitamahasiddhanta'', however, specifies an initial sine-value of 225 (although the rest of its sine-table is lost), implying a trigonometric radius of ''R'' = 3438 aprox= C(')/2π: a tradition followed, as we have seen, by Aryabhata. Nobody knows why Brahmagupta chose instead to normalize these values to R = 3270.}}</ref>	+
	[[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]]		[[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]]

---

Revisión actual

Brahmagupta (598–668), matemático y astrónomo indú.

Tabla de contenidos 1 Vida y obra 2 Matemáticas 2.1 Algebra 2.2 Aritmética 2.3 Análisis diofántico 2.4 Geometría 2.5 Trigonometría 3 Astronomía

Vida y obra

Brahmagupta nació en el año 598 en Bhinmal, ciudad en el estado de Rajasthan, al noroeste de la India. Probablemente vivió la mayor parte de su vida en Bhillamala (moderna Bhinmal, en Rajasthan) en el imperio de Harsha, durante el reinado del Rey Vyaghramukha. Como resultado de ello, Brahmagupta es a menudo citado como Bhillamalacarya que quiere decir, el maestro de Bhillamala Bhinmal.

Fue el jefe del observatorio astronómico en Ujjain, y durante su mandato allí escribió cuatro textos sobre las matemáticas y la astronomía: Cadamekela en el 624, Brahmasphutasiddhanta en 628, Khandakhadyaka en 665, y Durkeamynarda en 672. El Brahmasphutasiddhanta (Tratado corregido de Brahma) es posiblemente su obra más famosa. El historiador Al-Biruni (c. 1050) en su libro Tariq al-Hind, afirma que el califa Abbasid al-Ma'mun, que tenía una embajada en la India, llevó de3 allí un libro a Bagdad que fue traducido al árabe como Sindhind. Se presume que Sindhind no es otro que Brahmagupta-Brahmasphuta Siddhanta.

Aunque Brahmagupta estaba familiarizado con las obras de los astrónomos siguiendo la tradición de Aryabhatiya, no se sabe si está familiarizado con la labor de Bhaskara I, un contemporáneo. Brahmagupta tenía una cantidad de críticas dirigidas hacia la labor de los astrónomos rivales, y en su Brahmasphutasiddhanta se encuentra uno de los primeros cismas de fe entre matemáticos indios. La división fue principalmente sobre la aplicación de las matemáticas al mundo físico, más que sobre las matemáticas en si mismas. En el caso de Brahmagupta, los desacuerdos se debieron en gran parte de la elección de las teorías y parámetros astronómicos. A lo largo de los primeros diez capítulos astronómicos aparecen críticas a las teorías rivales, y el undécimo capítulo está completamente dedicado a la crítica de estas teorías, aunque las críticas no aparecen en el duodécimo y décimo octavo capítulos.

Matemáticas

La obra más famosa de Brahmagupta es su Brahmasphutasiddhanta. Compuesta en verso elíptico, practica común en las matemáticas indueshematics]], la obra tiene, en consecuencia, un cierto halo poético. Como en ella no se dan demostraciones, no se sabe como Brahmagupta obtenía los resultados matemáticos.

Algebra

Brahmagupta da la solución de la ecuación lineal general en el capítulo dieciocho de Brahmasphutasiddhanta, que aunque expresada en el libro en palabras, viene a ser equivalente a la siuiente expresión algebraica:

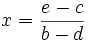
Además, dio dos soluciones equivalentes para la ecuación general de segundo grado, que vienen a ser equivalentes, respectivamente, a las siguientes expresiones algebraicas:

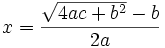
y

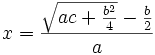
El contina resolviendo sistemas de ecuaciones indeterminados, enunciando que la variable elegida debe primero aislarse, y que luego la ecuación debe dividirse por el coeficiente de la variable elegida.

Al igual que el álgebra de Diofanto, el álgebra de Brahmagupta es sincopada. La suma la indicaba colocando los números uno al lado del otro, la resta colocando un punto sobre el sustraendo, la división colocando el divisor debajo del dividendo, similar a nuestra notación, pero sin la barra. La multiplicación, las raices y las incógnitas las representaba mediante abrebiaturas de términos apropiados. Fue el primero en dar una solución general a la ecuación lineal de Diofanto ax + by = c, donde a, b, y c son enteros. También es muy posible que diese todas las soluciones de dicha ecuación, mientras que Diofanto se sintió satisfecho con dar una sola solución de una ecuación indeterminada. En la medida en que Brahmagupta utilizó algunos ejemplos iguales a los de Diofanto, vemos la posibilidad de que ambos hubiesen usado las mismas fuentes, posiblemente babilónicas. No se sabe hasta que punto el uso de la notación sincopada en el álgebra de Brahmagupta es debido a los griegos o si tanto griegos como hindues derivan su uso de una fuente común usase notación sincopada, no se conoce y es posible que tanto el griego y el indio síncopa pueden derivarse de una fuente común, las matemáticas babilónicas.

Aritmética

• Fracciones: Al comienzo del capítulo doce de su Brahmasphutasiddhanta, titulado Cálculo, Brahmagupta detalla operaciones con fracciones. Da por supuesto que el lector conoce las operaciones aritméticas básicas, como tomar la raíz cuadrada, aunque si explica cómo hallar el cubo y la raíz cúbica de un número entero y, posteriormente, da normas que facilitan el cálculo de cuadrados y raíces cuadradas. A continuación, da las normas para abordar cinco tipos de combinaciones de fracciones,

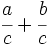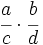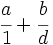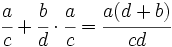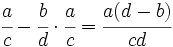
• Series:

Brahmagupta continua dando la suma de los cuadrados y los cubos de los primeros "n" enteros. Traduciendo algebraicamente sus palabras sería:

1. Suma de los cuadrados de los n primeros números naturales:
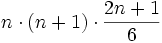
2. Suma de los cubos de los n primeros números naturales:.

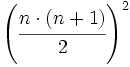• El cero y los números negativos:

Brahmagupta hace uso del número cero en su Brahmasphutasiddhanta, siendo este el primer texto conocido en el cual se trata al cero con entidad propia, más que como un simple dígito usado para representar otros números, como hacían los babilonios, o como símbolo para indicar la carencia de una cantidad, como hacía Ptolomeo y los romanos. En el capítulo octavo de Brahmasphutasiddhanta, Brahmagupta describes operaciones con númeroas negativos. Primero describe la suma y la resta, luego prosigue con la multiplicación dando una correcta regla de los signos, pero al dar la división lo estropea permitiendo la división por cero. Brahmagupta, por ejemplo, dice que: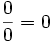

Análisis diofántico

• Ternas pitagóricas: En el capítulo doce de Brahmasphutasiddhanta, Brahmagupta halla ternas pitagóricas. Expresandolo en términos algebraicos:

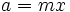Para una longitud dada y un multiplicador arbitrario , sean y 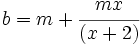. Entonces , , y forman una terna pitagórica.

• Ecuación de Pell: Brahmagupta da una relación de recurrencia para generar soluciones de ciertos tipos de ecuaciones diofánticas de segundo grado, tales como Nx² + 1 = y² (llamada ecuación de Pell), usando el algoritmo de Euclides. El algoritmo de Euclides le era conocido con el nombre de "pulverizador" ya que simplificaba los números.

La clave para su solución era la identidad:

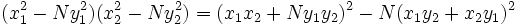
que es una generalización de una identidad descubierta por Diofanto,

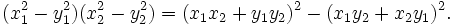
Usando esta identidad y el hecho de que si(x₁, and 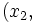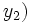son soluciones de las ecuaciones 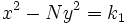y 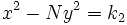, respectivamente, entonces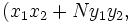 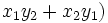es una solución de 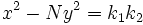, él supo encontrar soluciones enteras de la ecuación de Pell equation mediante una serie de ecuaciones de la forma 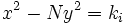. Por desgracia, Brahmagupta no fue capaz de aplicar su solución de forma uniforme para todos los posibles valores de N, sino que sólo pudo demostrar que si 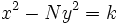tiene una solución entera para 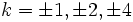, entonces 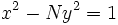tiene una solución. la solución de la ecuación general de Pell tendría que esperar a Bhaskara II (c. 1150)

Geometría

• Fórmula de Brahmagupta: El resultado en geometría más famoso de Brahmagupta es su fórmula para los cuadriláteros cíclicos (aquellos inscritos en una circunferencia).

Dadas las longitudes de los lados de un cuadrilátero cíclico cualquiera, Brahmagupta dió una fórmula aproximada y otra exacta para el área de dicha figura. la traducción algebraica diría: Dadas las longitudes 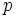, , 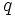y 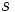de un cuadrilátero cíclico,

• Area aproximada:
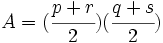
• Area exacta: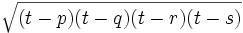, donde .

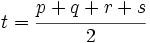Aunque Brahmagupta no enuncia explícitamente que se trate de cuadriláteros cíclicos, parece deducirse de sus reglas que ese es el caso.

La fórmula de Heron se obtiene como caso particular de la de Brahmagupta, haciendo uno de los lados igual a cero.

• Triángulos: Uno de los teoremas en la obra de Brahmagupta dice que las medidas de los dos segmentos en que la altura de un triángulo divide a la base son:

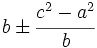
Además da un teorema sobre triángulos racionales (cuyos lados son números racionales): Un triángulo con lados racionales , y y área racional es de la forma:

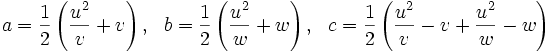
para algunos racionales 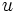, , 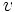y .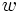

• Teorema de Brahmagupta:

Brahmagupta continua diciendo que, en un cuadrilátero cíclico "no desigual" (trapezoide equilatero), la longitud de las diagonales es:

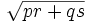
Sigue dando las fórmulas de las longitudes y áreas de figuras geométricas como la medida del radio de la circunferencia circunscrita al trapezoide isósceles y del cuadrilátero escaleno, y las medidas de las diagonales de un cuadrilátero cíclico escaleno. Esto lleva al famoso teorema de Brahmagupta. (ver dibujo adjunto)

• Pi: En el verso 40, da valores del número Pi: 3 como valor práctico de Pi y 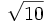como valor más preciso.

• Medidas y construcciones:

En algunos de los versos anteriores al 40, Brahmagupta da la construcción de varias figuras con lados arbitrarios. El manipuló esencialmente triángulos rectángulos para obtener trángulos isósceles, triángulos escalenos, rectángulos, trapezoides isósceles, trapezoides isósceles con tres lados iguales, y cuadriláteros cíclicos escalenos.

Tras dar el valor de Pi, trata aspectos de la geometría planas y de sólidos, como encontrar sus volúmenes y superficies. Halla el volumen de prismas rectos, pirámides, y troncos de pirámides de base cuadrada.

Trigonometría

En el capítulo 2 de Brahmasphutasiddhanta, titulado Longitudes Planetarias Verdaderas, Brahmagupta presenta una tabla de senos, usando nombres de objetos para representar los números, algo que era común en los tratatados en sanscrito. Así, por ejemplo, "Osa mayor" representa el 7 (por las 7 estrellas de dicha constelación), "gemelos" al 2, "Vedas" el 4 (por los 4 Vedas), Progenitores el 14, etc. esta información, traducida en números, da la lista de senos: 214 (gemelos, Progenitores), 427 (Osa Mayor, gemelos, Vedas), 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, y 3270, siendo el radio 3270.

Astronomía

Fue a traves de el Brahmasphutasiddhanta como los árabes aprendieron la astronomía hindú. El famoso califa abasida Al-Mansur (712–775), fundó Baghdad, situada a orillas del Tigris, e la hizo centro de aprendizaje. El califa invitó a un estudiante de Ujjain llamado Kankah en 770 a.C. Kankah usó el Brahmasphutasiddhanta para explicar el sistema hindú de astronomía aritmética. Muhammad al-Fazari tradujo el trabajo de Brahmugupta al árabe a demanda del califa.

En el capítulo siete de Brahmasphutasiddhanta, titulado Creciente Lunar, Brahmagupta refuta la idea de que la Luna se encuentra más alejada que el Sol de la Tierra, idea que se mantuvo en las escrituras. El hace ésto explicando la iluminación de la Luna por el Sol. También explicó que, como la Luna está más cerca de la Tierra que el Sol, la cantidad de parte iluminada de la Luna depende de la posición relativa del Sol y la Luna, y esto puede calcularse a partir del ángulo que forman los dos cuerpos.

Algunas de las aportaciones de importancia hechas por Brahmagupta a la astronomía son: métodos para calcular la posición de cuerpos celestes en el tiempo (efemérides), su aparición y su ocultación, conjunciones, y el cálculo de los eclipses solares y lunares. Brahmagupta criticó el punto de vista puránico de que la Tierra era plana o hueca. Por el contrario, observó que la Tierra y el cielo eran esféricos y que la Tierra se mueve. En el año 1030, el astrónomo musulmán, Abu al-Rayhan al-Biruni, en su Ta'rikh al-Hind, posteriormente traducido al latín como Indica, comentó el trabajo de Brahmaguptas y escribió que los críticos argumentaron:

"Si eso es así, las piedras y los árboles se caerían de la Tierra."

De acuerdo con al-Biruni, Brahmagupta respondió a estas críticas con el siguiente argumento sobre gravitación: ... Todas las cosas pesadas son atraidas hacia el centro de la Tierra... La Tierra es igual por todos lados; todo el mundo sobre la Tierra permanece derecho, y todas las cosas pesadas caen a al Tierra por una ley de la naturaleza, porque está en la naturaleza de la Tierra atraer y mantener las cosas, como está en la naturaleza del agua fluir, en la del fuego quemar, y en la del viento mantenerse en movimientootion..."