Fermat

De Wikipedia

(Diferencia entre revisiones)

Revisión de 10:27 31 dic 2008

Pierre de Fermat (1601 - 1665), jurista y matemático francés. Fue abogado en el Parlamento de Toulouse, en el sur de Francia, y matemático clave para el desarrollo del cálculo moderno. También hizo notables contribuciones a la geometría analítica.

Fermat es mejor conocido por su Enigma, una abstracción del Teorema de Pitágoras, también conocido como Último Teorema de Fermat, que torturó a los matemáticos durante aproximadamente 350 años, hasta que fue resuelto en 1995. Junto con René Descartes, Fermat fue uno de los líderes matemáticos de la primera mitad del siglo XVII. Independientemente de Descartes, descubrió el principio fundamental de la geometría analítica. A través de su correspondencia con Blaise Pascal, fue co-fundador de la teoría de probabilidades.

Vida

Fermat nació el 17 de agosto de 1601 en Beaumont-de-Lomagne, una ciudad situada a 58 kilómetros al noroeste de Toulouse, Francia.

Poco se conoce de sus primeros años, excepto que estudió derecho, posiblemente en Toulouse y Burdeos.

Extremadamente prolífico, sus deberes profesionales y su particular forma de trabajar (sólo publicó una obra científica en vida) redujeron en gran medida el impacto de su obra. Fermat era un matemático que trabajaba la mayor parte del tiempo en soledad. Su único contacto con el resto de la comunidad matemática fue gracias a Marin Mersenne además de sus correspondencias con Pascal. Los resultados de Fermat fueron conocidos por otros pensadores europeos gracias a Mersenne, que los reenvió e hizo una amplia distribución.

Murió en Castres, Francia, el 12 de enero de 1665.

Curiosidades

La mansión del siglo XV donde nació es en la actualidad un museo.
La escuela más antigua y prestigiosa de Toulouse se llama Pierre de Fermat y en ella se imparten clases de ingeniería y comercio. Está situada entre las diez mejores de Francia para clases preparatorias.
Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre, (12007) Fermat.
También se le ha dado su nombre a un cráter lunar de 39 km de diámetro.
Películas: "La habitación de Fermat"

Obra

Interesado por las matemáticas, en 1629 abordó la tarea de reconstruir algunas de las demostraciones perdidas del matemático griego Apolonio relativas a los lugares geométricos; a tal efecto desarrollaría, contemporánea e independientemente de René Descartes, un método algebraico para tratar cuestiones de geometría por medio de un sistema de coordenadas.

Diseñó un algoritmo de diferenciación mediante el cual pudo determinar los valores máximos y mínimos de una curva polinómica, amén de trazar las correspondientes tangentes, logros todos ellos que abrieron el camino al desarrollo ulterior del cálculo infinitesimal por Newton y Leibniz.

Tras asumir correctamente que cuando la luz se desplaza en un medio más denso su velocidad disminuye, demostró que el camino de un rayo luminoso entre dos puntos es siempre aquel que menos tiempo le cuesta recorrer; de dicho principio, que lleva su nombre, se deducen las leyes de la reflexión y la refracción.

En 1654, y como resultado de una larga correspondencia, desarrolló con su colega Blaise Pascal los principios de la teoría de probabilidad.

Otro campo en el que realizó destacadas aportaciones fue el de la teoría de números, en la que empezó a interesarse tras consultar una edición de la Aritmética de Diofanto. De su trabajo en dicho campo se derivaron importantes resultados relacionados con las propiedades de los números primos, muchas de las cuales quedaron expresadas en forma de simples proposiciones y teoremas. Desarrolló también un ingenioso método de demostración que denominó «del descenso infinito».

Fermat acostumbraba a escribir las soluciones a los problemas en el margen de los libros. Una vez escribió en su ejemplar del texto griego de La Aritmética de Diofanto (editada por Claude Gaspard Bachet de Méziriac en 1621) lo siguiente:

"Cubem autem in duos cubos, aut quadratoquadratorum in duos cuadratosquadratos, et generaliter nullam in infinitum ultra cuadratum potestandem in duos ejusdem nominis dividere: cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exigitas non caparet."

"Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración excelente. El margen es demasiado pequeño para que la demostración quepa en él."

No se sabe si realmente halló la demostración ya que no dejó rastro de ella para que otros matemáticos pudiesen verificarla. Este problema mantuvo en vilo a los matemáticos durante más de tres siglos, hasta que en 1995 Andrew Wiles encontró la demostración. Andrew utilizó para ello herramientas matemáticas que surgieron mucho después de la muerte de Fermat, luego éste debió haber encontrado la solución por otro camino, si es que lo hizo. En cualquier caso, Fermat tenía razón.

Espiral de Fermat

La espiral de Fermat, denominada así en honor de Pierre de Fermat y también conocida como espiral parabólica, es una curva que responde a la siguiente ecuación:

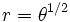
$r = \theta^{1/2}\;$

Es un caso particular de la espiral de Arquímedes.

Números amigos

Los pitagóricos observaron una rara relación entre los números 220 y 284: la suma de los divisores de cada uno de ellos, salvo el propio número, es el otro. Los denominaron números amigos. Durante muchos siglos, la pareja 220 y 284 fueron los únicos amigos conocidos, hasta que en 1636 Fermat descubrió que 17.296 y 18.416 también lo son. En 1638 Descartes, colega y competidor de Fermat, encontró la tercera pareja: 9.363.584 y 9.437.056

Números primos

Un número de Fermat, nombrado en honor a Pierre de Fermat, quien fue el primero que estudió estos números, es un número natural de la forma:

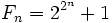
$F_{n} = 2^{2^n} + 1$

donde n es natural. De particular interés son los números primos de Fermat.

Pierre de Fermat conjeturó que todos los números naturales de la forma

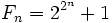
$F_{n} = 2^{2^n} + 1$

con n natural eran números primos (después de todo, los cinco primeros términos, 3 (n=0), 5 (n=1), 17 (n=2), 257 (n=3) y 65537 (n=4) lo son), pero Euler probó que no era así en 1732. En efecto, al tomar n=5 se obtiene un número compuesto:

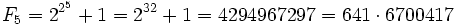
$F_{5} = 2^{2^5} + 1 = 2^{32} + 1 = 4 294 967 297 = 641 \cdot 6 700 417 \;$

4294967297 es el número más pequeño que, siendo número de Fermat, no es primo.

Actualmente, sólo se conocen cinco números primos de Fermat, que son los que ya se conocían en tiempos del propio Fermat, y, a fecha de agosto de 2008 sólo se conoce la factorización completa de los doce primeros números de Fermat (desde n=0 hasta n=11). Estas son algunas de las conjeturas que existen hoy día sobre estos números:

¿Sólo hay cinco números primos de Fermat (3, 5, 17, 257 y 65537)?
¿Existen infinitos primos de Fermat?

Pequeño teorema de Fermat

Imagen:Pierre de Fermat.jpg

Pierre de Fermat.

El pequeño teorema de Fermat es uno de los teoremas clásicos de teoría de números relacionado con la divisibilidad. Se formula de la siguiente manera:

{{{titulo}}}

Si p es un número primo, entonces, para cada número natural a coprimo con p , a^p-1 ≡ 1 (mod p) O equivalentemente: Si p es un número primo, entonces, para cada número natural a , a^p ≡ a (mod p)

Demostración:

{{{demo}}}

Esto quiere decir que, si se eleva un número a a la p-ésima potencia y al resultado se le resta a, lo que queda es divisible por p (véase aritmética modular). Su interés principal está en su aplicación al problema de la primalidad y en criptografía.

Alrededor de 1636, Fermat enunció el teorema. Aparece en una de sus cartas a su confidente Frénicle de Bessy, fechada el 18 de octubre de 1640, con el siguiente texto:

p divide a a^p-1 - 1 cuando p sea primo y a sea coprimo con p.

Aunque actualmente lo conozcamos como pequeño teorema de Fermat, lo cierto es que hasta el siglo XX fue conocido como teorema de Fermat, como recoge por ejemplo Gauss en su libro Disquisitiones arithmeticae. El término pequeño teorema de Fermat, tal como lo conocemos actualmente, fue usado por primera vez por el matemático alemán Kurt Hensel en 1913 en su libro Zahlentheorie.

Principio de Fermat

Plantilla:AP

Último teorema de Fermat

Libros

El enigma de Fermat. Simon Singh. ISBN 84-08-02375-6.
El último teorema de Fermat.Simon Singh. ISBN 958-04-4865-5
Fermat: el mago de los números. Blas Torrecillas Jover. ISBN 84-930719-2-7.

Video

Video: Fermat, el margen más famoso de la historia (22´)

Sinopsis:

A principios de siglo XVII un abogado, aficionado a las matemáticas va a lanzar una serie de retos, basados en los números más simples, los enteros, a toda la comunidad matemática. Es Pierre de Fermat. La inspiración para estos retos la encontró en un antiguo libro de matemáticas escrito allá por el siglo III, la Aritmética de Diofanto. En uno de sus márgenes Fermat va a escribir una frase que se convertirá en una de las más atractivas de la historia de las matemáticas. Su famoso último teorema:

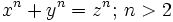“No existen soluciones enteras para la ecuación $x^n + y^n = z^n; \,n > 2$ ”

Fermat afirma que había encontrado la demostración pero por desgracia no le cabe el margen. Una desgracia que ha traído en jaque a los mejores matemáticos durante más de 350 años. Haremos un recorrido histórico por los intentos de demostrar este teorema a lo largo de tres siglos y presentaremos a Wiles, un matemático inglés que en 1994 pasó a la historia… Por fin alguien había conseguido demostrar el “ultimo teorema de Fermat”

Obtenido de "http://maralboran.org/wikipedia/index.php/Fermat"

Categorías: Matemáticas | Historia de las Matemáticas | Matemáticos

 {{teorema
-|1=Si ''p'' es un número primo, entonces, para cada número natural ''a'' , ''a''<sup>p</sup> ≡ ''a'' (mod ''p'')
+|título=Pequeño Teorema de Fermat  [Pierre de Fermat (1636)]
-|2=[[Pierre de Fermat]], 1636
+|enunciado=Si ''p'' es un número primo, entonces, para cada número natural ''a'' coprimo con ''p'' , ''a''<sup>p-1</sup> ≡ 1 (mod ''p'')
-}}
+O equivalentemente:
+Si ''p'' es un número primo, entonces, para cada número natural ''a'' , ''a''<sup>p</sup> ≡ ''a'' (mod ''p'')
-Aunque son equivalentes, el teorema suele ser presentado de esta otra forma:
-{{teorema
-|1=Si ''p'' es un número primo, entonces, para cada número natural ''a'' coprimo con ''p'' , ''a''<sup>p-1</sup> ≡ 1 (mod ''p'')
-|2=Pierre de Fermat, 1636
 }}
 -->
 Esto quiere decir que, si se eleva un número ''a'' a la ''p''-ésima potencia y al resultado se le resta ''a'', lo que queda es divisible por ''p'' (véase aritmética modular).  Su interés principal está en su aplicación al problema de la primalidad y en criptografía.
+Alrededor de 1636, Fermat enunció el teorema. Aparece en una de sus cartas a su confidente Frénicle de Bessy, fechada el 18 de octubre de 1640, con el siguiente texto:
+<center>''p'' divide a ''a''<sup>p-1</sup> - 1 cuando ''p'' sea primo y ''a'' sea coprimo con ''p''.</center>
+Aunque actualmente lo conozcamos como ''pequeño teorema de Fermat'', lo cierto es que hasta el siglo XX fue  conocido como ''teorema de Fermat'', como recoge por ejemplo [[Gauss]] en su libro ''Disquisitiones arithmeticae''. El término ''pequeño teorema de Fermat'', tal como lo conocemos actualmente, fue usado por primera vez por el matemático alemán Kurt Hensel en 1913 en su libro ''Zahlentheorie''.
 === Principio de Fermat ===