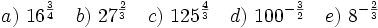Raíces y Radicales (4ºESO Académicas)
De Wikipedia
| Revisión de 18:57 9 ene 2009 Coordinador (Discusión | contribuciones) (→Radicales) ← Ir a diferencia anterior |
Revisión de 19:12 9 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Raíces== | + | =Raíces= |
| - | ===Definición=== | + | ==Definición== |
| Sabemos que <math>3^2 = 9\;\!</math>. Esta igualdad la podemos expresar de forma similar como <math>\sqrt{9}=3</math> y se lee "3 es igual a la raíz cuadrada de 9". | Sabemos que <math>3^2 = 9\;\!</math>. Esta igualdad la podemos expresar de forma similar como <math>\sqrt{9}=3</math> y se lee "3 es igual a la raíz cuadrada de 9". | ||
| Línea 35: | Línea 35: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades=== | + | ==Propiedades== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| *<math>\sqrt[n]{1}=1</math> y <math>\sqrt[n]{0}=0</math>, para cualquier valor del índice <math>n\;\!</math>. | *<math>\sqrt[n]{1}=1</math> y <math>\sqrt[n]{0}=0</math>, para cualquier valor del índice <math>n\;\!</math>. | ||
| Línea 60: | Línea 60: | ||
| }} | }} | ||
| - | ===Raíces exactas e inexactas=== | + | ==Raíces exactas e inexactas== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Se llaman '''raíces exactas''' a aquellas que dan como resultado un número racional. En caso contrario diremos que son '''inexactas''' y el resultaado será un número irracional.{{p}} | Se llaman '''raíces exactas''' a aquellas que dan como resultado un número racional. En caso contrario diremos que son '''inexactas''' y el resultaado será un número irracional.{{p}} | ||
| Línea 93: | Línea 93: | ||
| }}{{p}} | }}{{p}} | ||
| - | ===La raíz como potencia de exponente fraccionario=== | + | ==La raíz como potencia de exponente fraccionario== |
| {{Teorema| | {{Teorema| | ||
| titulo=Proposición | titulo=Proposición | ||
| Línea 145: | Línea 145: | ||
| {{p}} | {{p}} | ||
| - | ==Radicales== | + | =Radicales= |
| - | ===Definición=== | + | ==Definición== |
| {{Caja_Amarilla|texto=Se llama '''radical''' a cualquier expresión en la que aparezcan raíces}} | {{Caja_Amarilla|texto=Se llama '''radical''' a cualquier expresión en la que aparezcan raíces}} | ||
| {{p}} | {{p}} | ||
| - | ===Operaciones básicas con radicales=== | + | ==Operaciones básicas con radicales== |
| {{p}} | {{p}} | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Línea 227: | Línea 227: | ||
| {{p}} | {{p}} | ||
| - | ===Suma y resta de radicales con el mismo índice y radicando=== | + | ==Suma y resta de radicales con el mismo índice y radicando== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| '''Para sumar y restar radicales, éstos deben tener el mismo radicando y el mismo índice. | '''Para sumar y restar radicales, éstos deben tener el mismo radicando y el mismo índice. | ||
| Línea 239: | Línea 239: | ||
| {{p}} | {{p}} | ||
| - | ===Extracción e introducción de factores en un radical=== | + | ==Extracción e introducción de factores en un radical== |
| - | ====Extracción de factores==== | + | ===Extracción de factores=== |
| {{Caja_Amarilla|texto=Para extaer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto. | {{Caja_Amarilla|texto=Para extaer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto. | ||
| {{p}} | {{p}} | ||
| Línea 255: | Línea 255: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ====Introducción de factores==== | + | ===Introducción de factores=== |
| {{Caja_Amarilla|texto=Para introducir factores dentro de un radical se multiplica el exponente del factor por el índice del radical. | {{Caja_Amarilla|texto=Para introducir factores dentro de un radical se multiplica el exponente del factor por el índice del radical. | ||
| {{p}} | {{p}} | ||
| Línea 286: | Línea 286: | ||
| }} | }} | ||
| - | ===Suma y resta de radicales con el mismo índice y distinto radicando=== | + | ==Suma y resta de radicales con el mismo índice y distinto radicando== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando: | Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando: | ||
| Línea 317: | Línea 317: | ||
| }} | }} | ||
| - | ===Producto y cocientes de radicales de distinto índice=== | + | ==Producto y cocientes de radicales de distinto índice== |
| {{Caja_Amarilla|texto=Para multiplicar o dividir radicales con distintos índices, éstos deben tener el mismo radicando. En tal caso, los radicales los convertimos en potencias de la misma base y operamos con ellas, para obtener una única potencia, que posemos volver a poner en forma radical. | {{Caja_Amarilla|texto=Para multiplicar o dividir radicales con distintos índices, éstos deben tener el mismo radicando. En tal caso, los radicales los convertimos en potencias de la misma base y operamos con ellas, para obtener una única potencia, que posemos volver a poner en forma radical. | ||
| {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| Línea 326: | Línea 326: | ||
| (Otro método: [http://maralboran.org/web_ma/descartes/3_eso/Radicales/radicales6.htm sin pasar a potencia de exponente fraccionario]. Ver también: [http://maralboran.ath.cx/web_ma/descartes/3_eso/Radicales/radicales5.htm Radicales equivalentes]) | (Otro método: [http://maralboran.org/web_ma/descartes/3_eso/Radicales/radicales6.htm sin pasar a potencia de exponente fraccionario]. Ver también: [http://maralboran.ath.cx/web_ma/descartes/3_eso/Radicales/radicales5.htm Radicales equivalentes]) | ||
| - | ===Racionalización de denominadores=== | + | ==Racionalización de denominadores== |
| {{Caja_Amarilla|texto=El procedimiento por el cual hacemos desaparecer las raíces de los denominadores se le llama '''racionalización'''}} | {{Caja_Amarilla|texto=El procedimiento por el cual hacemos desaparecer las raíces de los denominadores se le llama '''racionalización'''}} | ||
| - | ====Caso 1: Denominador con raíces cuadradas==== | + | ===Caso 1: Denominador con raíces cuadradas=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Para racionalizar uno de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma. | Para racionalizar uno de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma. | ||
| Línea 351: | Línea 351: | ||
| }} | }} | ||
| - | ====Caso 2: Denominador con otras raíces==== | + | ===Caso 2: Denominador con otras raíces=== |
| {{Caja_Amarilla|texto=Las cantidades exponenciales del radical para multiplicar al numerador y denominador de la fracción será el número del exponente que falta para acercarse al índice del radical. En caso de que el exponente sea mayor que el índice de la raíz, la cantidad de aquel exponente será la que falte para llegar al múltiplo más cercano de la raíz. | {{Caja_Amarilla|texto=Las cantidades exponenciales del radical para multiplicar al numerador y denominador de la fracción será el número del exponente que falta para acercarse al índice del radical. En caso de que el exponente sea mayor que el índice de la raíz, la cantidad de aquel exponente será la que falte para llegar al múltiplo más cercano de la raíz. | ||
| Línea 369: | Línea 369: | ||
| }} | }} | ||
| - | ====Caso 3: Denominador con sumas y restas de raíces==== | + | ===Caso 3: Denominador con sumas y restas de raíces=== |
| {{Caja_Amarilla|texto=Se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión) | {{Caja_Amarilla|texto=Se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión) | ||
Revisión de 19:12 9 ene 2009
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Raíces
Definición
Sabemos que 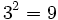 . Esta igualdad la podemos expresar de forma similar como
. Esta igualdad la podemos expresar de forma similar como 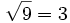 y se lee "3 es igual a la raíz cuadrada de 9".
y se lee "3 es igual a la raíz cuadrada de 9".
- Se define la raíz cuadrada de un número
 como otro número
como otro número  tal que
tal que 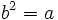 .
.
Y escribimos:
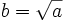
- Se define la raíz cúbica de un número
 como otro número
como otro número  tal que
tal que 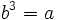 .
.
Y escribimos:
![b=\sqrt[3]{a}](/wikipedia/images/math/6/0/0/60067ca3ef9f9cd5db25de80fbfcb000.png)
- Igualmente, se define raíz n-sima de un número
 como otro número
como otro número  tal que
tal que 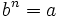 .
. 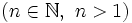
Y escribimos:
![b=\sqrt[n]{a}](/wikipedia/images/math/c/e/0/ce05f9d287d25fe0a5fd8e680bd177f5.png)
El número  se llama radicando, el número
se llama radicando, el número  , índice y
, índice y  es la raíz.
es la raíz.
Propiedades
![\sqrt[n]{1}=1](/wikipedia/images/math/f/2/3/f2301fcbef74b110ad8d373f2b32a16b.png) y
y ![\sqrt[n]{0}=0](/wikipedia/images/math/8/6/5/865db751c6cb2e12533fccdf8de1e1df.png) , para cualquier valor del índice
, para cualquier valor del índice  .
.
- Si
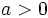 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) existe cualquiera que sea el índice
existe cualquiera que sea el índice  .
.
- Si
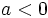 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) sólo existe si el índice
sólo existe si el índice  es impar.
es impar.
- Si el índice
 es par y el radicando
es par y el radicando 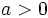 , la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto. Si el índice es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando
, la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto. Si el índice es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando  .
.
![\sqrt[3]{1}=1](/wikipedia/images/math/d/5/3/d53d30c7123945d21786c0fb38eeeb18.png) .
.
![\sqrt[5]{0}=0](/wikipedia/images/math/e/9/5/e95b8cee4e9e352608032036b0bd68d7.png) .
.
![\sqrt[4]{16}=\pm 2](/wikipedia/images/math/3/5/c/35cc75069a6350b569ad8c8f72bf6ae2.png) porque
porque 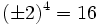 .
.
![\sqrt[3]{64}=4](/wikipedia/images/math/f/2/4/f2482a82a1ce97518a3bbef09d9575b5.png) porque
porque 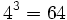 .
.
![\sqrt[3]{-8}=-2](/wikipedia/images/math/1/5/4/154ab22db729e6b6490caa36d8669830.png) porque
porque 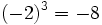 .
.
![\sqrt[4]{-8}= no \ existe](/wikipedia/images/math/a/2/1/a21d3d89fedd78f5c9a6378b3cf240f3.png) porque ningún número elevado a 4 puede dar negativo (-8).
porque ningún número elevado a 4 puede dar negativo (-8).
Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno:
Raíces exactas e inexactas
Para que una raíz sea exacta, al descomponer el radicando en factores primos, las potencias de éstos deben ser todas números divisibles por el índice.
Ejemplo: Raíces exactas e inexactas
- Calcula las siguientes raíces cuando sean exactas:
a) Descomponemos 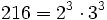 .
.
Como las potencias son divisibles por 3, la raíz es exacta. Para obtenerla, dividimos cada exponente entre el índice:
![\sqrt[3]{216}=\sqrt[3]{2^3 \cdot 3^3}=2^{\frac{3}{3}} \cdot 3^{\frac{3}{3}}=2^1 \cdot 3^1=6](/wikipedia/images/math/4/a/b/4ab09f3247f4181f74270a6db537c4a3.png)
Luego ![\sqrt[3]{216}](/wikipedia/images/math/2/a/6/2a60cb9da80e1f9abad0623c37ccfb67.png) es racional.
es racional.
b) Descomponemos 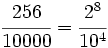 .
.
Como las potencias son divisibles por 4, la raíz es exacta. Para obtenerla, dividimos cada exponente entre el índice:
![\sqrt[4]{0'0256}=\sqrt[4]{\cfrac{256}{10000}}=\sqrt[4]{\cfrac {2^8}{10^4}}=\cfrac {2^{\frac{8}{4}}}{10^{\frac{4}{4}}}=\cfrac{2^2}{10^1}=\cfrac{4}{10}=0'4](/wikipedia/images/math/9/7/1/971bba665f246bea65b83612ca682e78.png)
Luego ![\sqrt[4]{0'0256}](/wikipedia/images/math/5/3/e/53e9b60b9676b9839103c0b91278c19b.png) es racional.
es racional.
c) Descomponemos 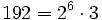 .
.
La potencia de 3 es 1, que no es divisible por 3. Por tanto, la raíz no es exacta.
Luego![\sqrt[3]{192}](/wikipedia/images/math/b/d/f/bdfe841e1073096ee42922125fc7e19d.png) es irracional.
es irracional.La raíz como potencia de exponente fraccionario
Proposición
- Toda raíz se puede expresar como una potencia cuya base es el radicando,
 , y el exponente es
, y el exponente es 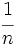 , siendo
, siendo  el índice de la raíz. Ésto es:
el índice de la raíz. Ésto es:
|
|
- De forma similar, también se cumple:
|
|
Para la primera parte, basta con ver que se cumple la condición de la definición de raíz.
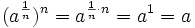
Para la segunda parte, haremos una comprobación análoga:
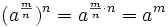
Pulsa el botón "Ejemplo" para ver distintos ejemplos y anótalos en tu cuaderno:
Ejemplo: La raíz como potencia de exponente fraccionario
- Escribe las siguientes potencias de exponente fraccionario en forma de raíces y calcula su valor:
Utiliza la siguiente escena para comprobar su resultado. Aumenta el número de decimales cuando sea necesario.
Propiedades: Las potencias con exponente fraccionario tienen las mismas propiedades que con exponente natural o entero.
Radicales
Definición
Se llama radical a cualquier expresión en la que aparezcan raíces
Operaciones básicas con radicales
Para multiplicar radicales del mismo índice se deja el índice y se multiplican los radicandos
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Cociente:
Para dividir radicales del mismo índice, se deja el índice y se dividen los radicandos.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Potencia:
Para elevar un radical a una potencia se eleva el radicando a dicha potencia, manteniendo el índice.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Radical:
Para hallar el radical de un radical se multiplican los índices de ambos.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
|
Actividad Interactiva: Radicales
Actividad 1. Operaciones con radicales del mismo índice.
Actividad: Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien. |
Suma y resta de radicales con el mismo índice y radicando
Para sumar y restar radicales, éstos deben tener el mismo radicando y el mismo índice.
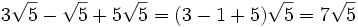
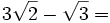 (No se puede simplificar)
(No se puede simplificar)
![3\sqrt[3]{2}+\sqrt{2}=](/wikipedia/images/math/a/6/e/a6edb4be927bfe44dff1ae00ac0eb772.png) (No se puede simplificar)
(No se puede simplificar)
Extracción e introducción de factores en un radical
Extracción de factores
Para extaer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Introducción de factores
Para introducir factores dentro de un radical se multiplica el exponente del factor por el índice del radical.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
|
Actividad Interactiva: Introducción y extracción de factores de un radical
Actividad 1. Introduce y extráe factores de radicales.
Actividad: Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien. |
Suma y resta de radicales con el mismo índice y distinto radicando
Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando:
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
|
Actividad Interactiva: Suma y resta de radicales
Actividad 1. Suma y resta radicales con el mismo índice y distinto radicando.
Actividad: Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien. |
Producto y cocientes de radicales de distinto índice
Para multiplicar o dividir radicales con distintos índices, éstos deben tener el mismo radicando. En tal caso, los radicales los convertimos en potencias de la misma base y operamos con ellas, para obtener una única potencia, que posemos volver a poner en forma radical.
![3\sqrt[3]{5} \cdot \sqrt[4]{5}:\sqrt{5}=3\cdot5^{\frac{1}{3}}\cdot5^{\frac{1}{4}}:5^{\frac{1}{2}}=3\cdot5^{(\frac{1}{3}+\frac{1}{4}-\frac{1}{2})}=3\cdot5^\frac{1}{12}=3\sqrt[12]{5}](/wikipedia/images/math/b/1/a/b1a9fbc1341d8f63d5659188b2def312.png)
![3\sqrt[5]{2}-\sqrt[3]{3}=](/wikipedia/images/math/2/d/6/2d6ed3298d1c8572ad52fb6df78ce017.png) (No se puede simplificar)
(No se puede simplificar)
(Otro método: sin pasar a potencia de exponente fraccionario. Ver también: Radicales equivalentes)
Racionalización de denominadores
El procedimiento por el cual hacemos desaparecer las raíces de los denominadores se le llama racionalización
Caso 1: Denominador con raíces cuadradas
Para racionalizar uno de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.
Vamos a racionalizar 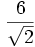
En este caso hay que multiplicar numerador y denominador por 
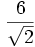 ·
· 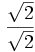 =
= 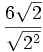
Después se despeja la raíz cuadrada del denominador:
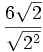 =
= 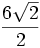
El resultado del ejercicio es éste, aunque se puede simplificar el número entero del numerador entre el del denominador, así:
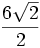 =
= 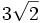
Caso 2: Denominador con otras raíces
Las cantidades exponenciales del radical para multiplicar al numerador y denominador de la fracción será el número del exponente que falta para acercarse al índice del radical. En caso de que el exponente sea mayor que el índice de la raíz, la cantidad de aquel exponente será la que falte para llegar al múltiplo más cercano de la raíz.
Vamos a racionalizar ![\frac{{2}}{\sqrt[5]{a^3b^4}}](/wikipedia/images/math/5/3/3/533185378740f77c6d3da802a18e1fdd.png)
En este ejemplo, hay que multiplicar por ![\sqrt[5] {a^2b}](/wikipedia/images/math/3/d/5/3d57844c30135fee650c9bcfd98d40d1.png) , ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz.
, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz.
Ahora, se procede a multiplicar el numerador y el denominador:
![\frac{{2}}{\sqrt[5]{a^3b^4}}](/wikipedia/images/math/5/3/3/533185378740f77c6d3da802a18e1fdd.png) ·
· ![\frac{\sqrt[5] {a^2b} }{\sqrt[5]{a^2b}}](/wikipedia/images/math/f/3/f/f3f1db7b06562f7cc5f0b7382069273e.png) =
= ![\frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}}](/wikipedia/images/math/4/e/0/4e0ba3929c6a87cfe18f62280d4d0130.png)
Ahora, se procede al despeje de las raíces, en el ejemplo de índice 5:
![\frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}}](/wikipedia/images/math/4/e/0/4e0ba3929c6a87cfe18f62280d4d0130.png) =
= ![\frac{{2\sqrt[5]{a^2b}}}{{ab}}](/wikipedia/images/math/1/9/a/19a8e793ecc8f20820460f489be0b1d0.png)
Caso 3: Denominador con sumas y restas de raíces
Se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión)
Vamos a racionalizar 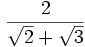
En este caso hay que multiplicar el numerador y el denominador por 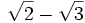 ; este resultado es el que da el producto notable de los binomios conjugados.
; este resultado es el que da el producto notable de los binomios conjugados.
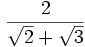 ·
· 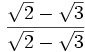 =
= 
Ahora, se procede al despeje de las raíces cuadradas del denominador:
 =
= 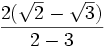 =
= 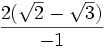 =
= 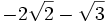
![a) \sqrt[3]{216} \quad b) \sqrt[4]{0'0256}\quad c) \sqrt[3]{192}](/wikipedia/images/math/2/6/b/26bc1ddea3425faad31fbcf8d5d86539.png)
![\sqrt[n]{a}=a^\frac{1}{n}](/wikipedia/images/math/2/0/0/2009af813099ac7b1bef0f0fb92a7999.png)
![\sqrt[n]{a^m}=a^\frac{m}{n}](/wikipedia/images/math/3/b/0/3b0234682d54453ceee722e89c782c2e.png)