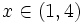Plantilla:Inecuaciones cuadráticas con una incógnita
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:44 19 ene 2009 Coordinador (Discusión | contribuciones) (→Método gráfico de resolución) ← Ir a diferencia anterior |
Revisión de 19:03 19 ene 2009 Coordinador (Discusión | contribuciones) (→Método gráfico de resolución) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/4b_eso/Inecuaciones/ineccuad_1.html | + | url=http://maralboran.org/web_ma/descartes/4b_eso/Inecuaciones/inec2_1inc_1.html |
| width=500 | width=500 | ||
| height=410 | height=410 | ||
Revisión de 19:03 19 ene 2009
- Una inecuación cuadrática con una incógnita es una inecuación con una incógnita en la que las expresiones algebraicas que aparecen son de tipo cuadrático, es decir, de la forma
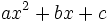 .
.
Método gráfico de resolución
El método gráfico requiere que el miembro de la derecha de la inecuación sea cero, lo cual siempre se puede conseguir mediante transformaciones.
Ejemplo: Inecuaciones cuadráticas con una incógnita
Resuelve la siguiente inecuación:
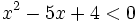
Solución:
Representamos la parábola 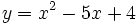 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa).
En realidad basta hallar los puntos de corte con el eje X y determinar la dirección de las ramas a partir del signo del coeficiente de 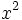 .
.
En este caso, los puntos de corte son 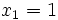 y
y 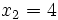 , soluciones de la ecuación de segundo grado
, soluciones de la ecuación de segundo grado
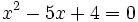
y las ramas va hacia arriba porque el coeficiente de 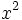 es positivo.
es positivo.