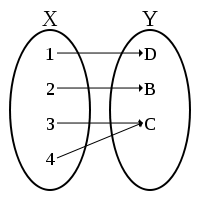
Función sobreyectiva
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:13 24 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:13 24 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| {{p}} | {{p}} | ||
| <center><math>\forall y\in Y : \exists x\in X \ / \ f(x) = y</math></center> | <center><math>\forall y\in Y : \exists x\in X \ / \ f(x) = y</math></center> | ||
| - | + | {{p}} | |
| Es decir, una función <math>f\;</math> es '''sobreyectiva'''si <math>Im_f=Y\;</math> | Es decir, una función <math>f\;</math> es '''sobreyectiva'''si <math>Im_f=Y\;</math> | ||
| }} | }} | ||
Revisión de 18:13 24 ene 2009
Una función 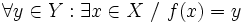 Es decir, una función |
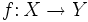 es sobreyectiva, suprayectiva o exhaustiva si todo valor de
es sobreyectiva, suprayectiva o exhaustiva si todo valor de 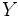 se corresponde con un valor de
se corresponde con un valor de 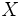 . Simbólicamente:
. Simbólicamente:
 es sobreyectivasi
es sobreyectivasi 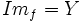
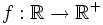 , dada por
, dada por 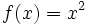 es suprayectiva.
es suprayectiva.
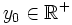 , existe el valor
, existe el valor 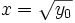 que se corresponde con él.
que se corresponde con él.