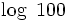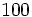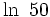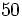Funciones logarítmicas (1ºBach)
De Wikipedia
| Revisión de 18:59 25 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:19 25 ene 2009 Coordinador (Discusión | contribuciones) (→Función logarítmica de base a) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Función logarítmica de base a== | ==Función logarítmica de base a== | ||
| + | {{Tabla75 | ||
| + | |celda2= | ||
| + | [[Imagen:Logarithms.png|thumb|364px|Representación gráfica de logaritmos en varias bases: | ||
| + | <br />el <span style="color:red">rojo</span> representa el logaritmo en base [[Número e|''e'']], | ||
| + | <br />el <span style="color:green">verde</span> corresponde a la base 10, | ||
| + | <br />y el <span style="color:purple">púrpura</span> al de la base 1,7. | ||
| + | <br />Los logaritmos de todas las bases pasan por el punto (1, 0), esto es debido a que cualquier número elevado a la cero es igual a uno, y también los puntos (''b'', 1) para la base ''b'', debido a que cualquier número elevado a la unidad es igual a sí mismo.]] | ||
| + | |celda1= | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| Línea 23: | Línea 31: | ||
| La función logarítmica de base <math>e = 2,7182...\;</math> (número e) es de especial importancia en matemáticas. Se denomina '''función logaritmo neperiano''' y se designa por <math>ln \, x</math>. | La función logarítmica de base <math>e = 2,7182...\;</math> (número e) es de especial importancia en matemáticas. Se denomina '''función logaritmo neperiano''' y se designa por <math>ln \, x</math>. | ||
| La función logarítmica de base 10 también es de particular interés. Se denomina '''función logaritmo decimal''' y se designa por <math>log \, x</math> (sin especificar la base). | La función logarítmica de base 10 también es de particular interés. Se denomina '''función logaritmo decimal''' y se designa por <math>log \, x</math> (sin especificar la base). | ||
| - | + | }} | |
| {{p}} | {{p}} | ||
| {{AI2|titulo=Actividad Interactiva: ''Función logarítmica''|cuerpo= | {{AI2|titulo=Actividad Interactiva: ''Función logarítmica''|cuerpo= | ||
| Línea 53: | Línea 61: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Propiedades== | ==Propiedades== | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
Revisión de 19:19 25 ene 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Logaritmos (1ºBach) | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Función logarítmica de base a
Sea 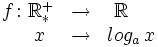 La función logarítmica de base | 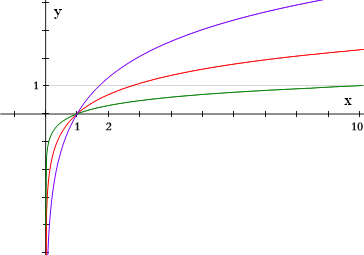 Representación gráfica de logaritmos en varias bases: el rojo representa el logaritmo en base e, el verde corresponde a la base 10, y el púrpura al de la base 1,7. Los logaritmos de todas las bases pasan por el punto (1, 0), esto es debido a que cualquier número elevado a la cero es igual a uno, y también los puntos (b, 1) para la base b, debido a que cualquier número elevado a la unidad es igual a sí mismo. |
|
Actividad Interactiva: Función logarítmica
Actividad 1. Representación gráfica de distintas funciones logarítimicas y comparación con la función exponencial con la misma base.
Actividad: En esta escena tienes las gráfica de las funciones: a)
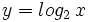 (en amarillo); b) (en amarillo); b) 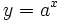 (en verde) (en verde)Cambia con los controles el valor de
|
Propiedades
Las funciones exponenciales de base  cumplen las siguientes propiedades:
cumplen las siguientes propiedades:
- Son continuas en
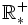 .
.
- Pasan por
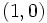 y
y 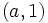 .
.
- Si
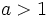 son crecientes y si
son crecientes y si 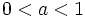 son decrecientes. Su crecimiento es menor que el de las funciones raíz de cualquier índice
son decrecientes. Su crecimiento es menor que el de las funciones raíz de cualquier índice ![\sqrt[n]{x}](/wikipedia/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) .
.
- La función logaritmica y la exponencial de la misma base son funciones inversas y por tanto sus gráficas son simétricas respecto de la recta
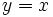 .
.
El modelo logarítmico
Ejemplo: Modelo logarítmico
Los científicos modelan la respuesta humana a estímulos (como sonido, luz o presión) por medio de funciones logarítmicas. El psicólogo Gustav Fechner formuló la ley como
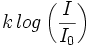
donde 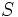 es la intensidad subjetiva del estímulo,
es la intensidad subjetiva del estímulo, 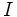 la intensida física del estímulo,
la intensida física del estímulo, 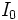 la intensidad física umbral y
la intensidad física umbral y  es una constante que difiere en cada estímulo sensorial.
es una constante que difiere en cada estímulo sensorial.
Por ejemplo, la percepción de la sonoridad 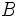 , en decibelios (dB), de un sonido con intensidad física
, en decibelios (dB), de un sonido con intensidad física 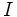 en W / m2 está dada por
en W / m2 está dada por
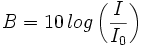
donde 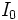 la intensidad física de un sonido apenas audible (umbral). Encuentra el nivel de sonoridad (en dB) de un sonido cuya intensidad física
la intensidad física de un sonido apenas audible (umbral). Encuentra el nivel de sonoridad (en dB) de un sonido cuya intensidad física 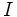 es 100 veces la de
es 100 veces la de 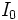 .
.
Partimos del hecho de que 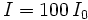 , entonces, sustituyendo en la fórmula de la percepción sonora, tendremos:
, entonces, sustituyendo en la fórmula de la percepción sonora, tendremos:
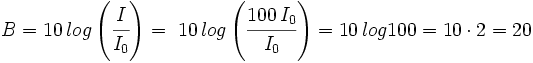
Calculadora
Logartitmo decimal
|
Calculadora: Logaritmo decimal |
Logartitmo neperiano
|
Calculadora: Logaritmo neperiano |
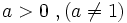 un número real. Se define la función logarítmica de base
un número real. Se define la función logarítmica de base 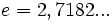 (número e) es de especial importancia en matemáticas. Se denomina función logaritmo neperiano y se designa por
(número e) es de especial importancia en matemáticas. Se denomina función logaritmo neperiano y se designa por 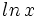 .
La función logarítmica de base 10 también es de particular interés. Se denomina función logaritmo decimal y se designa por
.
La función logarítmica de base 10 también es de particular interés. Se denomina función logaritmo decimal y se designa por 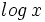 (sin especificar la base).
(sin especificar la base).