Funciones: Definición (1ºBach)
De Wikipedia
| Revisión de 18:55 1 feb 2009 Coordinador (Discusión | contribuciones) (→Videos sobre funciones) ← Ir a diferencia anterior |
Revisión de 19:03 1 feb 2009 Coordinador (Discusión | contribuciones) (→Videos sobre el dominio de definición de una función) Ir a siguiente diferencia → |
||
| Línea 90: | Línea 90: | ||
| |titulo1=Dominio de definición de una función | |titulo1=Dominio de definición de una función | ||
| |duracion=8'51" | |duracion=8'51" | ||
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis= |
| + | *Dominio de definición de una función. | ||
| + | *Interpretación gráfica del dominio. | ||
| + | *Necesidad de saber el dominio de una función. | ||
| + | *Ejemplos. | ||
| |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0134.htm | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0134.htm | ||
| }} | }} | ||
| Línea 97: | Línea 101: | ||
| |titulo1=Reglas "Sagradas" del Cálculo | |titulo1=Reglas "Sagradas" del Cálculo | ||
| |duracion=3'43" | |duracion=3'43" | ||
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis= |
| + | *Hay ciertas reglas en matemáticas que no se pueden violar. Aquí las vamos a recordar. | ||
| |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0132.htm | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0132.htm | ||
| }} | }} | ||
| Línea 104: | Línea 109: | ||
| |titulo1=De las funciones y de las serpientes | |titulo1=De las funciones y de las serpientes | ||
| |duracion=9'01" | |duracion=9'01" | ||
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis= |
| + | *Hay funciones que a la hora de trabajar con ellas no presentan ningún problema; otras sin embargo son realmente peligrosas. | ||
| |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0133.htm | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0133.htm | ||
| }} | }} | ||
| Línea 111: | Línea 117: | ||
| |titulo1=Ejemplos de "serpientes" peligrosas... o no | |titulo1=Ejemplos de "serpientes" peligrosas... o no | ||
| |duracion=14'53" | |duracion=14'53" | ||
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis= |
| + | *Ejemplos de algunas funciones "peligrosas" y de otras que no presentan ningún problema. | ||
| |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0133_01.htm | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0133_01.htm | ||
| }} | }} | ||
Revisión de 19:03 1 feb 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Función real de variable real
Una función real de variable real,  , es una correspondencia entre números reales que asocia a cada valor de la variable independiente
, es una correspondencia entre números reales que asocia a cada valor de la variable independiente  un único valor de la variable dependiente
un único valor de la variable dependiente  .
.
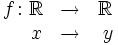
En tal caso decimos que  es función de
es función de  y lo representamos por
y lo representamos por  .
.
Explicación de la notación  . Ejemplos.
. Ejemplos.
- Definición de función, variable independiente y variable dependiente. Ejemplos
- Definición de función algebraica y de función trascendente. Ejemplos.
Gráfica de una función
Necesidad de la representación gráfica de una función. Ejemplos.
|
Actividades Interactivas: Funciones
1. Determina si son o no son funciones las siguientes gráficas.
Actividad: Una función es una relación entre dos variables numéricas, habitualmente las denominamos  (variable independiente) e (variable independiente) e  (variable dependiente); Se le llama variable dependiente porque su valor depende del valor de la otra que llamamos independiente. (variable dependiente); Se le llama variable dependiente porque su valor depende del valor de la otra que llamamos independiente.
Pero además, para que una relación sea función, a cada valor de la variable independiente le corresponde uno y sólo un valor de la variable dependiente, no le pueden corresponder dos o más valores. a) Observa en la escena las gráficas y di cuál de ellas es función y por qué no lo es la otra. Observa al mover el punto P cuántos puntos de corte tiene la recta azul con cada gráfica; si es más de uno no es una función. |
Operaciones con funciones
- Definición de las distintas operaciones que se pueden realizar con funciones. Ejemplos.
Dominio e imagen de una función
- El conjunto de valores de la variable independiente,
 , para los que hay un valor de la variable dependiente,
, para los que hay un valor de la variable dependiente,  , se llama dominio de definición de la función. Se denota
, se llama dominio de definición de la función. Se denota 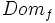 .
.
- El conjunto de valores que toma la variable independiente,
 , se llama imagen, recorrido o rango de la función. Se denota
, se llama imagen, recorrido o rango de la función. Se denota 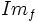 .
.
- Si un punto (x,y) pertenece a la gráfica de la función entonces se dice que y es la imagen de x y también que x es la antiimagen de y.
"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
- t = "Tiempo que está abierto el grifo".
- V = "Volumen de agua que se ha llenado el depósito".
- Dominio: El tiempo que el grifo puede estar abierto es un número que varía entre 0 segundos y 100 segundos:
![Dom_f=[0,100]\;](/wikipedia/images/math/a/b/d/abd624243bc89fe5a2233724f02b4f4a.png)
- Recorrido: El volumen de agua que se ha llenado el depósito es un número que varía ente 0 litros y 200 litros:
![Im_f=[0,200]\;](/wikipedia/images/math/3/9/f/39fa0225481adedcbe46a7b134738d1a.png)
Tutorial en el que se explica el cálculo del dominio y la imagen de una función a partir de su gráfica.
Halla el dominio de una función a partir de su gráfica:
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Estudio del dominio de una función a partir de su gráfica.
Halla la imagen de una función a partir de su gráfica:
Estudio del recorrido o imagen de una función a partir de su gráfica.
Estudio del recorrido o imagen de una función a partir de su gráfica.
Estudio del recorrido o imagen de una función a partir de su gráfica.
Estudio del recorrido o imagen de una función a partir de su gráfica.
Halla el dominio de una función a partir de un enunciado:
Pati tiene una hermosa planta. La planta empezó a retoñar 2 días antes de que Pati la comprara, y la tuvo por 98 días antes de que muriera. La altura máxima que alcanzó a planta fue de 30 cm. Si denotamos por h(t) la altura de la planta en cm tras transcurrir t días desde el día de la compra, indica qué conjunto numérico es el más adecuado para el dominio de la función: ¿los números enteros o los números reales?. Halla el dominio.
Thomas tiene 400 barras de caramelo en su tienda, y cada una cuesta $0.50. Sea p(b) el precio, medido en pesos ($), de la compra de b barras de caramelo. Indica qué conjunto numérico es el más adecuado para el dominio de la función: ¿los números enteros o los números reales?. Halla el dominio.
Mason está parado en el 5º escalón de una escalera vertical. La escalera tiene 15 escalones y la diferencia de altura entre escalones consecutivos es de 0.5 m. Él está pensando si sube, baja o se queda quieto. Sea h(n) la altura por encima del nivel del suelo de los pies de Mason (medido en metros) después de moverse n escalones (si Mason bajara n escalones , n es negativa). Indica qué conjunto numérico es el más adecuado para el dominio de la función: ¿los números enteros o los números reales?. Halla el dominio.
Imagen y antiimagen:
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Cálculo de la imagen y de la antiimagen a partir de la gráfica de una función.
Dada la gráfica de la función g(x), halla la antiimagen de -2, es decir, el valor de x para el cual g(x) = -2.
Dada la gráfica de la función f(x), halla el valor de x, además de -5, para el cual f(x) = f(-5).
Dada la función f(t) = -2t + 5, halla la antiimagen de 13, es decir, el valor de t para el cual f(t) = 13.
Actividades en las que aprenderás de forma visual los conceptos de dominio y recorrido de una función.
Observa la escena y mueve el punto P para ver los valores que recorren las variables:
Suponiendo que la gráfica se comporta de forma análoga a lo largo de todo el eje X, ¿Cuál es su dominio y su imagen?
Observa la escena y mueve el punto P para ver los valores que recorren las variables:
¿Cuál es su dominio y su imagen?
Observa la escena y mueve el punto P para ver los valores que recorren las variables:
¿Cuál es su dominio y su imagen?
En esta escena podrás visualizar el dominio y la imagen de una función. Podrás elegir entre un tramo de recta (función lineal) o de parábola (función cuadrática).
Dominio y rango a partir de gráficas.
Dominio de una función dada por un enunciado.
Imagen y antiimagen:
Actividades con las que aprenderás los conceptos de imagen y antiimagen.
Halla la antiimagen utilizando la gráfica de la función.
Halla la antiimagen utilizando la expresión analítica de la función.
|
Actividad: Dominio e imagen de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Determinación del dominio de una función
El dominio de una función puede estar determinado o limitado por diferentes razones:
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
(Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, el lado no puede tomar valores negativos)
- Por voluntad de quien propone la función (A veces nos puede interesar estudiar sólo un trozo de la función).
Ejemplos: Dominio de una función dada por una expresión analítica
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
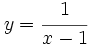
- b)
- c)
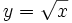
- c)
- d)
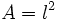 (Área de un cuadrado de lado
(Área de un cuadrado de lado 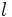 )
)
- d)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de  válido.
válido.
- b) Su dominio es
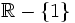 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
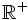 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
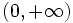 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
Intervalos. Notación.
Dominio de una función.
Rango o imagen de una función.
Conceptos de dominio y rango de una función. Ejemplos
Dominio y rango de una función. Ejemplos.
Halla el dominio de 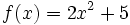 .
.
Halla el dominio de 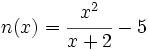 .
.
Halla el dominio de 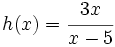 .
.
Halla el dominio de 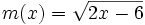 .
.
Halla el dominio de 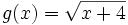 .
.
Halla el dominio de 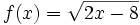 .
.
Dominio de una función dada por su expresión analítica.
Videos
Videos sobre el dominio de definición de una función
- Dominio de definición de una función.
- Interpretación gráfica del dominio.
- Necesidad de saber el dominio de una función.
- Ejemplos.
- Hay ciertas reglas en matemáticas que no se pueden violar. Aquí las vamos a recordar.
- Hay funciones que a la hora de trabajar con ellas no presentan ningún problema; otras sin embargo son realmente peligrosas.
- Ejemplos de algunas funciones "peligrosas" y de otras que no presentan ningún problema.
Ejemplos: Dominio de definición de una función
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
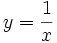 .
.

