Valor absoluto de una función (1ºBach)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 09:48 27 ene 2009
Coordinador (Discusión | contribuciones)
(→30px{{b}}Video-Ejercicios)
← Ir a diferencia anterior		 Revisión actual
Coordinador (Discusión | contribuciones)

Línea 6: Línea 6:
}} }}
{{p}} {{p}}
-==Función valor absoluto==+{{Valor absoluto de una función (1ºBach)}}
-{{Tabla50|celda1=+
-{{Caja_Amarilla|texto=La función '''valor absoluto''' es aquella que a cada número <math>x\;</math> le asigna su [[Valor absoluto (1ºBach)|valor absoluto]]. Es decir:+
-{{b}}+
-<center><math>|x|=\begin{cases} \ \ \, x & si \ \ x \ge 0+
-\\+
--x & si \ \ x < 0+
-\end{cases}+
-</math></center>+
-{{p}}+
-}}+
-|celda2=+
-<center>[[Imagen:Funcion_valor_absoluto.png|250px]]</center>+
-}}+
- +
-==Valor absoluto de una función==+
-{{Caja_Amarilla|texto=El '''valor absoluto de una función''' se define como:+
-{{b}}+
-<center><math>|f(x)|=\begin{cases} \ \ \, f(x) & si \ \ f(x) \ge 0+
-\\+
--f(x) & si \ \ f(x) < 0+
-\end{cases}+
-</math></center>+
-}}+
-{{p}}+
-{{AI2|titulo=Actividad Interactiva: ''Valor absoluto de una función''|cuerpo=+
-{{ai_cuerpo+
-|enunciado='''Actividad 1.''' Representación gráfica del valor absoluto de una función cualquiera. +
-|actividad=+
-En esta escena tienes la gráfica de la función <math>y = -x^2 + 3\;</math>. +
- +
-El control numérico "Mostrar <math>|f(x)|\;</math>", muestra la gráfica de <math>f(x)\;</math> cuando vale 0 y la de <math>|f(x)|\;</math> cuando vale 1. Dale valor 1 a este control y observa la gráfica de la función valor absoluto de <math>y = -x^2 + 3\;</math>.+
- +
-Si deseas ver la gráfica de otras funciones y las correspondientes a su valor absoluto, introduce en la caja de edición la función que desees y no olvides pulsar "Intro" .+
-{{p}}+
-<center><iframe>+
-url=http://maralboran.org/web_ma/descartes/Analisis/funciones_definidas_oper_transf/pagina6_1.html+
-width=450+
-height=380+
-name=myframe+
-</iframe></center>+
-<center>[http://maralboran.org/web_ma/descartes\Analisis\funciones_definidas_oper_transf/pagina6_1.html '''Click''' aquí si no se ve bien la escena]</center>+
-}}+
-}}+
-{{p}}+
-==Videos sobre el valor absoluto de una función==+
-{{Video_enlace2+
-|titulo1=Valor absoluto de una función+
-|duracion=7'35"+
-|sinopsis=Video tutorial de matematicasbachiller.com+
-|url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0130.htm+
-}}+
-{{p}}+
-{{ejercicio+
-|titulo=[[Imagen:Video.gif|30px]] Video-Ejercicios: ''Valor absoluto de una función''+
-|cuerpo=+
-::*[http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0130_01.htm Ejercicio 1]+
-::*[http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0130_02.htm Ejercicio 2]+
-::*[http://www.matematicasbachiller.com/videos/cdiferencial/df_t_01/vdf0130_03.htm Ejercicio 3]+
-}}+
[[Categoría: Matemáticas]][[Categoría: Funciones]] [[Categoría: Matemáticas]][[Categoría: Funciones]]

Revisión actual

Menú:
Enlaces internos Para repasar o ampliar Enlaces externos
Indice
Descartes
Manual Casio
 WIRIS
Geogebra
Calculadoras

[editar]

Función valor absoluto

La función valor absoluto es aquella que a cada número 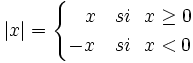x\; le asigna su valor absoluto. Es decir:  

|x|=\begin{cases} \ \ \, x & si \ \ x \ge 0 \\ -x & si \ \ x < 0 \end{cases}

Función valor absoluto     Descripción:

Representación de la función valor absoluto.

[editar]

Valor absoluto de una función

El valor absoluto de una función se define como:  

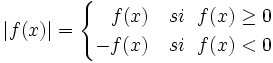
|f(x)|=\begin{cases} \ \ \, f(x) & si \ \ f(x) \ge 0 \\ -f(x) & si \ \ f(x) < 0 \end{cases}

Valor absoluto de una función (7'35")     Sinopsis:

Siendo "f" y "u" funciones reales de variable real, escribimos f = | u | si f(x) = | u(x) | .

  • La gráfica de "f" coincide con la de "u" en los puntos en que ésta toma valores no negativos.
  • En los puntos en que "u" toma valores negativos, la gráfica de "f" es simétrica de la de "u" respecto al eje de abcisas.
Valor absoluto de una función     Descripción:

Representación conjunta de una función cualquiera y su valor absoluto.

[editar]

Representación gráfica del valor absoluto de una función

ejercicio

Procedimiento

Para representar gráficamente el valor absoluto de una función f:

  1. Representamos la función f.
  2. Hacemos una simetría respecto del eje X de la parte de la gráfica de f que está por debajo de dicho eje.
  3. Borramos esa parte de f que está por debajo del eje X.
  4. La parte de la gráfica de f que está por encima del eje X la dejamos tal cual.
  5. La gráfica resultante es la gráfica del valor absoluto de f.

video
Representación gráfica del valor absoluto de una función
Ejercicio 1 (10'04")     Sinopsis:

Representa gráficamente:

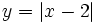
a) y=\left| x-2 \right|
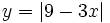
b) y=\left| 9-3x \right|
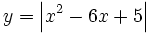
c) y=\left| x^2-6x+5 \right|
Ejercicio 2 (8'36")     Sinopsis:

Representa gráficamente:

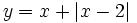
a) y=x+ \left| x-2 \right|
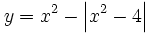
b) y=x^2 - \left| x^2-4 \right|
Ejercicio 3 (4'27")     Sinopsis:

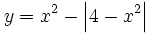
Representa gráficamente: y=x^2 - \left| 4-x^2 \right|

Ejercicio 4 (30'33")     Sinopsis:

Representa gráficamente:

a) f(x) = x + | x − 2 |
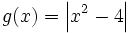
b) g(x)=\left| x^2-4 \right|
c) h(x) = | x | − x
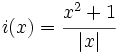
d) i(x)=\cfrac{x^2+1}{|x|}
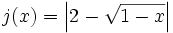
e) j(x)=\left| 2-\sqrt{1-x} \right|

Representación gráfica del valor absoluto de una función     Descripción:

Autoevaluación.

Obtenido de "http://maralboran.org/wikipedia/index.php/Valor_absoluto_de_una_funci%C3%B3n_%281%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda