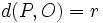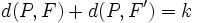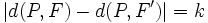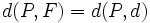Las cónicas (1ºBach)
De Wikipedia
| Revisión de 10:38 2 abr 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:46 2 abr 2009 Coordinador (Discusión | contribuciones) (→Excentricidad de una cónica) Ir a siguiente diferencia → |
||
| Línea 152: | Línea 152: | ||
| {{p}} | {{p}} | ||
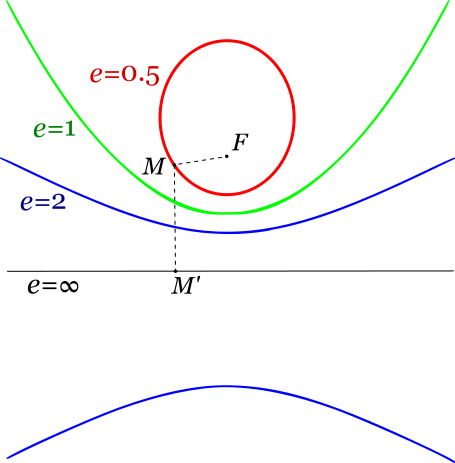
| ==Excentricidad de una cónica== | ==Excentricidad de una cónica== | ||
| - | [[Imagen:Excentricidad.jpg]] | + | [[Imagen:Excentricidad.png]] |
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 10:46 2 abr 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
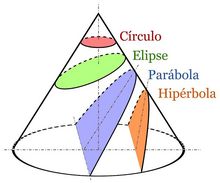
Secciones cónicas
Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. Según como corte el plano al cono tendremos (ver figura):
La primera definición de sección cónica aparece en Grecia, cerca del año 350, donde las definieron como secciones de un cono circular recto. Los nombres de hipérbola, parábola y elipse se deben a Apolonio de Pérgamo. A continuación vamos a ver definir las secciones cónicas como lugares geométricos de puntos del plano. |  |
Las cónicas como lugares geométricos
Circunferencia
La circunferencia de centro 
y radio 
, es el lugar geométrico de los puntos 
, del plano, cuya distancia al centro es .
|
|
 Actividad interactiva: Circunferncia
Actividad 1: Trazado de la circunferencia.
Actividad: Para dibujar una circunferencia sobre un papel, fijas en un punto con una chincheta el extremo de una cuerda de longitud igual al radio. En el otro extremo de la cuerda, fijas un lápiz y, manteniendo tensa la cuerda, vas trazando una línea. Activa la traza, desliza el punto P y observa.
|
Par más detalles consulta el tema de la circunferencia.
Elipse
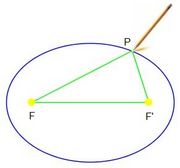
Dados dos puntos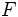 
y 
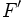llamados focos, y una distancia 
, llamada constante de la elipse (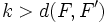
), se llama elipse al lugar geométrico de los puntos del plano cuya suma de distancias a los focos es igual a :
|
|
Actividad interactiva: Elipse
Actividad 1: Trazado de la elipse.
Actividad: 
|
Par más detalles consulta el tema de la elipse.
Hipérbola
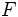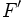Dados dos puntos y llamados focos, y una distancia , llamada constante de la hipérbola (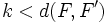
), se llama hipérbola al lugar geométrico de los puntos del plano cuya diferencia de distancias a los focos es, en valor absoluto, igual a :
|
|
Actividad interactiva: Hipérbola
Actividad 1: Trazado de la hipérbola.
Actividad: Activa la traza, desliza el punto P y observa.
|
Par más detalles consulta el tema de la hipérbola.
Parábola
Dados un punto 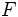llamado foco, y una recta 
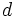, llamada directriz, se llama parábola al lugar geométrico de los puntos del plano que equidistán del foco y de la directriz:
|
|
Actividad interactiva: Parábola
Actividad 1: Trazado de la parábola.
Actividad: Activa la traza, desliza el punto P y observa.
|
Par más detalles consulta el tema de la parábola.
Excentricidad de una cónica
