Sucesos aleatorios (3ºESO)
De Wikipedia
| Revisión de 10:25 8 jun 2009 Coordinador (Discusión | contribuciones) (→Sucesos) ← Ir a diferencia anterior |
Revisión de 10:35 8 jun 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 67: | Línea 67: | ||
| ==Sucesos== | ==Sucesos== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | '''Suceso''' de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral | + | *'''Suceso''' de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral {{sube|porcentaje=+20%|contenido=<math> |
| - | | + | |
| - | <math> | + | |
| E\, | E\, | ||
| - | </math> | + | </math>}}. Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas. |
| - | . Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento | + | *Al conjunto de todos los sucesos que pueden tener lugar en un experimento aleatorio se le llama '''espacio de sucesos''' y se designa por {{sube|porcentaje=+20%|contenido=<math> |
| - | aleatorio utilizaremos letras mayúsculas. | + | |
| - | + | ||
| - | Al conjunto de todos los sucesos que pueden tener lugar en un experimento aleatorio se le llama | + | |
| - | espacio de sucesos y se designa por <math> | + | |
| S\, | S\, | ||
| - | </math> | + | </math>}}. Si {{sube|porcentaje=+20%|contenido=<math> |
| - | . | + | E\, |
| - | + | </math>}} tiene un número finito, <math>n\,</math>, de elementos, el número de sucesos de {{sube|porcentaje=+20%|contenido=<math> | |
| - | Si <math>E\,</math> tiene un número finito, <math>n\,</math>, de elementos, el número de sucesos de <math> | + | |
| E\, | E\, | ||
| - | </math> es <math>2^n\,</math> | + | </math>}} es {{sube|porcentaje=+20%|contenido=<math> |
| + | 2^n\, | ||
| + | </math>}} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Sucesos'' | {{Ejemplo|titulo=Ejemplo: ''Sucesos'' | ||
| |enunciado= | |enunciado= | ||
| - | En el ejemplo anterior, determina los sucesos de <math> | + | En el experimento "lanzar dos dados y anotar la suma de los puntos", determina los siguientes sucesos del espacio muestral: |
| - | E\, | + | |
| - | </math>: | + | |
| - | a)Salir múltiplo de 5. b)Salir número primo. c)Salir mayor o igual que 10. | + | a) Salir múltiplo de 5.{{b4}} b) Salir número primo.{{b4}} c) Salir mayor o igual que 10. |
| |sol= | |sol= | ||
| - | a)Salir múltiplo de 5: | + | a) Salir múltiplo de 5: |
| <math> | <math> | ||
| A = | A = | ||
| Línea 105: | Línea 98: | ||
| <br/> | <br/> | ||
| - | b)Salir número primo: | + | b) Salir número primo: |
| <math> | <math> | ||
| B = | B = | ||
| Línea 116: | Línea 109: | ||
| <br/> | <br/> | ||
| - | c)Salir mayor o igual que 10: | + | c) Salir mayor o igual que 10: |
| <math> | <math> | ||
| C = | C = | ||
| Línea 129: | Línea 122: | ||
| <br/> | <br/> | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | '''Sucesos elementales''' son los que están formados por un solo resultado del | + | *'''Sucesos elementales''' son los que están formados por un solo resultado del |
| experimento. | experimento. | ||
| - | <br/> | + | *'''Sucesos compuestos''' son los que estan formados por dos o más resultados del |
| - | '''Sucesos compuestos''' son los que estan formados por dos o más resultados del | + | |
| experimento; es decir, por dos o más sucesos elementales. | experimento; es decir, por dos o más sucesos elementales. | ||
| - | <br/> | + | *'''Suceso seguro''' es el que se verifica al realizar el experimento aleatorio. Está |
| - | '''Suceso seguro''' es el que se verifica al realizar el experimento aleatorio. Está | + | |
| formado por todos los resultados posibles del experimento y, por tanto, coincide con el | formado por todos los resultados posibles del experimento y, por tanto, coincide con el | ||
| espacio muestral. | espacio muestral. | ||
| - | <br/> | + | *'''Suceso imposible''' es el que nunca se verifica. Se representa por <math> |
| - | '''Suceso imposible''' es el que nunca se verifica. Se representa por | + | |
| - | <math> | + | |
| \emptyset | \emptyset | ||
| - | </math> | + | </math>. |
| - | . | + | |
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Probabilidad]] | [[Categoría: Matemáticas]][[Categoría: Probabilidad]] | ||
Revisión de 10:35 8 jun 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Experimentos y sucesos aleatorios
Un fenómeno o experimento aleatorio es aquel en el que no se puede preveer con certeza el resultado que va tener lugar al observar el fenómeno o al realizar el experimento.
- Al lanzar una moneda al aire, no sabemos si va a salir cara o cruz. Por tanto, se trata de un experimento aleatorio en el que los posibles resultados son "salir cara" o "salir cruz".
- Si nos preguntamos si lloverá mañana, caben dos posibilidades: "si" o "no", y no sabemos con certeza que ocurrirá.
Espacio muestral
Espacio muestral es el conjunto formado por todos los resultados de un experimento o
fenómeno aleatorio. Lo denotamos con la letra 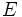 .
.
Ejemplo: Espacio muestral
- ¿Cuál es el espacio muestral asociado al experimento de "lanzar dos dados y anotar la suma de los puntos"?
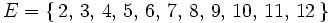
|
Ejercicios: Espacio muestral 1.Describe el espacio muestral asociado a cada uno de los siguientes experimentos aleatorios: a) Lanzar tres monedas. b) Lanzar tres dados y anotar la suma de los puntos obtenidos. c) Extracción de dos bolas de una urna que contiene cuatro bolas blancas y tres negras. d) El tiempo, con relación a la lluvia, que hará durante tres días consecutivos.Solución: a) Llamando C a obtener cara y X a la obtención de cruz, obtenemos el siguiente espacio muestral: E={(CCC),(CCX),(CXC),(XCC),(CXX),(XCX),(XXC),(XXX)} b) E={3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18} c) Llamando B a sacar bola blanca y N a sacar bola negra, tenemos: E={BB,BN,NN} d) Si llamamos L al día lluvioso y N al día sin lluvia, para tres días consecutivos se obtiene el siguiente espacio muestral: E={(LLL),(LLN),(LNL),(NLL),(LNN),(NLN),(NNL),(NNN)} |
Sucesos
- Suceso de un fenómeno aleatorio es cada uno de los subconjuntos del espacio muestral
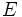 . Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas.
. Para designar cualquier suceso, tambien llamado suceso aleatorio, de un experimento aleatorio utilizaremos letras mayúsculas.
- Al conjunto de todos los sucesos que pueden tener lugar en un experimento aleatorio se le llama espacio de sucesos y se designa por
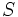 . Si
. Si 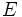 tiene un número finito,
tiene un número finito,  , de elementos, el número de sucesos de
, de elementos, el número de sucesos de 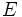 es
es 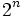
Ejemplo: Sucesos
En el experimento "lanzar dos dados y anotar la suma de los puntos", determina los siguientes sucesos del espacio muestral:
a) Salir múltiplo de 5. b) Salir número primo. c) Salir mayor o igual que 10.
a) Salir múltiplo de 5:
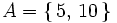
b) Salir número primo:
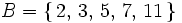
c) Salir mayor o igual que 10:
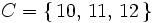
Analicemos los tipos mas frecuentes de sucesos.
- Sucesos elementales son los que están formados por un solo resultado del
experimento.
- Sucesos compuestos son los que estan formados por dos o más resultados del
experimento; es decir, por dos o más sucesos elementales.
- Suceso seguro es el que se verifica al realizar el experimento aleatorio. Está
formado por todos los resultados posibles del experimento y, por tanto, coincide con el espacio muestral.
- Suceso imposible es el que nunca se verifica. Se representa por
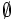 .
.

