Probabilidad de un suceso (3ºESO)
De Wikipedia
| Revisión de 06:51 9 jun 2009 Coordinador (Discusión | contribuciones) (→Probabilidad e un suceso) ← Ir a diferencia anterior |
Revisión de 08:51 9 jun 2009 Coordinador (Discusión | contribuciones) (→Probabilidad e un suceso) Ir a siguiente diferencia → |
||
| Línea 33: | Línea 33: | ||
| }} | }} | ||
| }} | }} | ||
| - | <br> | + | {{p}} |
| + | ==Sucesos equiprobables== | ||
| + | {{Caja_Amarilla|texto=Dos sucesos son '''equiprobables''' si tienen la misma probabilidad de que ocurran al realizar un experimento aleatorio. En caso contrario se dice que son '''no equiprobables'''. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividades Interactivas: ''Sucesos equiprobables y no equiprobables'' | ||
| + | |cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1.''' Sucesos equiprobables''' | ||
| + | |actividad=Aquí tenemos una simulación de un dado tetraédrico. Tiene cuatro caras, y el número que contabilizamos como que ha salido es el de la base. En la escena se supone que hemos lanzado una vez el dado y ha salido el número que se indica. Sigue las siguientes instrucciones y contesta a las preguntas que se te plantean a continuación. | ||
| + | |||
| + | '''Instrucciones:''' | ||
| + | *Fíjate en el número que aparece en la base del tetraedro. Ése es el número que sale cada vez que "lanzamos" el dado. | ||
| + | *A continuación pincha en la flechita azul que acompaña al control del número que se ha obtenido. | ||
| + | *Cada vez que lo hagas se añade el resultado obtenido en la tabla adjunta y se produce otro "lanzamiento". | ||
| + | |||
| + | |||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Azar_y_probabilidad/azar_probabilidad_1a.html | ||
| + | width=100% | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 2.''' Sucesos no equiprobables | ||
| + | |actividad=Va comenzar con una carrera de coches. En las escenas siguientes tenemos el lanzamiento de dos dados y los coches de la carrera. | ||
| + | |||
| + | Los coches de este juego se mueven de la siguiente forma: se lanzan los dos dados, y avanza un casillero, arrastrando con el ratón, el coche cuyo número coincida con la suma de los puntos. | ||
| + | |||
| + | JUEGA y ¡VEREMOS QUIEN GANA! | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Azar_y_probabilidad/azar_probabilidad_1b.html | ||
| + | width=100% | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe>><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Azar_y_probabilidad/azar_probabilidad_1c.html | ||
| + | width=100% | ||
| + | height=400 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | |||
| + | Una vez hayas jugado y anotado cuál ha sido el coche ganador, fíjate en la posición en que han quedado todos los coches. | ||
| + | ¿Crees que todos tenían la misma probabilidad de ganar? | ||
| + | |||
| + | |||
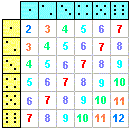
| + | Observa atentamente esta tabla e intenta relacionar con ella el resultado del juego. | ||
| + | [[Imagen:tabladados.gif|center]] | ||
| + | |||
| + | Las sumas de los dos dados NO tienen la misma probabilidad de ocurrir. Se dice que son sucesos que son SUCESOS NO EQUIPROBABLES. | ||
| + | |||
| + | }} | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Probabilidad]] | [[Categoría: Matemáticas]][[Categoría: Probabilidad]] | ||
Revisión de 08:51 9 jun 2009
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Probabilidad e un suceso
Un experimento aleatorio se caracteriza porque repetido muchas veces y en idénticas condiciones el cociente entre el número de veces que ocurre un suceso y el número total de veces que se realiza el experimento tiende a un número fijo, comprendido entre 0 y 1. Esta propiedad es conocida como ley de los grandes números, establecida por Jakob Bernouilli.
Esto nos permite dar la siguiente definición:
Probabilidad de un suceso es el número al que tiende la frecuencia relativa asociada al suceso a medida que aumenta el número de veces que se realiza el experimento.
|
Actividades Interactivas: Probabilidad
Actividad 1. Ley de los grandes números
Actividad: En esta escena veremos lo que ocurre cuando tiramos una moneda muchas veces. Primero tienes que elegir, en la casilla tiutlada "Múltiplos de", que establece de cuánto en cuánto tiramos las monedas (de 10 en 10, de 100 en 100, etc.). A continuación, pulsando sobre la flecha azul del control "Tiradas", simularemos el lanzamiento de monedas en la cantidad deseada. En cada caso obtendremos la frecuencia relativa de cada suceso, y una gráfica con el número de caras. Prueba con diferentes tiradas y observa el resultado de las frecuencias relativas en cada caso |
Sucesos equiprobables
Dos sucesos son equiprobables si tienen la misma probabilidad de que ocurran al realizar un experimento aleatorio. En caso contrario se dice que son no equiprobables.
|
Actividades Interactivas: Sucesos equiprobables y no equiprobables
Actividad 1. Sucesos equiprobables
Actividad: Aquí tenemos una simulación de un dado tetraédrico. Tiene cuatro caras, y el número que contabilizamos como que ha salido es el de la base. En la escena se supone que hemos lanzado una vez el dado y ha salido el número que se indica. Sigue las siguientes instrucciones y contesta a las preguntas que se te plantean a continuación. Instrucciones:
Actividad 2. Sucesos no equiprobables
Actividad: Va comenzar con una carrera de coches. En las escenas siguientes tenemos el lanzamiento de dos dados y los coches de la carrera. Los coches de este juego se mueven de la siguiente forma: se lanzan los dos dados, y avanza un casillero, arrastrando con el ratón, el coche cuyo número coincida con la suma de los puntos. JUEGA y ¡VEREMOS QUIEN GANA! >
|