Funciones lineales: Calculadora
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:12 7 ago 2007 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| + | {{Menú Matemáticas 3ESO | ||
| + | |ir= |ampliar=[http://averroes.ced.junta-andalucia.es/iesarroyo/matematicas/materiales/3eso/solucionlibro/unidad11.pdf Ejercicios]<br>[http://mimosa.cnice.mecd.es/clobo/geoweb/geoana4.htm Ecuación pto-pendiente]<br>[http://www.ematematicas.net/ecrectaplano.php?a=5 Ecuaciones de la recta]<br> | ||
| + | [http://www.ematematicas.net/posicionrelativa.php?a=5 Posición relativa] | ||
| + | |repasar= | ||
| + | [http://descartes.cnice.mecd.es/1y2_eso/Funciones_funcion_de_proporcionalidad/index.htm Proporcionalidad directa] | ||
| + | |enlaces=[http://es.wikipedia.org/wiki/Funci%C3%B3n_lineal Función lineal]<br>[http://es.wikipedia.org/wiki/Recta Recta] | ||
| + | }} | ||
| + | {{p}} | ||
| ==Calculadora== | ==Calculadora== | ||
| {{Wiris | {{Wiris | ||
| Línea 8: | Línea 16: | ||
| |contenido= | |contenido= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/wikipedia/wiris/rectas.html | + | url=http://maralboran.org/wikipedia/wiris/rectas.html |
| width=100% | width=100% | ||
| height=400 | height=400 | ||
Revisión actual
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Proporcionalidad directa | Ejercicios Ecuación pto-pendiente Ecuaciones de la recta | WIRIS Geogebra Calculadora Función lineal Recta |
[editar]
Calculadora
WIRIS: Ecuación de la recta
Revisa estos ejemplos:
Ejemplos:
y utiliza el editor para contestar las siguientes preguntas:
- a) Halla la ecuación de la recta que pasa por los puntos (-2,4) y (5,6). Halla su pendiente.
- b) Halla la ecuación de la recta que pasa por el punto (-1,2) y tiene pendiente 5.
- c) Hallar el punto de corte de las rectas
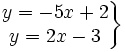 graficamente y resolviendo el sistema.
graficamente y resolviendo el sistema.
- d) Dibuja dos rectas paralelas y observa el valor de sus pendientes. ¿Cómo son?

