Medida de la correlación (1ºBach)
De Wikipedia
| Revisión de 17:21 22 oct 2014 Coordinador (Discusión | contribuciones) (→Propiedades del coeficiente de correlación) ← Ir a diferencia anterior |
Revisión de 17:29 22 oct 2014 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 47: | Línea 47: | ||
| {{Casio FX-100MS Regresion Lineal}} | {{Casio FX-100MS Regresion Lineal}} | ||
| - | [[Categoría: Matemáticas]] | + | [[Categoría: Matemáticas]][[Categoría: Estadística|Bidimensional]] |
Revisión de 17:29 22 oct 2014
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
En el apartado anterior hemos visto de manera intuitiva como puede ser la correlación ente dos variables dependiendo del agrupamiento de los puntos de la nube en torno a una recta. Ahora vamos a ver cómo se puede cuantificar dicha correlación mediante un parámetro que denominaremos coeficiente de correlación.
Consideremos una distribución bidimensional de cuyas variables 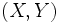 tenemos
tenemos 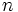 valores observados:
valores observados:
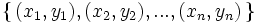
Centro de gravedad de una distribución bidimensional
Llamaremos centro de gravedad de la distribución al punto 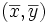 cuyas coordenadas son las medias de las distribuciones unidimensionales de X e Y:
cuyas coordenadas son las medias de las distribuciones unidimensionales de X e Y:
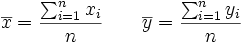
Covarianza
Se llama covarianza de la distribución al parámetro:
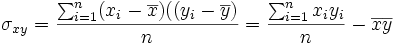
Coeficiente de correlación
Llamaremos coeficiente de correlación entre las dos variables al parámetro:
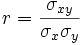
donde σxy es la covarianza y σx,σy son las desviaciones típicas de las distribuciones unidimensionales de X e Y:
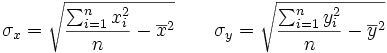
Propiedades del coeficiente de correlación
El coeficiente de correlación tiene las siguientes propiedades:
- No tiene dimensiones, es decir, no depende de las unidades en las que vengan dadas las variables.
- Está comprendido entre -1 y 1:
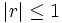
- Cuanto más fuerte sea la correlación más próximo a 1 estará
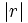 y cuanto más débil sea la correlación más próximo a 0 estará
y cuanto más débil sea la correlación más próximo a 0 estará 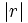 .
.
- Si
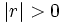 la correlación será positiva y si
la correlación será positiva y si 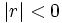 la correlación será negativa.
la correlación será negativa.
Calculadora
|
Calculadora: Modo Regresión Lineal (REG / Lin) Para calcular los parámetros de distribuciones bidimensionales primero deberemos establecer en la calculadora el modo "Regresión Lineal" mediante la secuencia de teclas: |
|
Calculadora: Modo básico (COMP) Cuando se desea retornar la calculadora al modo "básico" tras haber trabajado en otro modo (p.e. el modo "Regresión Lineal") deberemos teclear la secuencia: |
|
Calculadora: Borrado de la memoria estadística (SCL: Statistical Clear) Para trabajar con variables estadísticas bidimensionales primero deberemos borrar los posibles datos estadísticos que hubiese en memoria mediante la secuencia de teclas: |

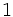
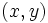 correspondientes a los datos de una variable bidimensional, introduciremos primero el valor
correspondientes a los datos de una variable bidimensional, introduciremos primero el valor 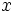 seguido de la tecla
seguido de la tecla 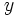 y terminando con la tecla
y terminando con la tecla  de veces, después del valor
de veces, después del valor 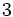
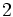
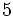
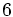
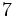
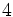
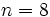 , que es el número de datos introducidos. Si cometemos algún error, podemos movernos hacia arriba o hacia abajo con la tecla de movimiento del cursor, que es la tecla grande central, y corregir los datos erroneos. Tras corregir cada dato deberemos pulsar la tecla
, que es el número de datos introducidos. Si cometemos algún error, podemos movernos hacia arriba o hacia abajo con la tecla de movimiento del cursor, que es la tecla grande central, y corregir los datos erroneos. Tras corregir cada dato deberemos pulsar la tecla 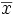 (media de la variable unidimensional X) teclearemos
(media de la variable unidimensional X) teclearemos 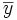 (media de la variable unidimensional Y) teclearemos
(media de la variable unidimensional Y) teclearemos 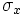 (desviación típica de la variable unidimensional X) teclearemos
(desviación típica de la variable unidimensional X) teclearemos 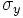 (desviación típica de la variable unidimensional Y) teclearemos
(desviación típica de la variable unidimensional Y) teclearemos 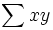 (suma de los productos) teclearemos
(suma de los productos) teclearemos  (coeficiente de correlación) teclearemos
(coeficiente de correlación) teclearemos 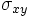 no se puede obtener directamente de la calculadora, hay que obtenerla a partir de la fórmula
no se puede obtener directamente de la calculadora, hay que obtenerla a partir de la fórmula