Plantilla:Valor absoluto (1º Bach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:26 16 ago 2016 Coordinador (Discusión | contribuciones) (→Valor absoluto de un número real) ← Ir a diferencia anterior |
Revisión de 10:05 29 ago 2016 Coordinador (Discusión | contribuciones) (→Ejemplos) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| ::'''2)''' ¿Para qué valores de x se cumplen las siguientes expresiones? | ::'''2)''' ¿Para qué valores de x se cumplen las siguientes expresiones? | ||
| :::a) <math>|x|=3\;</math> | :::a) <math>|x|=3\;</math> | ||
| + | |||
| :::b) <math>|x|=0\;</math> | :::b) <math>|x|=0\;</math> | ||
| + | |||
| :::c) <math>|x|=\sqrt{3}\;</math> | :::c) <math>|x|=\sqrt{3}\;</math> | ||
| ::'''3)''' ¿Para qué valores de x se cumplen las siguientes desigualdades? | ::'''3)''' ¿Para qué valores de x se cumplen las siguientes desigualdades? | ||
| :::b) <math>|x|<3\;</math> | :::b) <math>|x|<3\;</math> | ||
| + | |||
| :::b) <math>|x| \ge 3\;</math> | :::b) <math>|x| \ge 3\;</math> | ||
| + | |||
| :::c) <math>|x-2|\le 3\;</math> | :::c) <math>|x-2|\le 3\;</math> | ||
| Línea 55: | Línea 59: | ||
| : Resuelve | : Resuelve | ||
| ::a) <math>|3x-1|=0 \;</math> | ::a) <math>|3x-1|=0 \;</math> | ||
| + | |||
| ::b) <math>|3x-1|=4 \;</math> | ::b) <math>|3x-1|=4 \;</math> | ||
| + | |||
| ::c) <math>|x-5|>2 \;</math> | ::c) <math>|x-5|>2 \;</math> | ||
Revisión de 10:05 29 ago 2016
Tabla de contenidos |
Valor absoluto de un número real
(pág. 30)
El valor absoluto o módulo de un número real  es el propio número
es el propio número  , si es positivo, o su opuesto,
, si es positivo, o su opuesto, 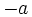 , si es negativo. Es decir:
, si es negativo. Es decir:
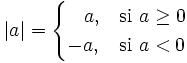
Nótese que el valor absoluto de un número siempre será positivo. Desde un punto de vista geométrico, el valor absoluto de un número real  corresponde a la distancia a lo largo de la recta real desde
corresponde a la distancia a lo largo de la recta real desde  hasta el cero.
hasta el cero.
Como consecuencia, en una inecuación:
- Lo que está sumando en un lado de la desigualdad, pasa restando al otro miembro sin afectar a la desigualdad. Y viceversa.
- Lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa. En este caso la desigualdad sólo cambia de sentido si el número que pasa multiplicando o dividiendo es negativo.
¿Cuándo debe cambiar de sentido una desigualdad?. Ejemplos.
Ejemplos
(pág. 30)
Ejercicios resueltos: Valor absoluto
- 1) Calcula el valor absoluto de los siguientes números:
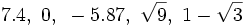
- 1) Calcula el valor absoluto de los siguientes números:
- 2) ¿Para qué valores de x se cumplen las siguientes expresiones?
- a)
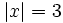
- a)
- 2) ¿Para qué valores de x se cumplen las siguientes expresiones?
- b)
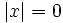
- b)
- c)
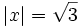
- c)
- 3) ¿Para qué valores de x se cumplen las siguientes desigualdades?
- b)
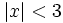
- b)
- 3) ¿Para qué valores de x se cumplen las siguientes desigualdades?
- b)
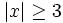
- b)
- c)
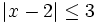
- c)
Solución:
1)
2)
- a)
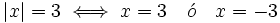
- b)
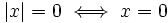
- c)
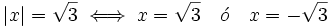
3)
- a)

- b)
![|x| \ge 3 \iff x \le-3 \quad \acute{o} \quad x \ge 3 \iff x \in \left ( -\infty , -3 \right ] \cup \left [ 3, +\infty \right ) \iff x \in \mathbb{R}-\left ( -3, 3 \right )](/wikipedia/images/math/b/4/9/b49b95a7c4bd7c4ee4a2c954f8c3c0a8.png)
- c)
![|x-2|\le 3 \iff -3<x-2<3 \iff -3+2<x-2+2<3+2 \iff -1<x<5 \iff x \in \left [ -1 , 5 \right ]](/wikipedia/images/math/5/7/b/57bf2f22393d95f6eaa7bf5ac35e5422.png)
|
Actividad: Valor absoluto
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Videotutoriales
- Definición del valor absoluto de un número.
- Ejemplos.
- Propiedades del valor absoluto.
- Definición de distancia entre dos puntos de la recta real:
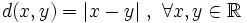
- Ejemplos.
Ejercicios
(pág. 30)
|
Ejercicios propuestos: Valor absoluto |
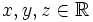 , se cumplen las siguientes propiedades:
, se cumplen las siguientes propiedades:
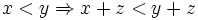
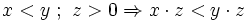
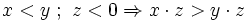
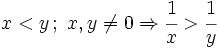
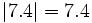
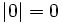
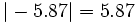
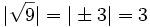
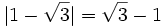
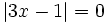
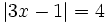
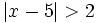
 b)
b)  c)
c) 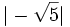
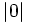 e)
e)  f)
f) 
 h)
h)  i)
i) 
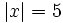 b)
b) 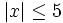 c)
c) 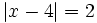
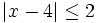 e)
e) 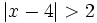 f)
f)