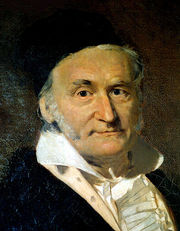Gauss
De Wikipedia
| Revisión de 18:06 28 dic 2008 Coordinador (Discusión | contribuciones) (→Vida) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 9: | Línea 9: | ||
| Como su padre quería que seguiera sus mismos pasos y se convertiera en albañil, no apoyó la educación de Gauss en matemáticas y ciencias. Gauss recibió apoyo de su madre y del duque de Braunschweig, quien concedió a Gauss una beca para el Colegio Carolinum (ahora Technische Universität Braunschweig), al que asistió entre 1792 y 1795, y posteriormente se trasladó a la Universidad de Göttingen de 1795 a 1798. En la universidad, Gauss redescubrió varios teoremas importantes de forma independiente. | Como su padre quería que seguiera sus mismos pasos y se convertiera en albañil, no apoyó la educación de Gauss en matemáticas y ciencias. Gauss recibió apoyo de su madre y del duque de Braunschweig, quien concedió a Gauss una beca para el Colegio Carolinum (ahora Technische Universität Braunschweig), al que asistió entre 1792 y 1795, y posteriormente se trasladó a la Universidad de Göttingen de 1795 a 1798. En la universidad, Gauss redescubrió varios teoremas importantes de forma independiente. | ||
| + | [[Image:Therese Gauss.jpg|right|thumb|Therese, hija de Gauss (1816 - 1864)]] | ||
| + | La vida personal de Gauss se vio empañada por la temprana muerte de su primera esposa, Johanna Osthoff, en 1809, seguida de la muerte de un hijo, Louis. Gauss se sumió en una depresión a partir de la cual nunca se recuperó plenamente. Se casó de nuevo, con la mejor amiga de Johanna, Friederica Wilhelmine Waldeck, familiarmente conocida como Minna. Cuando su segunda esposa murió en 1831, después de una larga enfermedad, una de sus hijas, Therese, se hizo cargo del hogar y del cuidado de Gauss hasta el final de su vida. Su madre vivió en su casa desde 1817 hasta su muerte en 1839. Tuvo en total seis hijos, tres con cada una de sus esposas. Gauss tuvo algunos conflictos con sus hijos y, como consecuencia, dos de ellos emigraron a los Estados Unidos. | ||
| Gauss fue un prodigio del cálculo mental. Cuando se le preguntó cómo había sido capaz de predecir con tal precisión la trayectoria de Ceres en 1801, él respondió, "Usando logaritmos". El entrevistador entonces quiso saber cómo había sido capaz de buscar tantos números en las tablas con tanta rapidez. "Buscarlos?" respondió Gauss. "¿Quién tuvo que buscarlos? Los calculé de cabeza!" | Gauss fue un prodigio del cálculo mental. Cuando se le preguntó cómo había sido capaz de predecir con tal precisión la trayectoria de Ceres en 1801, él respondió, "Usando logaritmos". El entrevistador entonces quiso saber cómo había sido capaz de buscar tantos números en las tablas con tanta rapidez. "Buscarlos?" respondió Gauss. "¿Quién tuvo que buscarlos? Los calculé de cabeza!" | ||
| + | [[Imagen:tumbagauss.jpg|thumb|right|150 px| Tumba de Gauss en Göttingen]] | ||
| En 1809 fue nombrado director del Observatorio de Göttingen. | En 1809 fue nombrado director del Observatorio de Göttingen. | ||
| + | |||
| + | Gauss era un perfeccionista y un duro trabajador. Según Isaac Asimov, Gauss fue interrumpido en medio de un problema para decirle que su mujer se estaba muriendo. Presuntamente el dijo, "Dile que espere un momento hasta que haya terminado." Esta anécdota se sugiere que se trata de una historia apócrifa. | ||
| + | |||
| + | Nunca fue un prolífico escritor, al negarse a publicar obras que no consideraba completas y libres de crítica. Esto está en consonancia con su lema personal ''pauca sed matura'' ( "pocos, pero maduros"). Sus diarios personales indican que él había hecho importantes descubrimientos matemáticos años o décadas antes que sus contemporáneos los publicasen. El historiador de matemáticas Eric Templo Bell, estima que si Gauss hubiese publicado a tiempo todos sus descubrimientos, las matemáticas habrían avanzado cincuenta años. | ||
| + | |||
| + | Aunque a Gauss le desagradaba dar clases, algunos de sus alumnos resultaron destacados matemáticos como [[Dedekind|Richard Dedekind]], [[Riemann|Bernhard Riemann]]y Friedrich Bessel. Antes de morir, Sophie Germain fue recomendada por Gauss para recibir el título de Doctor Honoris Causa. | ||
| + | |||
| + | Se dice que asistió a una sola conferencia científica, que fue en Berlín en 1828. | ||
| + | |||
| Gauss murió en Göttingen, Hannover (ahora parte de la Baja Sajonia, Alemania) el 23 de febrero de 1855 y está enterrado en el cementerio Albanifriedhof. Dos personas lo elogiaron en su funeral, su yerno Wolfgang Ewald y Heinrich von Waltershausen Sartorius, que era amigo cercano de Gauss y su biógrafo. Su cerebro fue conservado y fue estudiado por Rudolf Wagner. Este calculo el peso (1492 gramos) y el área cerebral (219588 milímetros cuadrados). Se observaron convoluciones altamente desarolladas, lo que a principios del siglo XX fue considerado como una explicación de su genio. | Gauss murió en Göttingen, Hannover (ahora parte de la Baja Sajonia, Alemania) el 23 de febrero de 1855 y está enterrado en el cementerio Albanifriedhof. Dos personas lo elogiaron en su funeral, su yerno Wolfgang Ewald y Heinrich von Waltershausen Sartorius, que era amigo cercano de Gauss y su biógrafo. Su cerebro fue conservado y fue estudiado por Rudolf Wagner. Este calculo el peso (1492 gramos) y el área cerebral (219588 milímetros cuadrados). Se observaron convoluciones altamente desarolladas, lo que a principios del siglo XX fue considerado como una explicación de su genio. | ||
| - | [[Imagen:tumbagauss.jpg|thumb|right|150 px| Tumba de Gauss en Göttingen]] | ||
| ==Obra== | ==Obra== | ||
| Línea 36: | Línea 47: | ||
| Fue el primero en probar rigurosamente el [[Teorema Fundamental del Álgebra]] (disertación para su tesis doctoral en 1799), aunque una prueba casi completa de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente. | Fue el primero en probar rigurosamente el [[Teorema Fundamental del Álgebra]] (disertación para su tesis doctoral en 1799), aunque una prueba casi completa de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente. | ||
| - | En 1801 publicó el libro ''Disquisitiones Aritmeticae'', con seis secciones dedicadas a la Teoría de números, dándole a esta rama de las matemáticas una estructura sistematizada. En la última sección del libro expone su tesis doctoral. Ese mismo año predijo la órbita del asteroide Cere aproximando parámetros por mínimos cuadrados. | + | En 1801 publicó el libro ''Disquisitiones Aritmeticae'', con seis secciones dedicadas a la Teoría de números, dándole a esta rama de las matemáticas una estructura sistematizada. En la última sección del libro expone su tesis doctoral. Ese mismo año predijo la órbita del asteroide Cere aproximando parámetros por el método de mínimos cuadrados, un procedimiento utilizado en todas las ciencias hasta el día de hoy para minimizar los efectos del error de medición. |
| === Madurez === | === Madurez === | ||
| Línea 48: | Línea 59: | ||
| Mostró un gran interés en geometría diferencial y su trabajo ''Disquisitiones generales circa superficies curva'' publicado en 1828 fue el más reconocido en este campo. En dicha obra expone el famoso '''teorema egregium'''. De esta obra se deriva el término curvatura gaussiana. | Mostró un gran interés en geometría diferencial y su trabajo ''Disquisitiones generales circa superficies curva'' publicado en 1828 fue el más reconocido en este campo. En dicha obra expone el famoso '''teorema egregium'''. De esta obra se deriva el término curvatura gaussiana. | ||
| - | En 1831 se asocia al físico Wilhelm Weber durante seis fructíferos años en los que realizan investigaciones sobre las Leyes de Kirchhoff, publicaciones sobre magnetismo y construyen un telégrafo eléctrico primitivo. | + | En 1831 se asocia al físico Wilhelm Weber durante seis fructíferos años en los que realizan investigaciones sobre las Leyes de Kirchhoff, publicaciones sobre magnetismo y construyen un telégrafo eléctrico primitivo. |
| + | |||
| + | ==Conmemoraciones== | ||
| + | [[Image:10 DM Serie4 Vorderseite.jpg|thumb|Billete de 10 marcos alemán (1993) mostrando a Gauss]] | ||
| + | [[Image:Stamp Carl Friedrich Gauss.jpg|thumb|Gauss en un sello de Alemania Oriental (1977)]] | ||
| + | |||
| + | *Desde 1989 hasta finales de 2001, su retrato y una curva de distribución normal, así como algunos edificios destacados de Göttingen fueron representados en los billetes de 10 marcos alemanes. | ||
| + | *Alemania también emitió tres sellos en honor de Gauss. Uno de ellos, se publicó en 1955, en el centenario de su muerte; otros dos, se publicaron en 1977, en el 200 aniversario de su nacimiento. | ||
| + | *En 2007, su busto se incorporó a la colección del templo Walhalla. | ||
| - | Aunque a Gauss le desagradaba dar clases, algunos de sus alumnos resultaron destacados matemáticos como [[Richard Dedekind]] y [[Bernhard Riemann]]. Otros matemáticos contemporáneos fueron [[Carl Gustav Jakob Jacobi]], [[Dirichlet]] y [[Sophie Germain]]. | + | ===Cosas nombradas en honor a Gauss=== |
| + | *La unidad de inducción magnética, el Gauss. | ||
| + | *El crater Gauss de la Luna | ||
| + | *El asteroide 1001 Gaussia. | ||
| + | *El buque Gauss, utilizado en expedición de Gauss a la Antártida. | ||
| + | *Gaussberg, un volcán extinto descubierto por la anterior expedición. | ||
| + | *La Torre Gauss, una torre de observación en Dransfeld, Alemania. | ||
| + | *En las escuelas secundarias de Canadá, una competición anual de la competencia matemática nacional administrada por el Centro de Enseñanza de las Matemáticas y Computación tiene su nombre en honor a Gauss. | ||
| + | *En la Universidad de California, Santa Cruz, en el Colegio Corona, la construcción de un dormitorio lleva el nombre de Gauss. | ||
| + | *El Gauss Haus, un centro de resonancia magnética nuclear de la Universidad de Utah. | ||
| + | *La escuela Carl-Friedrich-Gauss de Matemáticas, Ciencias de la Computación, Administración de Empresas, Economía y Ciencias Sociales de la Universidad de Braunschweig. | ||
| ==Video== | ==Video== | ||
| - | {{Video2b | + | {{Video_enlace |
| - | |titulo1=Gauss, el príncipe de las matemáticas | + | |titulo1=Gauss, de lo real a lo imaginario |
| |duracion=22´ | |duracion=22´ | ||
| |sinopsis=Principios del siglo XIX. Un joven matemático acaba de resolver un problema de más de 2.000 años de antigüedad: la construcción con regla y compás del polígono regular de 17 lados. Esta va a ser una de las primeras anotaciones que hará en una vieja libreta de 19 páginas. Al final de su vida las anotaciones no llegarán a 50, pero sin duda esta libreta será el sueño de cualquier matemático del siglo XIX. Las aportaciones que en ella se reflejan contienen el suficiente material para mantener ocupados a todos los matemáticos del siglo. | |sinopsis=Principios del siglo XIX. Un joven matemático acaba de resolver un problema de más de 2.000 años de antigüedad: la construcción con regla y compás del polígono regular de 17 lados. Esta va a ser una de las primeras anotaciones que hará en una vieja libreta de 19 páginas. Al final de su vida las anotaciones no llegarán a 50, pero sin duda esta libreta será el sueño de cualquier matemático del siglo XIX. Las aportaciones que en ella se reflejan contienen el suficiente material para mantener ocupados a todos los matemáticos del siglo. | ||
| Línea 61: | Línea 90: | ||
| Las increíbles aportaciones de Gauss no se limitan al mundo de las Matemáticas y de la Astronomía. Junto a Weber va a poner en marcha el primer telégrafo operativo unos años antes que el de Morse. En magnetismo también nos ha dejado su huella: el primer mapa magnético de la Tierra es obra suya. No es inmerecido el título de Príncipe de los Matemáticos, aunque reinó en casi todas las ciencias. | Las increíbles aportaciones de Gauss no se limitan al mundo de las Matemáticas y de la Astronomía. Junto a Weber va a poner en marcha el primer telégrafo operativo unos años antes que el de Morse. En magnetismo también nos ha dejado su huella: el primer mapa magnético de la Tierra es obra suya. No es inmerecido el título de Príncipe de los Matemáticos, aunque reinó en casi todas las ciencias. | ||
| - | |url1=http://maralboran.org/web_ma/videos/gauss/gauss.htm | + | |url1=http://www.rtve.es/alacarta/videos/universo-matematico/paterna-universo-matematico-20100923-1907/1201226/ |
| + | |url2=http://maralboran.org/web_ma/videos/gauss/gauss.htm | ||
| + | |url3=http://c0/helvia/aula/archivos/repositorio//0/102/html/index.htm | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]] | [[Categoría: Matemáticas]][[Categoría: Historia de las Matemáticas]][[Categoría: Matemáticos]] | ||
Revisión actual
Johann Carl Friedrich Gauss (1777 – 1855), matemático, astrónomo y físico alemán. Contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la geodesia, el magnetismo y la óptica. Considerado "el príncipe de las matemáticas" y "el matemático más grande desde la antigüedad", Gauss ha tenido una influencia notable en muchos campos de la matemática y de la ciencia, y es considerado uno de los matemáticos que más influencia ha tenido en la historia. Fue de los primeros en extender el concepto de divisibilidad a otros conjuntos.
Gauss fue un niño prodigio de quien existen muchas anécdotas acerca de su asombrosa precocidad siendo apenas un infante, e hizo sus primeros grandes descubrimientos mientras era apenas un adolescente. Completó su magnum opus, Disquisitiones Arithmeticae a los veintiún años (1798), aunque no sería publicado hasta 1801. Un trabajo que fue fundamental para que la teoría de los números se consolidara y ha moldeado esta área hasta los días presentes.
Tabla de contenidos |
Vida
Nació el 30 de abril de 1777, en Braunschweig, en el electorado de Brunswick-Lüneburg, que ahora forma parte de la Baja Sajonia, Alemania. Hijo único, de padres de clase trabajadora. Fue bautizado y confirmado en una iglesia cerca de la escuela a la que había asistido de niño. Hay varias historias de su genio precoz. Según una, a la edad de tres años ya dió muestras de sus dones al corregir mentalmente y fallos de cálculo, un error que su padre había cometido en unos cálculos financieros.
Como su padre quería que seguiera sus mismos pasos y se convertiera en albañil, no apoyó la educación de Gauss en matemáticas y ciencias. Gauss recibió apoyo de su madre y del duque de Braunschweig, quien concedió a Gauss una beca para el Colegio Carolinum (ahora Technische Universität Braunschweig), al que asistió entre 1792 y 1795, y posteriormente se trasladó a la Universidad de Göttingen de 1795 a 1798. En la universidad, Gauss redescubrió varios teoremas importantes de forma independiente.
La vida personal de Gauss se vio empañada por la temprana muerte de su primera esposa, Johanna Osthoff, en 1809, seguida de la muerte de un hijo, Louis. Gauss se sumió en una depresión a partir de la cual nunca se recuperó plenamente. Se casó de nuevo, con la mejor amiga de Johanna, Friederica Wilhelmine Waldeck, familiarmente conocida como Minna. Cuando su segunda esposa murió en 1831, después de una larga enfermedad, una de sus hijas, Therese, se hizo cargo del hogar y del cuidado de Gauss hasta el final de su vida. Su madre vivió en su casa desde 1817 hasta su muerte en 1839. Tuvo en total seis hijos, tres con cada una de sus esposas. Gauss tuvo algunos conflictos con sus hijos y, como consecuencia, dos de ellos emigraron a los Estados Unidos.
Gauss fue un prodigio del cálculo mental. Cuando se le preguntó cómo había sido capaz de predecir con tal precisión la trayectoria de Ceres en 1801, él respondió, "Usando logaritmos". El entrevistador entonces quiso saber cómo había sido capaz de buscar tantos números en las tablas con tanta rapidez. "Buscarlos?" respondió Gauss. "¿Quién tuvo que buscarlos? Los calculé de cabeza!"
En 1809 fue nombrado director del Observatorio de Göttingen.
Gauss era un perfeccionista y un duro trabajador. Según Isaac Asimov, Gauss fue interrumpido en medio de un problema para decirle que su mujer se estaba muriendo. Presuntamente el dijo, "Dile que espere un momento hasta que haya terminado." Esta anécdota se sugiere que se trata de una historia apócrifa.
Nunca fue un prolífico escritor, al negarse a publicar obras que no consideraba completas y libres de crítica. Esto está en consonancia con su lema personal pauca sed matura ( "pocos, pero maduros"). Sus diarios personales indican que él había hecho importantes descubrimientos matemáticos años o décadas antes que sus contemporáneos los publicasen. El historiador de matemáticas Eric Templo Bell, estima que si Gauss hubiese publicado a tiempo todos sus descubrimientos, las matemáticas habrían avanzado cincuenta años.
Aunque a Gauss le desagradaba dar clases, algunos de sus alumnos resultaron destacados matemáticos como Richard Dedekind, Bernhard Riemanny Friedrich Bessel. Antes de morir, Sophie Germain fue recomendada por Gauss para recibir el título de Doctor Honoris Causa.
Se dice que asistió a una sola conferencia científica, que fue en Berlín en 1828.
Gauss murió en Göttingen, Hannover (ahora parte de la Baja Sajonia, Alemania) el 23 de febrero de 1855 y está enterrado en el cementerio Albanifriedhof. Dos personas lo elogiaron en su funeral, su yerno Wolfgang Ewald y Heinrich von Waltershausen Sartorius, que era amigo cercano de Gauss y su biógrafo. Su cerebro fue conservado y fue estudiado por Rudolf Wagner. Este calculo el peso (1492 gramos) y el área cerebral (219588 milímetros cuadrados). Se observaron convoluciones altamente desarolladas, lo que a principios del siglo XX fue considerado como una explicación de su genio.
Obra
Infancia
Es célebre la siguiente anécdota: Tenía Gauss diez años cuando un día en la escuela el profesor manda sumar los cien primeros números naturales. El maestro quería unos minutos de tranquilidad... pero transcurridos pocos segundos Gauss levanta la mano y dice tener la solución: los cien primeros números naturales suman 5.050. Y efectivamente es así. ¿Cómo lo hizo Gauss? Pues mentalmente se dio cuenta de que la suma del primer término con el último, la del segundo con el penúltimo, y así sucesivamente, era constante:
Con los 100 números se pueden formar 50 pares, de forma que la solución final viene dada por el producto
Gauss había deducido la fórmula que da la suma de n términos de una progresión aritmética de la que se conocen el primero y el último término:
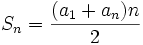
dónde a1 es el primer término, an el último, y n es el número de términos de la progresión.
Juventud
Fue el primero en probar rigurosamente el Teorema Fundamental del Álgebra (disertación para su tesis doctoral en 1799), aunque una prueba casi completa de dicho teorema fue hecha por Jean Le Rond d'Alembert anteriormente.
En 1801 publicó el libro Disquisitiones Aritmeticae, con seis secciones dedicadas a la Teoría de números, dándole a esta rama de las matemáticas una estructura sistematizada. En la última sección del libro expone su tesis doctoral. Ese mismo año predijo la órbita del asteroide Cere aproximando parámetros por el método de mínimos cuadrados, un procedimiento utilizado en todas las ciencias hasta el día de hoy para minimizar los efectos del error de medición.
Madurez
En 1809 publicó Theoria motus corporum coelestium in sectionibus conicis Solem ambientium describiendo cómo calcular la órbita de un planeta y cómo refinarla posteriormente. Profundizó sobre ecuaciones diferenciales y secciones cónicas.
Quizás Gauss haya sido la primera persona en intuir la independencia del postulado de las paralelas de Euclides y de esta manera anticipar una geometría no euclidiana. Pero esto sólo se afirma, sacando conclusiones de cartas enviadas a sus amigos, Farkas Bolyai y a János Bolyai a quien Gauss calificó como un genio de primer orden.
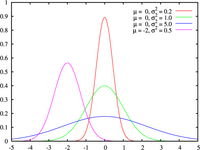
En 1823 publica Theoria combinationis observationum erroribus minimis obnoxiae, dedicado a la estadística, concretamente a la distribución normal cuya curva característica, denominada como Campana de Gauss, es muy usada en disciplinas no matemáticas donde los datos son susceptibles de estar afectados por errores sistemáticos y casuales como por ejemplo la psicología diferencial. Hay que aclarar que Gauss no fue el primero en hacer referencia a la distribución normal.
Mostró un gran interés en geometría diferencial y su trabajo Disquisitiones generales circa superficies curva publicado en 1828 fue el más reconocido en este campo. En dicha obra expone el famoso teorema egregium. De esta obra se deriva el término curvatura gaussiana.
En 1831 se asocia al físico Wilhelm Weber durante seis fructíferos años en los que realizan investigaciones sobre las Leyes de Kirchhoff, publicaciones sobre magnetismo y construyen un telégrafo eléctrico primitivo.
Conmemoraciones
- Desde 1989 hasta finales de 2001, su retrato y una curva de distribución normal, así como algunos edificios destacados de Göttingen fueron representados en los billetes de 10 marcos alemanes.
- Alemania también emitió tres sellos en honor de Gauss. Uno de ellos, se publicó en 1955, en el centenario de su muerte; otros dos, se publicaron en 1977, en el 200 aniversario de su nacimiento.
- En 2007, su busto se incorporó a la colección del templo Walhalla.
Cosas nombradas en honor a Gauss
- La unidad de inducción magnética, el Gauss.
- El crater Gauss de la Luna
- El asteroide 1001 Gaussia.
- El buque Gauss, utilizado en expedición de Gauss a la Antártida.
- Gaussberg, un volcán extinto descubierto por la anterior expedición.
- La Torre Gauss, una torre de observación en Dransfeld, Alemania.
- En las escuelas secundarias de Canadá, una competición anual de la competencia matemática nacional administrada por el Centro de Enseñanza de las Matemáticas y Computación tiene su nombre en honor a Gauss.
- En la Universidad de California, Santa Cruz, en el Colegio Corona, la construcción de un dormitorio lleva el nombre de Gauss.
- El Gauss Haus, un centro de resonancia magnética nuclear de la Universidad de Utah.
- La escuela Carl-Friedrich-Gauss de Matemáticas, Ciencias de la Computación, Administración de Empresas, Economía y Ciencias Sociales de la Universidad de Braunschweig.
Video
Principios del siglo XIX. Un joven matemático acaba de resolver un problema de más de 2.000 años de antigüedad: la construcción con regla y compás del polígono regular de 17 lados. Esta va a ser una de las primeras anotaciones que hará en una vieja libreta de 19 páginas. Al final de su vida las anotaciones no llegarán a 50, pero sin duda esta libreta será el sueño de cualquier matemático del siglo XIX. Las aportaciones que en ella se reflejan contienen el suficiente material para mantener ocupados a todos los matemáticos del siglo.
Sin embargo la fama de este joven, Gauss le va a venir de los cielos. A finales de 1800 los astrónomos descubren un nuevo objeto celeste. No se trata de un cometa, bien podía ser el planeta buscado tantos años entre Marte y Júpiter. Por desgracia se le pierde la pista. Pero con las pocas observaciones realizadas, Gauss se pone a la tarea de deducir su órbita y señala el lugar del cielo hacia donde apuntar los telescopios un año más tarde. Y en efecto alli aparece Ceres.
Las increíbles aportaciones de Gauss no se limitan al mundo de las Matemáticas y de la Astronomía. Junto a Weber va a poner en marcha el primer telégrafo operativo unos años antes que el de Morse. En magnetismo también nos ha dejado su huella: el primer mapa magnético de la Tierra es obra suya. No es inmerecido el título de Príncipe de los Matemáticos, aunque reinó en casi todas las ciencias.