Fórmula del binomio de Newton (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:57 4 sep 2016 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) ← Ir a diferencia anterior |
Revisión de 19:01 4 sep 2016 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) Ir a siguiente diferencia → |
||
| Línea 25: | Línea 25: | ||
| {{p}} | {{p}} | ||
| ===Triángulo de Pascal=== | ===Triángulo de Pascal=== | ||
| - | También conocido como triángulo de [[Tartaglia]]. | ||
| - | |||
| {{Tabla75|celda2= | {{Tabla75|celda2= | ||
| [[Imagen:Triangulo_Pascal.png|thumb|210px|Triángulo de Pascal para ''n=10''.]] | [[Imagen:Triangulo_Pascal.png|thumb|210px|Triángulo de Pascal para ''n=10''.]] | ||
| Línea 49: | Línea 47: | ||
| {{p}} | {{p}} | ||
| }} | }} | ||
| - | {{p}}<br>Es llamado así en honor al matemático francés [[Pascal|Blaise Pascal]], quien introdujo esta notación en 1654, en su ''Traité du triangle arithmétique''. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, en los siglos X y XI, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta. | + | {{p}}Es llamado así en honor al matemático francés [[Pascal|Blaise Pascal]], quien introdujo esta notación en 1654, en su ''Traité du triangle arithmétique''. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, en los siglos X y XI, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta. |
| + | También conocido como '''triángulo de Tartaglia''', especialmente en Italia, en honor al algebrista italiano[[ Tartaglia | Niccolò Fontana Tartaglia]] (1500–77). | ||
| <br> | <br> | ||
| {{Teorema|titulo=Propiedades|enunciado= | {{Teorema|titulo=Propiedades|enunciado= | ||
Revisión de 19:01 4 sep 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Binomio de Newton
Teorema: Fórmula del binomio de Newton
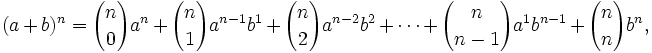
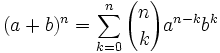
|
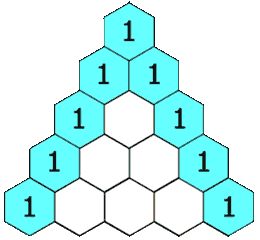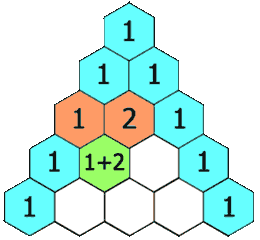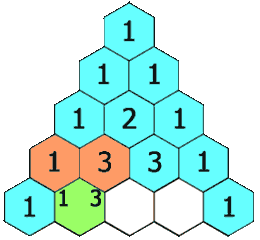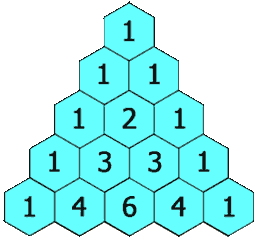
Triángulo de Pascal
|
El triángulo de Pascal es una representación de los coeficientes binomiales 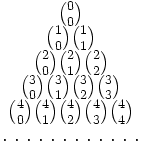 También conocido como triángulo de Tartaglia, especialmente en Italia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–77).
Propiedades
Demostración:
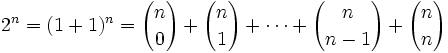
|
|
Actividad: Binomio de Newton
Solución: Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión:
|
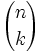 , los
, los 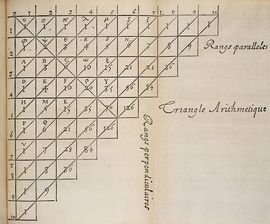
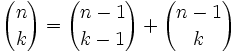 . [1]
. [1]
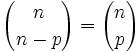 . [2]
. [2]