Plantilla:Números compuestos y números primos
De Wikipedia
| Revisión de 06:55 6 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:57 6 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Tabla75| | + | {{def numeros primos y compuestos}} |
| - | celda1= | + | |
| - | {{p}}{{Caja_Amarilla|texto= | + | |
| - | Un número natural es '''compuesto''' si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número '''primo'''.}}<br> | + | |
| - | {{Ejemplo_simple|titulo=Ejemplos|contenido= | + | |
| - | *15 es compuesto porque <math>15=3 \cdot 5</math>. | + | |
| - | *Los números 2, 3, 5, 7, 11, 13 son primos.}} | + | |
| - | {{p}} | + | |
| - | {{Teorema_sin_demo|titulo=Propiedad|enunciado=:Un número primo sólo tiene por divisores a la unidad y a él mismo.}} | + | |
| - | |celda2= | + | |
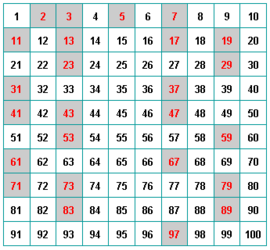
| - | [[Imagen:tabla_primos.png|center|thumb|Números primos menores que 100]] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| {{Video_enlace | {{Video_enlace | ||
Revisión de 06:57 6 sep 2016
Propiedad
Conceptos de número primo y número compuesto. Tabla de números primos menores que 100. Conceptos de número primo y número compuesto. Conceptos de número primo y número compuesto. Breve explicación de qué son los números primos, cómo reconocerlos y cómo encontrarlos fácilmente Conceptos de número primo y número compuesto. Criba de Eratóstenes. Números primos. The building blocks of all natural numbers are the prime numbers. The early Greeks invented the system still used today for separating natural numbers into prime and composite numbers. (Disponibles los subtítulos en inglés) Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado) Determina cuáles de los siguientes números son primos, cuáles son compuestos, y cuáles no son ni primos ni compuestos: 24, 2, 1 y 17. |
- Actividad en la que puedes ver si un número es primo o compuesto.
- Actividad en la que debes separar los números primos de los compuestos.
Introducción a los números primos y compuestos.
Repaso sobre números primos y compuestos.
Actividad en la que aprenderás a determinar si un número es primo o compuesto.
Actividad en la que deberás decidir si un número es primo o compuesto.
Actividad en la que deberás decidir si un número es primo o compuesto.
Actividad en la que deberás pulsar sobre los números primos.
Identifica números primos.
Identifica números compuestos.
Test de 10 preguntas sobre números primos y compuestos.
Ejercicios de autoevaluación sobre números primos.
Ejercicios de autoevaluación sobre números compuestos.
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)
Criba de Eratóstenes
La criba de Eratóstenes es un algoritmo para hallar números primos que desarrolló el célebre matemático griego Eratóstenes en el siglo III a.C.
|
Actividad Interactiva: Criba de Eratóstenes
1. Practica el algoritmo de la criba de Eratóstenes.
Actividad: La Criba de Eratóstenes es un procedimiento para obtener los primeros números primos.
|
Cómo averiguar si un número es primo
Para averiguar si un número es primo, efectuamos divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que la división sea exacta (entonces no es primo) o el cociente sea menor o igual que el siguiente número primo por el que toca dividir (entonces es primo).
Ejemplo: Averiguar si un número es primo
- Averigua si el número 167 es primo.
Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:
- Dividimos 167 entre 2: cociente=83 y resto=1. No es divisible por 2.
- Dividimos 167 entre 3 porque 83>3: cociente=55 y resto=2. No es divisible por 3.
- Dividimos 167 entre 5 porque 55>5: cociente=33 y resto=2. No es divisible por 5.
- Dividimos 167 entre 7 porque 33>7: cociente=23 y resto=6. No es divisible por 7.
- Dividimos 167 entre 11 porque 23>11: cociente=15 y resto=2. No es divisible por 11.
- Dividimos 167 entre 13 porque 15>13: cociente=12 y resto=11. No es divisible por 13.
- Paramos y no dividimos 167 entre 17 porque 12<17.
|
Actividad Interactiva: Números primos y compuestos
1. Descubre si un número es primo o compuesto.
Actividad: Marca el número que quieras en la ventana del control inferior y pulsa intro, después puedes ir variando el valor del número de uno en uno utilizando los triángulos arriba y abajo. El ordenador te indicará si ese número es primo o compuesto. En caso de ser compuesto te indicará además por qué número se le puede dividir después del 1. El número más grande que puedes marcar es el 10.000.000.000 Investiga y contesta en tu cuaderno: a) Desde el número 2, utilizando el triángulo arriba, aumenta de uno en uno y cuenta los números primos que hay en la primera centena desde el 2 hasta el 101. b) Marca después un número de 9 cifras, comienza con uno que termine en 00, aumenta de uno en uno y haz el recuento de los números primos que encuentres en esa centena. c) ¿Qué deduce? |
|
Actividad: Números primos y compuestos
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|