Divisibilidad
De Wikipedia
| Revisión de 23:07 16 abr 2007 Coordinador (Discusión | contribuciones) (→Números compuestos y números primos) ← Ir a diferencia anterior |
Revisión de 23:09 16 abr 2007 Coordinador (Discusión | contribuciones) (→Números compuestos y números primos) Ir a siguiente diferencia → |
||
| Línea 71: | Línea 71: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Un número natural es '''compuesto''' si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número '''primo'''.}}<br> | Un número natural es '''compuesto''' si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número '''primo'''.}}<br> | ||
| - | Un número primo sólo tiene por divisores a la unidad y a él mismo. | + | Un número primo sólo tiene por divisores a la unidad y a él mismo.<br> |
| Por ejemplo, 15 es compuesto porque <math>15=3 \cdot 5</math>. Sin embargo, los números como 2, 3, 5, 7, 11, 13 son primos. | Por ejemplo, 15 es compuesto porque <math>15=3 \cdot 5</math>. Sin embargo, los números como 2, 3, 5, 7, 11, 13 son primos. | ||
| - | (Un número primo sólo tiene por divisores a la unidad y a él mismo) | + | |
| ===Criba de Eratóstenes=== | ===Criba de Eratóstenes=== | ||
| La [http://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes criba de Eratóstenes] es un algoritmo para hallar números primos que desarrolló el célebre matemático griego [http://es.wikipedia.org/wiki/Erat%C3%B3stenes Eratóstenes] en el siglo III a.C. | La [http://es.wikipedia.org/wiki/Criba_de_Erat%C3%B3stenes criba de Eratóstenes] es un algoritmo para hallar números primos que desarrolló el célebre matemático griego [http://es.wikipedia.org/wiki/Erat%C3%B3stenes Eratóstenes] en el siglo III a.C. | ||
Revisión de 23:09 16 abr 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Divisibilidad m.c.m. M.C.D. | WIRIS Geogebra Calculadora {{{enlaces}}} |
Tabla de contenidos |
Múltiplos y divisores
 es multiplo de
es multiplo de  , y escribiremos
, y escribiremos 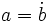 , si existe un número natural
, si existe un número natural  tal que
tal que 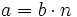 . En tal caso,
. En tal caso,  es divisor de
es divisor de  y escribiremos
y escribiremos 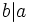
Por ejemplo, 12 es múltiplo de 4 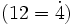 porque
porque 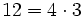 . Por tanto, 4 es divisor de 12
. Por tanto, 4 es divisor de 12 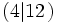 .
.
Propiedades
- Todo número natural es múltiplo de 1 y de sí mismo.
- Todo número natural tiene infinitos múltiplos, que se obtienen multiplicándolo por un número natural cualquiera.
- El 0 es múltiplo de cualquier número.
- Todo número natural tiene, al menos, dos divisores: 1 y él mismo.
Criterios de divisibilidad
Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar una división.
| Divisible por: | Criterio |
|---|---|
| 2 | El número acaba en 0 ó cifra par. |
| 3 | La suma de sus cifras es un múltiplo de 3. |
| 4 | El número formado por las dos últimas cifras es múltiplo de 4. |
| 5 | La última cifra es 0 ó 5. |
| 6 | El número es divisible por 2 y por 3. |
| 8 | El número formado por las tres últimas cifras es múltiplo de 8. |
| 9 | La suma de sus cifras es múltiplo de 9. |
| 10 | La última cifra es 0. |
| 11 | Se suman las cifras que forman el número de forma alternativa y se restan los resultados para ver si da un múltiplo de 11 (El cero también lo es) |
Números compuestos y números primos
Un número natural es compuesto si se puede expresar como producto de otros dos números naturales distintos de él y la unidad. En caso contrario es un número primo.
Un número primo sólo tiene por divisores a la unidad y a él mismo.
Por ejemplo, 15 es compuesto porque 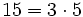 . Sin embargo, los números como 2, 3, 5, 7, 11, 13 son primos.
. Sin embargo, los números como 2, 3, 5, 7, 11, 13 son primos.
Criba de Eratóstenes
La criba de Eratóstenes es un algoritmo para hallar números primos que desarrolló el célebre matemático griego Eratóstenes en el siglo III a.C.
Cómo averiguar si un número es primo
Ejemplo: Averiguar si un número es primo
- Averigua si el número 167 es primo.
Efectuamos las siguientes divisiones por los distintos números primos: 2, 3, 5, 7,... hasta que sea divisible o el cociente sea menor o igual que el siguiente número primo por el que toca dividir:
- Dividimos 167 entre 2: cociente=83 y resto=1. No es divisible por 2.
- Dividimos 167 entre 3 porque 83>3: cociente=55 y resto=2. No es divisible por 3.
- Dividimos 167 entre 5 porque 55>5: cociente=33 y resto=2. No es divisible por 5.
- Dividimos 167 entre 7 porque 33>7: cociente=23 y resto=6. No es divisible por 7.
- Dividimos 167 entre 11 porque 23>11: cociente=15 y resto=2. No es divisible por 11.
- Dividimos 167 entre 13 porque 15>13: cociente=12 y resto=11. No es divisible por 13.
- Paramos y no dividimos 167 entre 17 porque 12<17.

