Plantilla:Raiz de 2 no es racional
De Wikipedia
| Revisión de 12:25 7 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:31 7 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| Pero {{sube|porcentaje=+25%|contenido=<math>a^2\;\!</math>}} es un cuadrado perfecto, o sea es un número entero al cuadrado, luego si uno de sus factores es el 2, el 2 tiene que estar como mínimo al cuadrado, o sea dos veces. | Pero {{sube|porcentaje=+25%|contenido=<math>a^2\;\!</math>}} es un cuadrado perfecto, o sea es un número entero al cuadrado, luego si uno de sus factores es el 2, el 2 tiene que estar como mínimo al cuadrado, o sea dos veces. | ||
| - | Por tanto como ya hay un 2 en la igualdad delante de {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}}, el otro 2 tiene que estar en el {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}} | + | Por tanto como ya hay un 2 en la igualdad delante de {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}}, el otro 2 tiene que estar en el factor {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}} |
| - | Eso quiere decir que {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}} también tiene que ser par, y por tanto {{sube|porcentaje=+20%|contenido=<math>b\;\!</math>}} también es par. | + | Eso quiere decir que {{sube|porcentaje=+20%|contenido=<math>b^2\;\!</math>}} también tiene que ser par, y por tanto, al estar al cuadrado, contener, al menos, dos veces al 2. |
| + | |||
| + | Pero entonces {{sube|porcentaje=+20%|contenido=<math>b\;\!</math>}} contiene un 2, por lo que también es par. | ||
| Pero si {{sube|porcentaje=+10%|contenido=<math>a\;\!</math>}} es par y {{sube|porcentaje=+20%|contenido=<math>b\;\!</math>}} también, la fracción no es irreducible, como habíamos supuesto. | Pero si {{sube|porcentaje=+10%|contenido=<math>a\;\!</math>}} es par y {{sube|porcentaje=+20%|contenido=<math>b\;\!</math>}} también, la fracción no es irreducible, como habíamos supuesto. | ||
Revisión de 12:31 7 sep 2016
Proposición
- No existe ningún número racional que elevado al cuadrado dé como resultado 2. Es decir, el número
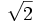 no es racional.
no es racional.
Vamos ha utilizar un tipo de demostración denominado "por reducción al absurdo". Supondremos que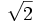 es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
Por tanto, supongamos que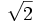 es racional, o sea, que existe una fracción de números enteros
es racional, o sea, que existe una fracción de números enteros  que es igual a
que es igual a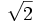 . Dicha fracción la podemos suponer irreducible, ya que siempre es posible simplificarla.
. Dicha fracción la podemos suponer irreducible, ya que siempre es posible simplificarla.
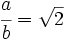
Elevamos al cuadrado los dos miembros de la igualdad:
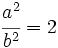
Multiplicamos por 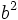 los dos miembros de la igualdad:
los dos miembros de la igualdad:
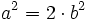
Esta expresión nos dice que 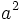 es par, ya que resulta de multiplicar 2 por otro número.
es par, ya que resulta de multiplicar 2 por otro número.
Pero 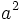 es un cuadrado perfecto, o sea es un número entero al cuadrado, luego si uno de sus factores es el 2, el 2 tiene que estar como mínimo al cuadrado, o sea dos veces.
es un cuadrado perfecto, o sea es un número entero al cuadrado, luego si uno de sus factores es el 2, el 2 tiene que estar como mínimo al cuadrado, o sea dos veces.
Por tanto como ya hay un 2 en la igualdad delante de 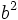 , el otro 2 tiene que estar en el factor
, el otro 2 tiene que estar en el factor 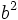
Eso quiere decir que 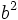 también tiene que ser par, y por tanto, al estar al cuadrado, contener, al menos, dos veces al 2.
también tiene que ser par, y por tanto, al estar al cuadrado, contener, al menos, dos veces al 2.
Pero entonces  contiene un 2, por lo que también es par.
contiene un 2, por lo que también es par.
Pero si  es par y
es par y  también, la fracción no es irreducible, como habíamos supuesto.
también, la fracción no es irreducible, como habíamos supuesto.

