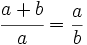Número áureo
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:28 7 sep 2016 Coordinador (Discusión | contribuciones) (→Razón áurea) ← Ir a diferencia anterior |
Revisión de 19:29 7 sep 2016 Coordinador (Discusión | contribuciones) (→Rectángulo áureo) Ir a siguiente diferencia → |
||
| Línea 17: | Línea 17: | ||
| ==Rectángulo áureo== | ==Rectángulo áureo== | ||
| - | El '''rectángulo áureo''' (denominado también rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual a la '''razón áurea'''. Es decir, es aquél rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado | + | El '''rectángulo áureo''' (denominado también rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual al '''número áureo'''. Es decir, es aquél rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado |
Revisión de 19:29 7 sep 2016
El número áureo
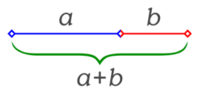
El número áureo, es un número irracional, representado por la letra griega phi φ (en minúscula) o Φ (en mayúscula) en honor al escultor griego Fidias, cuyo valor es:
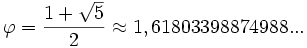 También se le conoce como número de oro o razón áurea o divina proporción (por la obra de Luca Pacioli, De Divina Proportione, escrito entre 1496 y 1498). |
Rectángulo áureo
El rectángulo áureo (denominado también rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual al número áureo. Es decir, es aquél rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado