Número áureo
De Wikipedia
| Revisión de 14:45 8 sep 2016 Coordinador (Discusión | contribuciones) (→El número áureo en el arte y en la cultura) ← Ir a diferencia anterior |
Revisión de 14:45 8 sep 2016 Coordinador (Discusión | contribuciones) (→El número áureo en el arte y en la cultura) Ir a siguiente diferencia → |
||
| Línea 128: | Línea 128: | ||
| *A lo largo de la historia ha fascinado a muchos científicos, artistas, poetas, ... Por ejemplo, encontramos la siguiente cita de Kepler (1571-1630): ''Creo que de esta proporción geométrica se sirvió el Creador como la idea por medio de la que introdujo la generación continua de objetos semejantes a partir de objetos semejantes''. O este soneto que escribió Rafael Alberti cerrando el premio a la obra de Luca Pacioli en la edición de 1949 de la Ed. Losado, S. A., en Buenos Aires: | *A lo largo de la historia ha fascinado a muchos científicos, artistas, poetas, ... Por ejemplo, encontramos la siguiente cita de Kepler (1571-1630): ''Creo que de esta proporción geométrica se sirvió el Creador como la idea por medio de la que introdujo la generación continua de objetos semejantes a partir de objetos semejantes''. O este soneto que escribió Rafael Alberti cerrando el premio a la obra de Luca Pacioli en la edición de 1949 de la Ed. Losado, S. A., en Buenos Aires: | ||
| - | + | <br> | |
| <center>''A ti, maravillosa disciplina,'' | <center>''A ti, maravillosa disciplina,'' | ||
| Línea 156: | Línea 156: | ||
| ''A ti, divina proporción de oro.''</center> | ''A ti, divina proporción de oro.''</center> | ||
| - | + | <br> | |
| *Curiosamente, también aparece en la naturaleza en el crecimiento de algunas plantas, en la distribución de las hojas de algunos tallos, en el crecimiento de las conchas de algunos moluscos. | *Curiosamente, también aparece en la naturaleza en el crecimiento de algunas plantas, en la distribución de las hojas de algunos tallos, en el crecimiento de las conchas de algunos moluscos. | ||
Revisión de 14:45 8 sep 2016
Tabla de contenidos |
El número áureo
El número áureo, es un número irracional cuyo valor es: 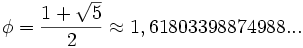 Fue el primer número del que se tuvo conciencia que era irracional. Es representado por la letra griega phi φ (en minúscula) o Φ (en mayúscula) en honor al escultor griego Fidias. También se le conoce como número de oro, razón áurea o divina proporción (por la obra de Luca Pacioli, De Divina Proportione, escrita entre 1496 y 1498). Proposición 1
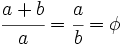 Demostración: Partimos de la proporción dada: 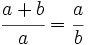 Separamos en dos sumandos el término de la izquierda: 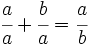 Llamando 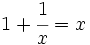 Quitando denominadores y trasponiendo términos: 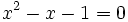 ecuación de segundo grado cuya única raíz válida es: 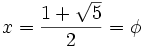 |
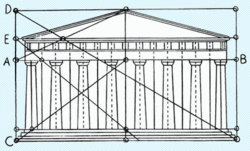
El rectángulo áureo
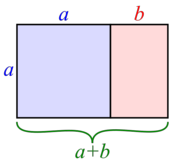
El rectángulo áureo (o rectángulo dorado) es un rectángulo que posee una proporcionalidad entre sus lados igual al número áureo. Los griegos consideraban que un rectángulo de tales características era especialmente armonioso. Esta proporción de medidas se ha utilizado con mucha frecuencia en el arte. Proposición 2
Demostración: Partimos de un rectángulo áureo. Lo dividimos en un cuadrado de lado su lado menor y otro rectángulo pequeño, como se observa en la Fig. 2. Veamos que el rectángulo pequeño también es un rectángulo áureo. Para ello tendremos que comprobar que Por ser el rectángulo de partida un rectángulo áureo, se cumple que la proporción entre sus lados es el número áureo: 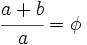 Operando:
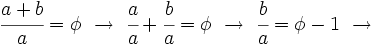 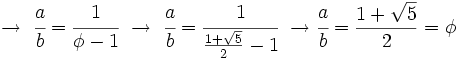 |
Construcción del rectángulo áureo
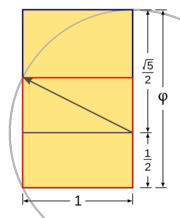
Construcción del rectángulo áureo con regla y compás
Demostración: Si te fijas en la Fig. 3, basta con demostrar que el segmento que se obtiene en el paso 2 mide 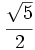 , para lo cual basta con usar el teorema de Pitágoras. , para lo cual basta con usar el teorema de Pitágoras.En la escena puedes ver la construcción del número de oro basada en una construcción gráfica que se encuentra en un libro de Euclides (siglo III a.C.).
Construcción con regla y compás de la sección áurea de un segmento y del rectángulo áureo. |
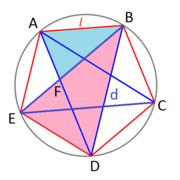
El número áureo en el péntágono estrellado
Los griegos pitagóricos (seguidores de las teorías de Pitágoras) pensaban que el mundo se regía por su orden numérico y geométrico. Para ellos, los únicos números existentes eran los naturales y las relaciones entre ellos (fracciones). Su emblema era la estrella de cinco puntas o pentágono estrellado. Esta estrella representaba la vida y, puesta con una de sus vértices hacia abajo, representa lo contrario (lo maléfico). Comprobaron que en un pentágono regular, la relación entre su diagonal y su lado es el número áureo. Cuando llegaron a la conclusión de que esta relación no se podía expresar como cociente de dos números enteros, se quedaron espantados, y les pareció tan contrario a toda lógica que lo llamaron irracional. Es el primer número irracional del que se tuvo conciencia que lo era.
El número áureo en el péntágono estrellado
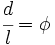 Demostración:
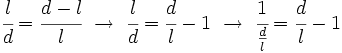
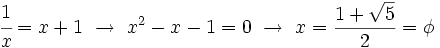 |
La sucesión de Fibonacci y el número áureo
La sucesión de Fibonacci se debe a Leonardo de Pisa (Fibonacci), matemático italiano del siglo XIII. Es la siguiente:
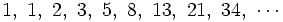
Es una sucesión recurrente dada por la siguiente relación de recurrencia:
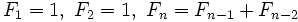
Término general de la sucesión de Fibonacci
El término general de la sucesión de Fibonacci es:
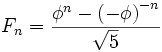
siendo 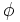 el número áureo.
el número áureo.
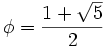
Puedes ver una demostración que sobrepasa este nivel en este enlace: enlace a wikipedia
La sucesión de Fibonacci y el número áureo
Si a partir de la sucesión de Fibonacci
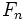 = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...,
= 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...,construimos, por recurrencia, la sucesión
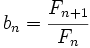
Entonces, esta sucesión tiende al número áureo:

Comprobación: Si en la sucesión de Fibonacci
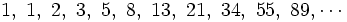
dividimos cada término entre el anterior, tenemos:
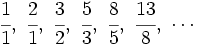
que expresada con decimales nos da:
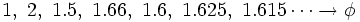
Demostración:
Por construcción de la sucesión de Fibonacci:
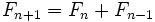
Dividiendo ambos miembros por 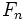 :
:
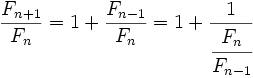
Tomando límites en ambos miembros:
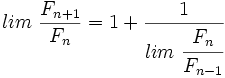
Llamando 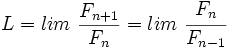 , tenemos:
, tenemos:
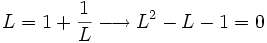
ecuación de segundo grado cuya única raíz válida es:
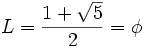
El número áureo en la naturaleza
Ejemplo: La sucesión de Fibonacci y el número áureo
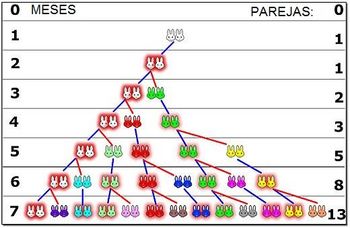
El siguiente problema fue propuesto por Fibonacci, matemático italiano del siglo XIII:
- "Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?"
a) Escribe la sucesión cuyos términos son lás parejas de conejos que hay cada més. Esta recibe el nombre de sucesión de Fibonacci.
b) Ahora vas a construir la sucesión que se obtiene al dividir cada término entre el anterior. Esa sucesión verás que se aproxima al número áureo (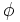 ):
):
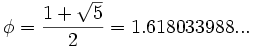
a) Sucesión de Fibonacci:
- Mes 1: 1 pareja (la pareja nace al comenzar el primer mes)
- Mes 2: 1 pareja (la pareja no es fértil hasta que termine el 2º mes)
- Mes 3: 2 parejas (al comenzar el tercer mes se reproduce por primera vez)
- Mes 4: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el comienzo del próximo mes)
- Mes 5: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no)
- Mes 6: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no)
- Mes 7: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no)
Así se obtiene la sucesión de Fibonacci, en la que cada término se obtiene a partir de la suma de los dos anteriores:
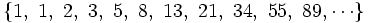
b) Sucesión del número áureo:
Dividiendo cada término entre el anterior, tenemos la sucesión:
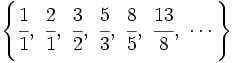
que expresada con decimales vemos que se aproxima al número áureo:
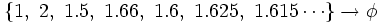
Nota: Leonardo de Pisa (Fibonacci), en su Libro de los ábacos (Liber abacci, 1202, 1228), usa la sucesión que lleva su nombre para calcular el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos están aislados por muros, se empiezan a reproducir cuando tienen dos meses de edad, tardan un mes desde la fecundación hasta la parición y cada camada es de dos conejos). Este es un problema matemático puramente independiente de que sean conejos los involucrados. En realidad, el conejo común europeo tiene camadas de 4 a 12 individuos y varias veces al año, aunque no cada mes, pese a que la preñez dura 32 días. El problema se halla en las páginas 123 y 124 del manuscrito de 1228, que fue el que llegó hasta nosotros, y parece que el planteamiento recurrió a conejos como pudiera haber sido a otros seres; es un soporte para hacer comprensible una incógnita, un acertijo matemático.
Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
Grandes temas de la matemática - Capítulo 4: Fibonacci. (con Adrian Paenza)
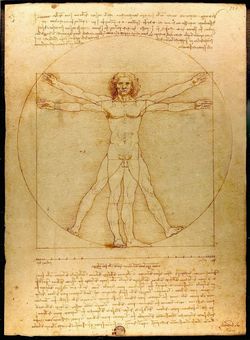
El número áureo en el arte y en la cultura
media, extrema razón de la hermosura, que claramente acata la clausura viva en la malla de tu ley divina. A ti, cárcel feliz de la retina, áurea sección, celeste cuadratura, misteriosa fontana de mesura que el universo armónico origina. A ti, mar de los sueños angulares, flor de las cinco formas regulares, dodecaedro azul, arco sonoro. Lucas por alas un compás ardiente. Tu canto es una esfera transparente. A ti, divina proporción de oro.
|
Videos y páginas web
Documental sobre el número aureo.
El programa presenta a este exótico número ya conocido por los griegos. Veremos cómo se obtiene, qué son los rectángulos áureos y su presencia en infinidad de manifestaciones artísticas, en Pintura, Arquitectura, Escultura... a lo largo de la historia. Pero el número de oro no es un mero invento del hombre, la naturaleza nos sorprende de una forma que no puede ser casual, tanto en el mundo vegetal como en el animal, como en multitud de fenómenos físicos, con acontecimientos en los que este famosos número hace acto de presencia.
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.
Leonardo de Pisa, más conocido como Fibonacci, es el autor de la primera summa matemática de la Edad Media, el Liber Abaci. Con este libro introduce en la Europa cristiana las nueve cifras hindúes y el signo del cero. Pero además brinda a los calculistas de la época reglas claras para realizar operaciones con estas cifras tanto con números enteros como con fracciones. Pero Fibonacci es más conocido entre los matemáticos por la curiosa sucesión de números que lleva su nombre y en la que cada término es la suma de los dos anteriores. Esta sucesión es una auténtica fuente de agradables sorpresas. Analizaremos las sugerentes relaciones que existen entre sus términos y descubriremos su presencia en fenómenos naturales coma la ramificación de algunas plantas, la distribución de los piñones en las piñas y de las pipas en los girasoles. Y, aunque en principio cueste trabajo creérselo, veremos que está directamente emparentada con un viejo amigo nuestro: el número áureo.
Grandes temas de la matemática - Capítulo 4: Fibonacci. (con Adrian Paenza)
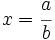 , tenemos que
, tenemos que 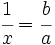 , de manera que:
, de manera que:
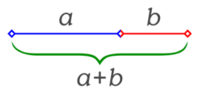
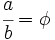
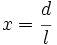 :
: