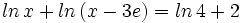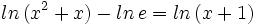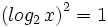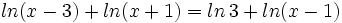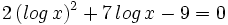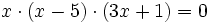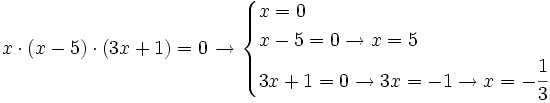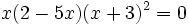Resolución de ecuaciones (1ºBach)
De Wikipedia
| Revisión de 17:17 9 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:33 9 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios) Ir a siguiente diferencia → |
||
| Línea 97: | Línea 97: | ||
| |titulo=Ejercicios propuestos: ''Resolución de ecuaciones'' | |titulo=Ejercicios propuestos: ''Resolución de ecuaciones'' | ||
| |cuerpo= | |cuerpo= | ||
| - | (pág. ) | + | (pág. 80 ) |
| - | :[[Imagen:red_star.png|12px]] 3a,c,f; 4a,b; 5; 6 | + | :[[Imagen:red_star.png|12px]] 2a,c; 3a,c,f; 4a,b; 5; 6 |
| - | :[[Imagen:yellow_star.png|12px]] 3b,d,e; 4c,d,e,f | + | :[[Imagen:yellow_star.png|12px]] 2b,d; 3b,d,e; 4c,d,e,f |
| }} | }} | ||
Revisión de 17:33 9 sep 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Test de Álgebra | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Ecuación de segundo grado
- Una ecuación de segundo grado con una incógnita,
 , es aquella que tiene o se puede reducir a la siguiente expresión, que llamaremos forma general.
, es aquella que tiene o se puede reducir a la siguiente expresión, que llamaremos forma general.
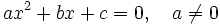
- Si algún coeficiente,"b" o "c", es cero la ecuación diremos que es incompleta. En caso contrario diremos que es completa.
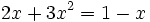 es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: 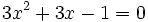
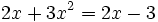 es una ecuación de segundo grado incompleta, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado incompleta, ya que se puede reducir a la siguiente forma general: 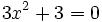
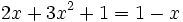 es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general:
es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: 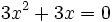
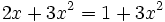 no es una ecuación de segundo grado, ya que al reducirla resulta una ecuación de primer grado:
no es una ecuación de segundo grado, ya que al reducirla resulta una ecuación de primer grado: 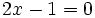
Definición de ecuación de segundo grado.
Actividades en la que aprenderás a identificar los coeficientes de una ecuación de segundo grado y a determinar si es completa o incompleta.
El siguiente videotutorial condensa casi todo lo que se va a tratar en este tema:
- Definición de ecuación de segundo grado.
- Fórmula para su resolución con su demostración.
- Definición de discriminante de una ec. de segundo grado y su relación con el número de soluciones de ésta y con ejemplos de cada caso.
- Factorización del polinomio de segundo grado a partir de las soluciones o raíces de la ecuación de segundo grado.
- Propiedades del producto y la suma de las raíces de la ecuación con su demostración.
- Ecuaciones de segundo grado incompletas.
Ecuación de segundo grado completa
Fórmula general
Las soluciones de la ecuación de segundo grado
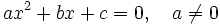
son:
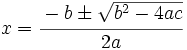
donde el signo 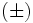 significa que una solución se obtiene con el signo
significa que una solución se obtiene con el signo 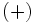 y otra con el signo
y otra con el signo 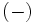 .
.
A continuación tienes la demostración en videtutorial y por escrito:
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas.
Demostración:
1. Se divide la ecuación por  :
:
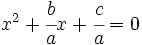
2. Se multiplica y divide por  el coeficiente de la
el coeficiente de la  :
:
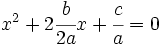
3. Se suma a los dos miembros de la igualdad 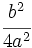 :
:
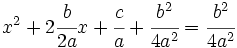
4. Se pasa restando a la derecha  :
:
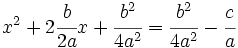
5. Observando que el lado izquierdo es el desarrollo de 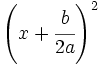 :
:
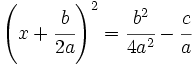
6. Se extrae la raíz cuadrada en ambos miembros:
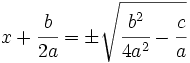
7. Se despeja x:
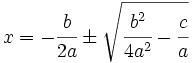
8. Se simplifica la expresión:
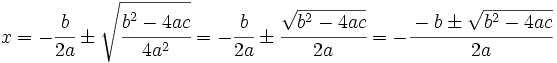
En la escena, pulsa "Inicio" para ver otros ejemplos.
Cómo utilizar la fórmula general de la ecuación de segundo grado.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Tutorial en el que se explica la resolución de ecuaciones de 2º grado aplicando la fórmula general de resolución.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Resolución de ecuaciones de segundo grado completas mediante la fórmula. Ejemplos.
Escribe en forma general e identifica los coeficientes "a", "b", y "c": 6x2 + 3 = 2x − 6.
Resuelve usando la fórmula: − x2 + 8x = 1.
Resuelve usando la fórmula: − 3x2 + 10x − 3 = 0.
Resuelve usando la fórmula: − 7q2 + 2q + 9 = 0.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado completas.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado completas.
Resolver ecuaciones de segundo grado completas.
Ejercicios de autoevaluación sobre ecuaciones de segundo grado completas.
- Pulsa el botón "Ejercicio" para obtener una ecuación.
- Copia la ecuación en tu cuaderno y halla sus soluciones.
- Escribe el "tipo de solución" y las soluciones en los cuadros correspondientes. Luego pulsa el botón "Solución".
Ejercicios resueltos sobre ecuaciones de segundo grado completas.
Número de soluciones de la ecuación de segundo grado
Llamamos discriminante de una ecuación de segundo grado, 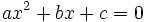 , al número:
, al número:
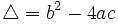
Proposición
Sea  el discriminante de una ecuación de segundo grado:
el discriminante de una ecuación de segundo grado:
- Si
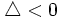 , la ecuación no tiene solución.
, la ecuación no tiene solución.
- Si
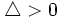 , la ecuación tiene dos soluciones.
, la ecuación tiene dos soluciones.
- Si
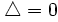 , la ecuación tiene una solución (doble).
, la ecuación tiene una solución (doble).
La demostración es inmediata teniendo en cuenta la fórmula para la resolución de la ecuación de segundo grado:
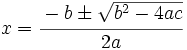
ya que, lo que hay en el radicando, es precisamente el discriminante. Por tanto,
- Si su signo es positivo, la raíz existe y da lugar a dos soluciones distintas.
- Si su signo es negativo, la raíz no existe y no hay ninguna solución.
- Si es cero, la raíz vale cero, y hay dos soluciones iguales (solución doble).
Número de soluciones de una ecuación de 2º grado. Discriminante.
Halla el discriminante para determinar el número de raíces de la ecuación 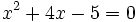 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 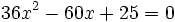 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 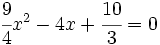 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 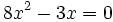 .
.
Halla el discriminante para determinar el número de raíces de la ecuación 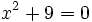 .
.
Determinar el número de soluciones de la ecuación 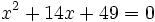 .
.
Actividades en la que aprenderás a calcular el discriminante de una ecuación de segundo grado y su utilidad para determinar el número de soluciones de la misma.
Calcula el número de soluciones de una ecuación de segundo grado:
- Pulsa el botón "Ejercicio" para obtener una ecuación.
- Copia la ecuación en tu cuaderno y calcula su discriminante.
- Teniendo en cuenta el valor del discriminante, determina cuántas soluciones tiene.
- Escribe el número de soluciones en el cuadro "Número de soluciones" y pulsa el botón "Solución".
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado, 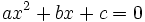 , es incompleta, si
, es incompleta, si 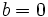 ó
ó 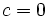 :
:
- Si
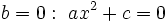
- Si
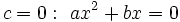
Resolución de las ecuaciones de segundo grado incompletas
- En el caso
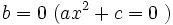 , las soluciones se obtienen despejando
, las soluciones se obtienen despejando  :
:
- En el caso
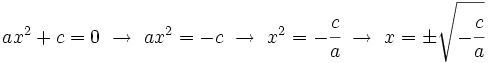
- En el caso
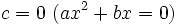 , las soluciones se obtienen sacando factor común e igualando a cero cada factor:
, las soluciones se obtienen sacando factor común e igualando a cero cada factor:
- En el caso
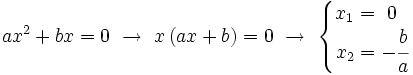
En la escena, pulsa "INICIO" para ver otros ejemplos.
En la escena, pulsa "INICIO" para ver otros ejemplos.
Ecuaciones de segundo grado sin termino lineal (caso b=0). Ejemplos.
Ecuaciones de segundo grado sin termino independiente (caso c=0). Ejemplos.
Ecuaciones de segundo grado incompletas (caso b=0)
Ecuaciones de segundo grado incompletas (caso c=0)
Ecuaciones de segundo grado incompletas (caso b=0):
Resuelve: 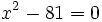
Resuelve: 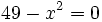
Resuelve: 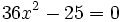
Resuelve: 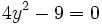
Ecuaciones de segundo grado incompletas (caso c=0):
Resuelve: 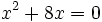
Resuelve: 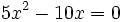
Resuelve: 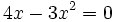
Actividades en la que aprenderás a resolver ecuaciones de segundo grado incompletas del tipo b=0.
Actividades en la que aprenderás a resolver ecuaciones de segundo grado incompletas del tipo c=0.
Ejercicios de autoevaluación sobre ecuaciones de segundo grado incompletas.
Ejercicios resueltos sobre ecuaciones de segundo grado incompletas.
Videotutoriales
- Definición de ecuación de segundo grado.
- Fórmula para su resolución con su demostración.
- Definición de discriminante de una ec. de segundo grado y su relación con el número de soluciones de ésta y con ejemplos de cada caso.
- Factorización del polinomio de segundo grado a partir de las soluciones o raíces de la ecuación de segundo grado.
- Propiedades del producto y la suma de las raíces de la ecuación con su demostración.
- Ecuaciones de segundo grado incompletas.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Ecuaciones bicuadradas
(pag. 78)
Las ecuaciones bicuadradas son ecuaciones de cuarto grado que no tienen terminos de grado impar, es decir son de la forma
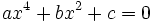
Resolución de la ecuación bicuadrada
El método para resolver una ecuación bicuadrada
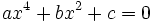
consiste en hacer el cambio de variable 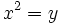 . Entonces, nos quedará la siguiente ecuación de segundo grado en "y".
. Entonces, nos quedará la siguiente ecuación de segundo grado en "y".
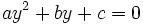
Una vez resuelta esta ecuación en "y", tenemos que averiguar el valor de la "x". Para ello desharemos el cambio de variable, haciendo 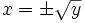 . En consecuencia, las soluciones
. En consecuencia, las soluciones 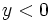 , las rechazaremos, ya que no darán solución para la
, las rechazaremos, ya que no darán solución para la 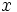 , quedándonos sólo con las soluciones de
, quedándonos sólo con las soluciones de 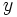 no negativas, cada una de las cuales dará dos soluciones para la
no negativas, cada una de las cuales dará dos soluciones para la 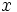 .
.
En consecuencia, una ecuación bicuadrada tendrá, como máximo, cuatro soluciones reales.
Ejercicios resueltos: Ecuaciones bicuadradas
Resuelve las ecuaciones:
- a)
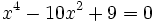
- b)
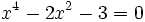
- c)
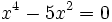
a)
- Soluciones:
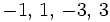
b)
- Soluciones:
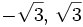
c)
- Soluciones:
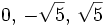
Ecuaciones bicuadradas. Ejemplos.
Tutorial que explica de forma completa la resolución de ecuaciones bicuadradas, resolviendo muchos ejercicios desde muy sencillos, para entender mejor la estrategia a seguir, hasta más completos.
- 00:00 a 04:55: Conceptos teóricos de la resolución de ecuaciones de grado mayor que 2. Método de Factorización.
- 04:55 a 27:27: Ejercicios de ecuaciones bicuadradas o que pueden resolverse con este método.
- Método de resolución de ecuaciones bicuadradas.
- Ejemplos.
Método de resolución de ecuaciones bicuadradas. Ejemplos.
Resuelve y factoriza: 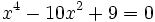
Resuelve:
a) 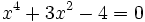
b) 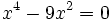
c) 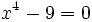
d) 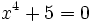
e) 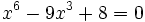
Ecuaciones con fracciones algebaricas
(pág. 78)
Las ecuaciones con fracciones algebraicas, son aquellas en las que intervienen fracciones algebraicas y, por tanto, las incógnitas aparecen en algún denominador.
Resolución de las ecuaciones con fracciones algebraicas
Estas ecuaciones se pueden resolver de forma análoga a las que tienen números en el denominador, multiplicando los dos miembros de la ecuación por el m.c.m. de los polinomios de los denominadores y simplificando (se divide el m.c.m. entre cada denominador y se multiplica el resultado por su respectivo numerador). De esta forma desaparecen los denominadores y la ecuación resultante ya es más sencilla de resolver.
En estos procesos de multiplicar los miembros de la ecuación por polinomios, pueden aparecer soluciones falsas. Por tanto, al terminar, siempre debemos comprobar todas las posibles soluciones obtenidas.
Ejercicio resuelto: Ecuaciones con fracciones algebraicas
Resuelve las ecuación: 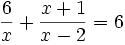
El m.c.m. de los denominadores es 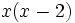 . Multiplicamos ambos miembros por el m.c.m. (o equivalentemente, dividimos el m.c.m. por cada denominador y multiplicamos el resultado por el numerador).
. Multiplicamos ambos miembros por el m.c.m. (o equivalentemente, dividimos el m.c.m. por cada denominador y multiplicamos el resultado por el numerador).
Simplificamos:
Y la resolvemos:
Ambas soluciones, tras ser comprobadas en la ecuación inicial, resultan ser válidas.
Soluciones: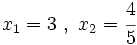
Ecuaciones con fracciones algebraicas. Ejemplos
Tutorial que explica de forma completa la resolución de ecuaciones con quebrados algebraicos, que son aquellas que tienen expresiones algebraicas en el denominador, resolviendo muchos ejercicios desde muy sencillos, para entender mejor la estrategia a seguir, hasta más completos.
Ejercicios de ecuaciones con radicales:
- (01:03)
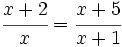
- (05:00)
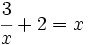
- (10:00)
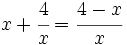
- (14:56)
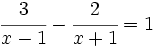
- (20:28)
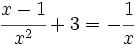
- (25:00)
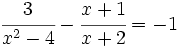
Ecuaciones racionales, que son aquellas con la x en el denominador.
Resuelve: 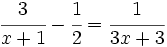
Resuelve: 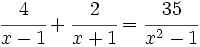
Resuelve: 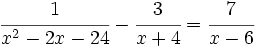
Resuelve: 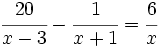
Resuelve: 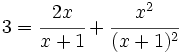
Resuelve: 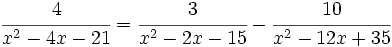
Resuelve: 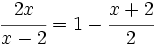
Resuelve: 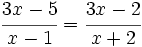
|
Actividad: Ecuaciones con fracciones algebraicas Resuelve las siguientes ecuaciones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ecuaciones con radicales
(pág. 79)
Las ecuaciones con radicales o ecuaciones irracionales son aquellas que tienen la incógnita bajo el signo radical.
Resolución de las ecuaciones radicales
Para resolver las ecuaciones con radicales hay que aislar las raices, una a una, e ir elevando al cuadrado ambos miembros de la ecuación para eliminarlas.
Al elevar al cuadrado para buscar la solución, pueden aparecer soluciones erroneas. Por eso, al finalizar, hay que hacer la comprobación en la ecuación inicial para detectar y recharzar las que no sean válidas.
Ejercicios resueltos: Ecuaciones con radicales
Resuelve las ecuaciones:
- a)
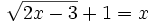
- b)
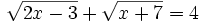
a) 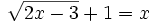
Aislamos la raíz:
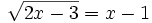
Se elevan al cuadrado los dos lados de la ecuación:
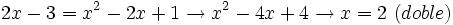
Comprobación: 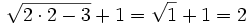
Luego es válida  .
.
b) 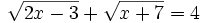
Aislamos una de las dos raíces:
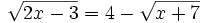
Se elevan al cuadrado los dos lados de la ecuación:
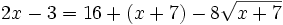
Aislamos la raíz:
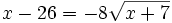
Se elevan al cuadrado los dos lados de la ecuación:
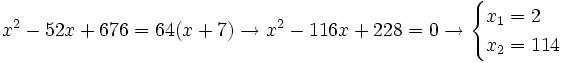
Comprobación: 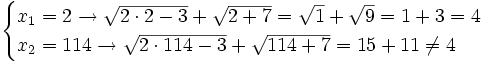
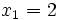
Ecuaciones con radicales. Ejemplos.
Tutorial que explica de forma completa la resolución de ecuaciones con radicales, resolviendo muchos ejercicios desde muy sencillos, para entender mejor la estrategia a seguir, hasta más completos.
- 1) (00:57)
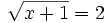
- 2) (03:10)
![\sqrt[3]{x-2}+2 =0\;](/wikipedia/images/math/d/4/a/d4add67bb84f722d8cb6a162e6f59344.png)
- 3) (04:40)
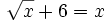
- 4) (11:28)
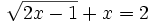
- 5) (14:12)
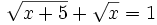
- 6) (19:20)
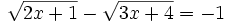
Ecuaciones irracionales, que son aquellas con radicales.
Ecuaciones irracionales, que son aquellas con radicales.
Resuelve: a) b) Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: | Resuelve: Resuelve: Resuelve: Resuelve: 3 ecuaciones con radicales. |
Ecuaciones exponenciales
(pág. 79)
Las ecuaciones exponenciales son aquellas en las que la incógnita aparece como exponente.
Para su resolución hay que tener en cuenta las propiedades de las potencias y también puede ser necesario usar logaritmos.
Ejercicios resueltos: Ecuaciones exponenciales
Resuelve las siguientes ecuaciónes:
- a)
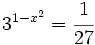
- b)
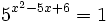
- c)
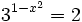
- d)
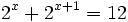
a)
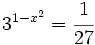
Expresamos el segundo miembro como potencia de 2:
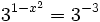
Como 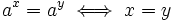 , los exponentes deben ser iguales:
, los exponentes deben ser iguales:
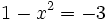
Y resolvemos la ecuación de segundo grado incompleta:
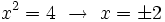
Soluciones: 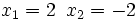
b)
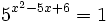
Expresamos el segundo miembro como potencia de 5:
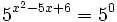
Como 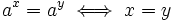 , los exponentes deben ser iguales:
, los exponentes deben ser iguales:
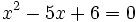
Resolvemos la ecuación de segundo grado:
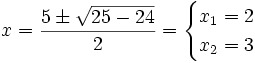
Soluciones: 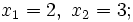
c)
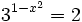
Como el segundo miembro no podemos expresarlo como potencia de base 3, tomaremos logaritmos en ambos lados de la ecuación:
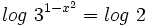
Aplicando la propiedad del logaritmo de una potencia:
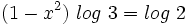
Y resolvemos la ecuación de segundo grado incompleta:
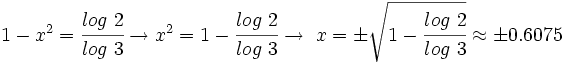
Soluciones: 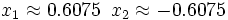
d)
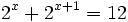
Haciendo el cambio de variable:
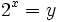
tenemos que:
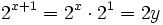
Y la ecuación de partida queda:
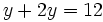
Resolvemos la ecuación de primer grado:
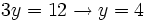
Y deshacemos el cambio de variable:
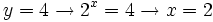
- Solución:

Tutorial que trabaja las ecuaciones exponenciales, desde muy sencillas, en donde únicamente se utilizan las propiedades básicas de las potencias, hasta otras más completas en donde es necesario realizar un cambio de variable.
- 00:00 a 01:15: Introducción y propiedad.
- 01:15 a 07:00: Ejercicios básicos, resolubles con las propiedades de las potencias.
- 07:00 a 11:55: Ejercicios de ecuaciones exponenciales usando el cambio de variable (primer grado).
- 11:55 a 22:26: Ejercicios de ecuaciones exponenciales usando el cambio de variable (segundo grado).
Ecuaciones exponenciales, que son aquellas con la x en el exponente.
Ejemplos de resolución de ecuaciones exponenciales.
Más ejemplos de resolución de ecuaciones exponenciales.
Resuelve:
Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Resuelve: Resuelve: | Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: |
Ejercicios resueltos sobre ecuaciones exponenciales.
|
Actividad: Ecuaciones exponenciales Resuelve las siguientes ecuaciones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ecuaciones logarítmicas
(pág. 80)
Las ecuaciones logarítmicas son aquellas en las que la incógnita aparece como parte de un logaritmo.
Para su resolución hay que tener en cuenta las propiedades de los logaritmos.
Se deben comprobar siempre las soluciones en la ecuación de partida pues pueden obtenerse soluciones que no sean válidas, como puede verse en el ejemplo c) siguiente.
Ejemplos: Ecuaciones logarítmicas
Resuelve las siguientes ecuaciónes:
- a)
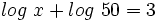
- b)
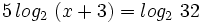
- c)
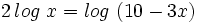
a)
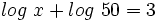
Teniendo en cuenta que 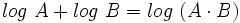 y que
y que 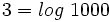 , tenemos:
, tenemos:
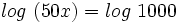
Y teniendo en cuenta que 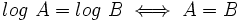 , se tiene:
, se tiene:
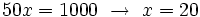
La solución se comprueba en la ecuación de partida y resulta ser válida.
Solución: 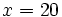
b)
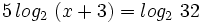
Teniendo en cuenta que 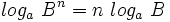 y que
y que 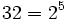 :
:
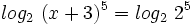
Como 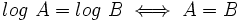 , se tiene:
, se tiene:
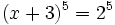
Y, como 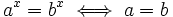
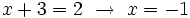
Se comprueba en la ecuación de partida y resulta ser válida.
Solución: 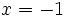
c)
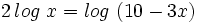
Teniendo en cuenta que 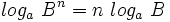 , tenemos:
, tenemos:
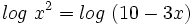
Como 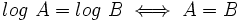 , se tiene:
, se tiene:
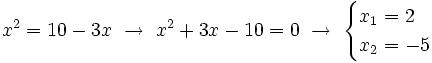
De las dos soluciones, 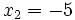 no es válida, porque al comprobarla en la ecuación de partida,
no es válida, porque al comprobarla en la ecuación de partida, 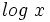 no se puede calcular para
no se puede calcular para 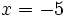 (El logaritmo de un número negativo no existe).
(El logaritmo de un número negativo no existe).

Tutorial que trabaja las ecuaciones logarítmicas, desde muy sencillas que se resuelven utilizando únicamente la definición, hasta otras más completas.
- 00:00 a 02:36: Repaso de las propiedades de los logaritmos.
- 02:36 a 08:20: Ejercicios "base" para resolver ecuaciones.
- 08:20 a 11:55: Ejercicios básicos de ecuaciones logarítmicas, usando la definición de logaritmo.
- 11:55 a 21:07: Ejercicios de ecuaciones logarítmicas.
Ecuaciones logarítmicas.
Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve:
Resuelve: | Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: |
Ejercicios resueltos sobre ecuaciones logarítmicas.
|
Actividad: Ecuaciones logarítmicas Resuelve las siguientes ecuaciones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
Nota: En WolframAlpha log y loge simbolizan el logaritmo neperiano mientras que el logaritmo decimal es log10. |
(pág. 80)
Ecuaciones factorizadas
Las ecuaciones factorizadas son ecuaciones del tipo:
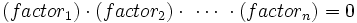
donde cada factor puede ser una expresión algebraica, logarítmica, exponencial, trigonométrica, o combinación de estas.
Resolución de las ecuaciones factorizadas
Como para que un producto de números reales sea cero basta con que uno de ellos sea cero, las soluciones se obtendrán igualando a cero cada uno de los factores y resolviendo la ecuación resultante. Dependiendo de como sea cada factor tendremos que aplicar alguna de las distintas técnicas estudiadas anteriormente.
Ejercicios
|
Ejercicios propuestos: Resolución de ecuaciones |
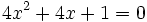
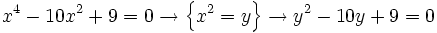
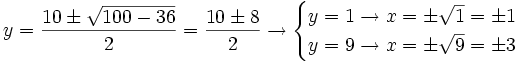
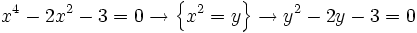
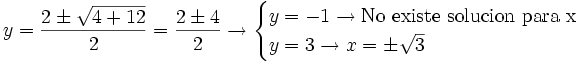
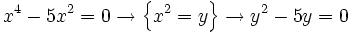
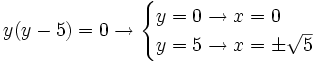
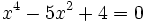
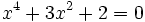
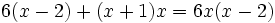
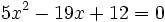
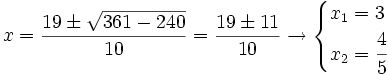
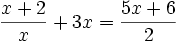
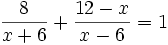
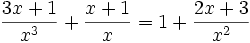
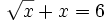
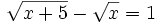
![7+\sqrt[3]{5x-2}=9\;](/wikipedia/images/math/6/a/f/6af645df30220f04516e2fc14bef6f9a.png)
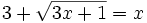
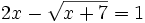
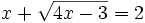
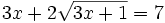
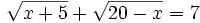
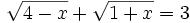
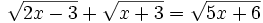
![\sqrt[3]{x+3}=\sqrt{x-1}\;](/wikipedia/images/math/b/0/4/b04567c4f2bc400f01cf3b70e3100545.png)
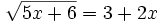
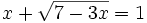
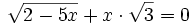
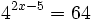
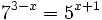
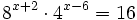
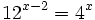
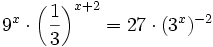
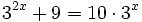
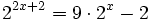
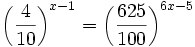
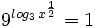
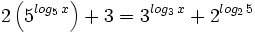
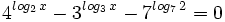
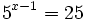
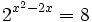
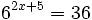
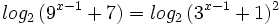
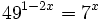
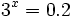
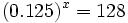
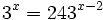
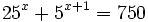
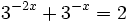
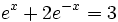
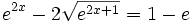
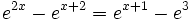
![3^x=\sqrt[3]{9} \;](/wikipedia/images/math/d/b/0/db0233292d84043ca9d4101f6ac692a6.png)
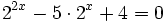
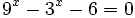
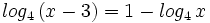
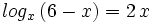
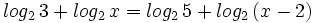
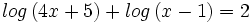
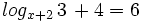
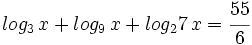
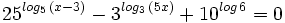
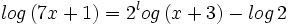
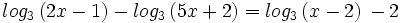
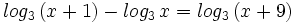
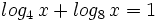
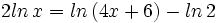
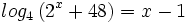
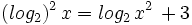
![log \, \sqrt[3]{x} = \sqrt{log \, x}\;](/wikipedia/images/math/6/c/c/6cc126bf04f02f1123358336f576a013.png)
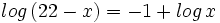
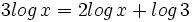
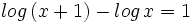
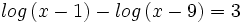
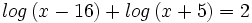
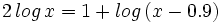
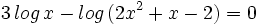
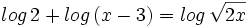
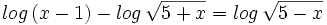
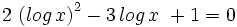
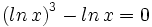
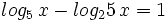
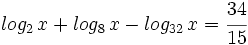
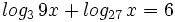
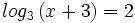
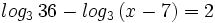
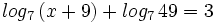
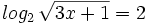
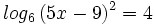
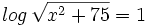
![log_6 \, \sqrt[3]{4x-1}=log_6 \, \sqrt[3]{9}+log_6 \, \sqrt[3]{x-4} \;](/wikipedia/images/math/6/9/3/693f53a3f8089ea15b162093daf2ef62.png)