Sistemas de numeración (1º ESO)
De Wikipedia
| Revisión de 14:13 18 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 11:39 25 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 37: | Línea 37: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/ciclo1/01.htm | + | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/01.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/ciclo1/01.htm | + | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/01.htm |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:39 25 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 8)
Sistemas de numeración
| Los números surgen de la necesidad de contar. Por ejemplo, el hombre primitivo, para contar los animales de su rebaño, hacia uso de semillas o guijarros; muescas en palos, huesos o piedras; etc.
En numerosas civilizaciones el hombre uso su cuerpo, dándole a sus partes (manos, pies, falanges, ...) valores numéricos. A medida que la sociedad fue evolucionando, surgió la necesidad de contar cantidades más grandes, para lo que hubo que inventar nuevos símbolos. Los símbolos utilizados para representar los números y sus normas de uso forman un sistema de numeración. |  |
Tipos de sistemas de numeración
| Podemos distinguir dos tipos de sistemas de numeración: aditivos y posicionales.
Algunos sistemas de numeración son mixtos, es decir, tienen algo de aditivos y algo de posicionales. (Ej. sist. num. romano y maya). |  |
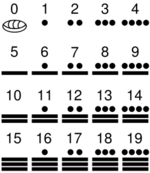
Exposición: Sistemas de numeración Descripción: Sistemas de numeración romano Descripción: Exposición interactiva para repasar el sistema de numeración romano
Actividad: Sistemas de numeración
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
El sistema de numeración decimal
Es nuestro sistema de numeración, nacido en la India en el siglo V y que llegó a Europa por medio de los árabes.
- El sistema de numeración decimal es un sistema de numeración posicional que utiliza 10 símbolos o cifras: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9.
- Al ser un sistema de numeración posicional cada cifra, dependiendo del lugar que ocupe, tiene un valor. Así tenemos diferentes órdenes o categorías de unidades: unidades, decenas, centenas,...
- En este sistema, diez unidades de un orden cualquiera hacen una unidad del orden inmediato superior:
- 1 decena = 10 unidades
- 1 centena = 10 decenas = 100 unidades
- 1 unidad de millar = 10 centenas = 1000 unidades
- 1 decena de millar = 10 unidades de millar = 10,000 unidades
- 1 centena de millar = 10 decenas de millar = 100,000 unidades
- 1 unidad de millón = 10 centenas de millar = 1,000,000 unidades
- 1 decena de millón = 10 unidades de millón = 10,000,000 unidades
- etc.
El número:
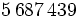
Se lee:
Las cifras ocupan los siguientes órdenes de unidades:
unid. millón |
cent. millar |
dec. millar |
unid. millar |
centenas |
decenas |
unidades |
5 |
6 |
8 |
7 |
4 |
3 |
9 |
5,000,000 unid. |
600,000 unid. |
80,000 unid. |
7,000 unid. |
400 unid. |
30 unid. |
9 unid. |
Ejercicios propuestos
 Ejercicios propuestos: Sistemas de numeración (Pág. 9)
|
