Números complejos: Definición (1ºBach)
De Wikipedia
| Revisión de 08:12 2 oct 2016 Coordinador (Discusión | contribuciones) (→Opuesto y conjugado de un complejo) ← Ir a diferencia anterior |
Revisión de 08:20 2 oct 2016 Coordinador (Discusión | contribuciones) (→Representación gráfica de los números complejos) Ir a siguiente diferencia → |
||
| Línea 190: | Línea 190: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicios: ''El plano complejo'' | ||
| - | |cuerpo= | ||
| {{Video_enlace | {{Video_enlace | ||
| |titulo1= 2 ejercicios | |titulo1= 2 ejercicios | ||
| |duracion=8´00" | |duracion=8´00" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/0301-dos-ejercicios-4#.VCrt9Ra7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/0301-dos-ejercicios-4#.VCrt9Ra7ZV8 | ||
| - | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 249: | Línea 245: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video2 | + | {{Video_enlace |
| - | |titulo1=Fractales... la geometría del caos | + | |titulo1= Fractales... la geometría del caos |
| |duracion=18´ | |duracion=18´ | ||
| - | |url1=http://maralboran.org/web_ma/videos/fractales/fractales.htm | + | |url1=http://www.rtve.es/alacarta/videos/mas-por-menos/aventura-del-saber-serie-mas-menos-fractales-geometria-del-caos/1296590/ |
| - | |titulo2=Acceso por red TIC | + | |url2=http://maralboran.org/web_ma/videos/fractales/fractales.htm |
| - | |url2=http://c0/helvia/aula/archivos/repositorio//0/114/html/index.htm | + | |url3=http://c0/helvia/aula/archivos/repositorio//0/114/html/index.htm |
| - | |sinopsis={{p}} | + | |
| - | El ordenador los ha puesto de moda. Y sin embargo ya eran conocidos a principios de siglo. Nos referimos a los [http://es.wikipedia.org/wiki/Fractal fractales]. Son los objetos matemáticos más atractivos, espectaculares y enigmáticos. A medio camino entre la linea y el plano, entre el plano y el espacio, rompen hasta con el concepto clásico de dimensión. Sus dimensiones no son números enteros, de ahí su extraño nombre. Y sin embargo se pueden obtener mediante simples iteracciones, es decir, repitiendo indefinidamente procedimientos geométricos o funcionales muy simples. Han dado origen a una nueva geometría: la geometría fractal. Una nueva herramienta matemática capaz de arrojar un poco de luz sobre los fenómenos caóticos y de mostrarnos que incluso en el caos es posible encontrar un determinado orden. | + | |
| - | Algunos fractales son representados en el plano complejo, como los [http://es.wikipedia.org/wiki/Conjunto_de_Mandelbrot conjuntos de Mandelbrot] y de [http://es.wikipedia.org/wiki/Conjunto_de_Julia Julia]. | + | |
| - | + | ||
| + | |sinopsis=El ordenador los ha puesto de moda. Y sin embargo ya eran conocidos a principios de siglo. Nos referimos a los [http://es.wikipedia.org/wiki/Fractal fractales]. Son los objetos matemáticos más atractivos, espectaculares y enigmáticos. A medio camino entre la linea y el plano, entre el plano y el espacio, rompen hasta con el concepto clásico de dimensión. Sus dimensiones no son números enteros, de ahí su extraño nombre. Y sin embargo se pueden obtener mediante simples iteracciones, es decir, repitiendo indefinidamente procedimientos geométricos o funcionales muy simples. Han dado origen a una nueva geometría: la geometría fractal. Una nueva herramienta matemática capaz de arrojar un poco de luz sobre los fenómenos caóticos y de mostrarnos que incluso en el caos es posible encontrar un determinado orden. | ||
| + | Algunos fractales son representados en el plano complejo, como los [http://es.wikipedia.org/wiki/Conjunto_de_Mandelbrot conjuntos de Mandelbrot] y de [http://es.wikipedia.org/wiki/Conjunto_de_Julia Julia]. | ||
| }} | }} | ||
| + | |||
| [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | ||
Revisión de 08:20 2 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Necesidad de ampliación del campo numérico
Hay ecuaciones como
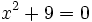
que no tienen solución en el conjunto de los números reales
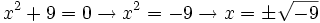 (no existe en
(no existe en  )
)Vamos a definir un nuevo conjunto que amplie al conjunto de los números reales y en el cual estas ecuaciones si tengan solución. Ese conjunto va a ser el conjunto de los números complejos. Para ello habrá que a empezar dando sentido a las raíces de números negativos.
Primero aprendiste a "contar" como un autómata, a modo de mantra: uno, dos, tres, .... Aprendiste a distinguir los correspondientes "símbolos": 1, 2, 3, .... Después llegó el mágico "cero" con su símbolo 0, y con él los números negativos: -1, -2. -3, .... A continuación llegaron las fracciones (y con ellas los números racionales: enteros, decimales exactos y decimales periódicos) y los números irracionales (tienen infinitos decimales y no son periódicos). Por último, llegaron los números reales (unión de los racionales y los irracionales).
Unidad imaginaria
| Desde Al-Jwarizmi (800 DC), precursor del Álgebra, que sólo obtenía las soluciones positivas de las ecuaciones, pasaron más de ocho siglos, hasta que finalmente Descartes en 1637 puso nombre a las raíces cuadradas de números negativos, numeros imaginarios. En 1572, Raffaelle Bombelli, un matemático e ingeniero italiano, las inventó e hizo uso de ellas en sus cálculos en la resolución de ecuaciones. Leibniz decía de los números imaginarios que eran "una especie de anfibios entre el ser y la nada".
Se denomina unidad imaginaria a
El nombre de i le fue dado por Euler en 1777, por imaginario. Y llamó imaginarios a todos los números en cuya expresión aparecía la i. Con esta definición, la ecuación anterior ahora si tiene solución "imaginaria": 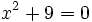
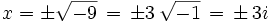 |
Potencias de la unidad imaginaria
|
Actividad: La unidad imaginaria a) Calcula: b) Resuelve la ecuación c) Resuelve la ecuación Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) i^(15) b) solve x^2+9=0 over the reals c) solve x^2+9=0 o solve x^2+9=0 over the complexes |
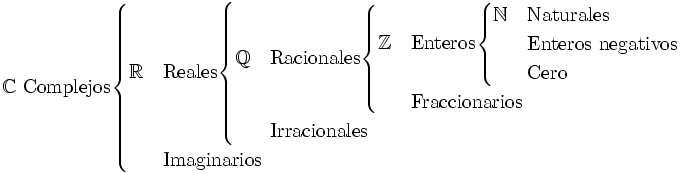
El conjunto de los números complejos
Definimos el conjunto de los números complejos de la siguiente manera:
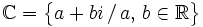
Forma binómica de un número complejo
- La expresión
 se denomina forma binómica de un número complejo.
se denomina forma binómica de un número complejo.
- Si escribimos
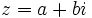 , entonces:
, entonces:
 se le llama parte real o componente real y se denota
se le llama parte real o componente real y se denota 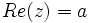 .
.
 se llama parte imaginaria o componente imaginaria y se denota
se llama parte imaginaria o componente imaginaria y se denota 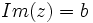 ..
..
- Si
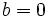 , lo que tenemos es un número real, por tanto
, lo que tenemos es un número real, por tanto 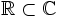 .
.
- Si
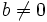 , lo que tenemos no es un número real, se llama número imaginario.
, lo que tenemos no es un número real, se llama número imaginario.
- Si
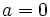 y
y 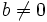 , se le llama número imaginario puro.
, se le llama número imaginario puro.
Igualdad de números complejos
Dos números complejos en forma binómica decimos que son iguales si tienen iguales sus partes reales y sus partes imaginarias.
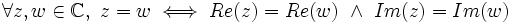
Opuesto y conjugado de un complejo
- Se define el opuesto de un complejo
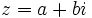 como el número complejo
como el número complejo 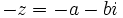 .
.
- Se define el conjugado de un complejo
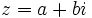 como el número complejo
como el número complejo 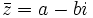 .
.
Proposición
- Cualquier ecuación de segundo grado con coeficientes reales que no tenga solución real tiene dos soluciones imaginarias que son números complejos conjugados.
Videotutorial.
Videotutorial.
Representación gráfica de los números complejos
Videotutorial.
{{{sinopsis}}}
|
Actividad interactiva: Representación gráfica de números complejos
Actividad: Los números complejos se representan mediante vectores. Al extremo del vector se le llama afijo del complejo. Por ejemplo, el afijo del número complejo En el eje horizontal representamos la parte real del número complejo, por eso se le llama eje real . En el eje vertical representamos la parte imaginaria del número complejo, por eso se le llama eje imaginario. Mueve con el ratón el afijo del número complejo de esta escena y podrás ver su representación gráfica por un vector. Si quieres representar un número complejo de forma más exacta, puedes introducir las coordenadas del punto pulsando con el botón derecho sobre él y eligiendo "propiedades" en el menú. Para ver el conjugado y el opuesto marca la casilla correspondiente.
Actividad: En esta escena puedes ver 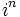 , y su representación gráfica. , y su representación gráfica.
Cambia el valor de n en la parte inferior para ver las sucesivas potencias de |
El ordenador los ha puesto de moda. Y sin embargo ya eran conocidos a principios de siglo. Nos referimos a los fractales. Son los objetos matemáticos más atractivos, espectaculares y enigmáticos. A medio camino entre la linea y el plano, entre el plano y el espacio, rompen hasta con el concepto clásico de dimensión. Sus dimensiones no son números enteros, de ahí su extraño nombre. Y sin embargo se pueden obtener mediante simples iteracciones, es decir, repitiendo indefinidamente procedimientos geométricos o funcionales muy simples. Han dado origen a una nueva geometría: la geometría fractal. Una nueva herramienta matemática capaz de arrojar un poco de luz sobre los fenómenos caóticos y de mostrarnos que incluso en el caos es posible encontrar un determinado orden. Algunos fractales son representados en el plano complejo, como los conjuntos de Mandelbrot y de Julia.
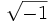 . Se designa por la letra
. Se designa por la letra 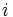 .
.
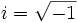

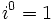
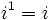
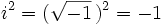
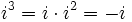
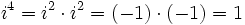
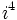 se repiten cíclicamente los valores.
se repiten cíclicamente los valores.
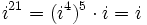 (Al hacer la división entera:
(Al hacer la división entera: 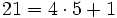 ).
).
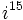 .
.
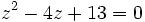
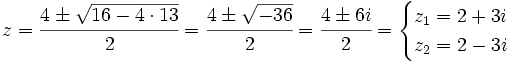
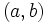 representa las coordenadas de un punto del plano. Diremos que
representa las coordenadas de un punto del plano. Diremos que 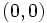 y extremo
y extremo 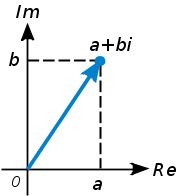

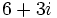 es el punto
es el punto 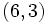 .
.