Distancias en el plano (1ºBach)
De Wikipedia
| Revisión de 17:46 14 oct 2016 Coordinador (Discusión | contribuciones) (→Distancia de un punto a una recta) ← Ir a diferencia anterior |
Revisión de 18:02 14 oct 2016 Coordinador (Discusión | contribuciones) (→Distancia de un punto a una recta) Ir a siguiente diferencia → |
||
| Línea 69: | Línea 69: | ||
| |duracion=7´43" | |duracion=7´43" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/04-distancia-de-un-punto-a-una-recta#.VC7Roha7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/04-distancia-de-un-punto-a-una-recta#.VC7Roha7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis= |
| + | *Cálculo de la distancia de un punto a una recta. | ||
| + | *Ejemplos. | ||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 75: | Línea 77: | ||
| |duracion=9´27" | |duracion=9´27" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0401-ejercicio-11-2#.VC7UHxa7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0401-ejercicio-11-2#.VC7UHxa7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Ejercicio sobre el cálculo de la distancia de un punto a una recta (2 métodos) |
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 81: | Línea 83: | ||
| |duracion=7´33" | |duracion=7´33" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0402-ejercicio-8#.VC7UURa7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0402-ejercicio-8#.VC7UURa7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=En este vídeo calculamos la distancia de un punto a una recta identificada en forma continua. |
| + | Problema típico de examen. No es admisible dejarlo escapar. | ||
| + | |||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 87: | Línea 91: | ||
| |duracion=5´06" | |duracion=5´06" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0403-ejercicio-7#.VC7Ugha7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0403-ejercicio-7#.VC7Ugha7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=En este vídeo calculamos la distancia de un punto a una recta identificada en forma paramétrica. |
| + | Problema típico de examen. No es admisible dejarlo escapar. | ||
| + | |||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 93: | Línea 99: | ||
| |duracion=6´56" | |duracion=6´56" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0404-dos-ejercicios-5#.VC7Uqha7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0404-dos-ejercicios-5#.VC7Uqha7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Dos ejercicios sobre distancia de un punto a una recta en los que una de las coordenadas del punto es un parámetro "k" que hay que averiguar conocido el valor de la distancia. |
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 99: | Línea 105: | ||
| |duracion=4´36" | |duracion=4´36" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0405-ejercicio-2#.VC7U1Ra7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0405-ejercicio-2#.VC7U1Ra7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Hay que determinar la recta que pasa por un punto dado y equidista de dos puntos dados. |
| + | Típico de examen. No puede dejarse escapar. | ||
| + | |||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 105: | Línea 113: | ||
| |duracion=3´29" | |duracion=3´29" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0406-ejercicio#.VC7VEha7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0406-ejercicio#.VC7VEha7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Hay que determinar el punto de una recta dada "r" cuya distancia a la recta dada "s" es conocida. |
| + | Típico de examen. No puede dejarse escapar. | ||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 111: | Línea 120: | ||
| |duracion=4´22" | |duracion=4´22" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0407-ejercicio#.VC7VQBa7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0407-ejercicio#.VC7VQBa7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Dados dos puntos "P" y "Q", hay que determinar la recta que pasa por "P" y está a distancia dada de "Q". |
| + | Típico de examen. No es admisible dejarlo escapar. | ||
| + | |||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 117: | Línea 128: | ||
| |duracion=6´59" | |duracion=6´59" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0408-ejercicio#.VC7VVBa7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0408-ejercicio#.VC7VVBa7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Dados dos vértices de un triángulo equilatero, debemos determinar el tercer vértice. |
| + | Típico de examen. No puede dejarse escapar. | ||
| + | |||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 123: | Línea 136: | ||
| |duracion=10´07" | |duracion=10´07" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0409-ejercicio#.VC7V0Ba7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0409-ejercicio#.VC7V0Ba7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Problema típico de examen sobre triángulos uno de cuyos vértices tiene una coordenada desconocida que hay que determinar, conocida el área. No es admisible dejarlo escapar. |
| + | |||
| + | La solución que damos sirve para ilustrar el uso de "ventanas", que facilitan la tarea a tu profe y le hacen feliz. | ||
| + | |||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 129: | Línea 145: | ||
| |duracion=6´27" | |duracion=6´27" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0410-ejercicio#.VC7V7ha7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0410-ejercicio#.VC7V7ha7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Determinar un punto de una recta que determina con otros dos puntos dados un triángulo de área dada. |
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| Línea 135: | Línea 151: | ||
| |duracion=7´18" | |duracion=7´18" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0411-ejercicio#.VC7WGha7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/09-la-recta-en-el-plano/0411-ejercicio#.VC7WGha7ZV8 | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=Nos dan tres vértices consecutivos de un paralelogramo y debemos determinar el cuarto vértice y el área del paralelogramo. |
| + | Otro ejemplo de uso de "ventanas"..... esfuérzate en aprender a emplearlas. | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 18:02 14 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 203)
Distancia ente dos puntos
La distancia entre dos puntos 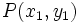 y
y 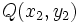 es igual al módulo del vector
es igual al módulo del vector 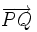 :
:
|
|
|
Actividad Interactiva: Distancia entre dos puntos
Actividad 1: En esta escena vamos a hallar la distancia entre los puntos
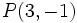 y y 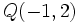 . .Actividad: 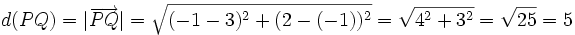
Ejercicio: Calcula la distancia entre los puntos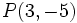 y y 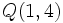 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
Distancia de un punto a una recta
Proposición
- La distancia del punto
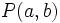 a la recta
a la recta 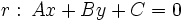 es:
es:
|
|
Ejercicio resuelto: Distancias en el plano
Halla el área del triángulo de vértices A(0,0), B(6,5) y C(2,5).
Tomando como base del triángulo el lado BC, tendremos que calcular d(B,C) y d(A, BC) para hallar las medidas de la base y de la altura.
Solución: Área=10 u2.- Cálculo de la distancia de un punto a una recta.
- Ejemplos.
Ejercicio sobre el cálculo de la distancia de un punto a una recta (2 métodos)
En este vídeo calculamos la distancia de un punto a una recta identificada en forma continua. Problema típico de examen. No es admisible dejarlo escapar.
En este vídeo calculamos la distancia de un punto a una recta identificada en forma paramétrica. Problema típico de examen. No es admisible dejarlo escapar.
Dos ejercicios sobre distancia de un punto a una recta en los que una de las coordenadas del punto es un parámetro "k" que hay que averiguar conocido el valor de la distancia.
Hay que determinar la recta que pasa por un punto dado y equidista de dos puntos dados. Típico de examen. No puede dejarse escapar.
Hay que determinar el punto de una recta dada "r" cuya distancia a la recta dada "s" es conocida. Típico de examen. No puede dejarse escapar.
Dados dos puntos "P" y "Q", hay que determinar la recta que pasa por "P" y está a distancia dada de "Q". Típico de examen. No es admisible dejarlo escapar.
Dados dos vértices de un triángulo equilatero, debemos determinar el tercer vértice. Típico de examen. No puede dejarse escapar.
Problema típico de examen sobre triángulos uno de cuyos vértices tiene una coordenada desconocida que hay que determinar, conocida el área. No es admisible dejarlo escapar.
La solución que damos sirve para ilustrar el uso de "ventanas", que facilitan la tarea a tu profe y le hacen feliz.
Determinar un punto de una recta que determina con otros dos puntos dados un triángulo de área dada.
Nos dan tres vértices consecutivos de un paralelogramo y debemos determinar el cuarto vértice y el área del paralelogramo. Otro ejemplo de uso de "ventanas"..... esfuérzate en aprender a emplearlas.
|
Actividad Interactiva: Distancia de un punto a una recta
Actividad 1: En esta escena vamos a hallar la distancia del punto
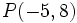 a la recta a la recta 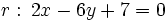 . .Actividad: 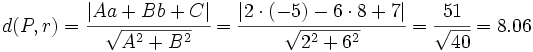
Ejercicio: Calcula la distancia del punto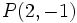 a la recta a la recta 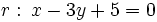 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
Distancia entre dos rectas
Videotutorial
Videotutorial
Bisectrices del ángulo entre dos rectas
Videotutorial
Videotutorial
Videotutorial
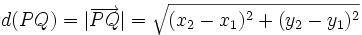
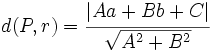
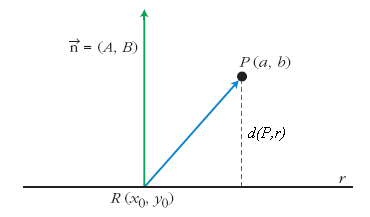
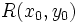 un punto de la recta.
un punto de la recta.
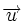
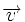
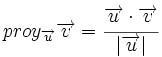
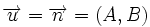
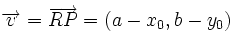
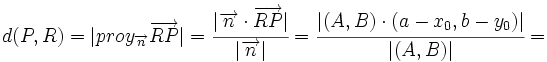
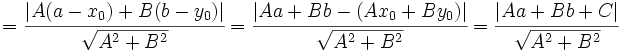
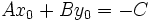 , por ser
, por ser 
