Plantilla:Mediatriz de un segmento
De Wikipedia
| Revisión de 17:50 18 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:31 18 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema|titulo=Proposición|enunciado=La mediatriz de un segmento es una recta perpendicular al segmento que pasa por su punto medio. | + | {{Teorema|titulo=Propiedad|enunciado=La mediatriz de un segmento es una recta perpendicular al segmento que pasa por su punto medio. |
| |demo=Para hallar la ecuación de la mediatriz AB, siendo <math>A=(x_a,y_a)\;</math> y <math>B=(x_b,y_b)\;</math> tenemos que hallar la ecuación del lugar geométrico | |demo=Para hallar la ecuación de la mediatriz AB, siendo <math>A=(x_a,y_a)\;</math> y <math>B=(x_b,y_b)\;</math> tenemos que hallar la ecuación del lugar geométrico | ||
| {{p}} | {{p}} | ||
Revisión de 18:31 18 nov 2016
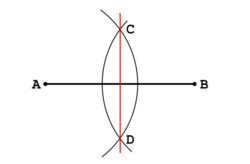
La mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan de sus extremos. Así, dado el segmento
En esta escena podrás ver como construye la mediatriz de un segmento. |
Propiedad
La mediatriz de un segmento es una recta perpendicular al segmento que pasa por su punto medio.
Para hallar la ecuación de la mediatriz AB, siendo 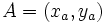 y
y 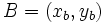 tenemos que hallar la ecuación del lugar geométrico
tenemos que hallar la ecuación del lugar geométrico
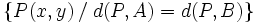
Para ello escribiremos la fórmula de la distancia entre dos puntos:
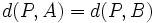
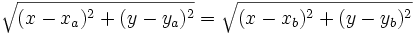
Elevando ambos miembros al cuadrado, desarrollando los cuadrados de los binomios y simplificando, comprueba que queda la ecuación:
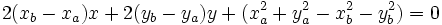
Por tanto, la ecuación de la mediatriz del segmento AB es la ecuación de una recta.
Faltaría ver que es perpendicular al segmento y que pasa por su punto medio.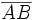 , su mediatriz está formada por los puntos
, su mediatriz está formada por los puntos  del siguiente conjunto:
del siguiente conjunto: