Las cónicas (1ºBach)
De Wikipedia
| Revisión de 16:20 19 oct 2016 Coordinador (Discusión | contribuciones) (→Ecuaciones de las cónicas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Las órbitas de los planetas y de los cometas) |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Secciones cónicas== | ==Secciones cónicas== | ||
| - | {{Tabla75|celda2=[[Imagen:Cono y secciones.jpg|220px|center]] | + | {{secciones cónicas}} |
| - | |celda1= | + | |
| - | {{Caja_Amarilla|texto=Se denomina '''sección cónica''' a la curva intersección de un cono con un plano que no pasa por su vértice. | + | |
| - | + | ||
| - | Según como corte el plano al cono tendremos (ver figura): | + | |
| - | + | ||
| - | *'''Hipérbola:''' el plano forma con la base un ángulo mayor que el que forma la generatriz. | + | |
| - | *'''Parábola:''' el plano es paralelo a la generatriz. | + | |
| - | *'''Elipse:''' el plano forma con la base un ángulo menor que el que forma la generatriz. | + | |
| - | *'''Circunferencia:''' el plano es paralelo a la base. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | La primera definición de sección cónica aparece en Grecia, cerca del año 350, donde las definieron como secciones de un cono circular recto. Los nombres de hipérbola, parábola y elipse se deben a [[Apolonio |Apolonio de Pérgamo]]. | ||
| - | A continuación vamos a ver definir las secciones cónicas como lugares geométricos de puntos del plano. | ||
| - | }} | ||
| - | {{p}} | ||
| ==Las cónicas como lugares geométricos== | ==Las cónicas como lugares geométricos== | ||
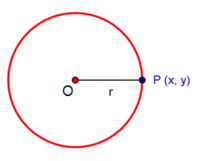
| ===Circunferencia=== | ===Circunferencia=== | ||
| - | {{Tabla75|celda2=[[Imagen:trazado_circunferencia.png|right|210px|center]]|celda1= | + | {{circunferencia}} |
| - | {{Caja_Amarilla|texto= La '''circunferencia''' de '''centro''' <math>O\,</math> y '''radio''' <math>r\,</math>, es el lugar geométrico de los puntos <math>P\,</math>, del plano, cuya distancia al centro es <math>r\,</math>. | + | |
| - | + | ||
| - | {{Caja|contenido=<math>\big \{P(x,y) \, / \; d(P,O)=r \big \}</math>}} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver como se dibuja una circunferencia. | + | |
| - | |enlace=[https://ggbm.at/MUVfrgJr Trazado de la circunferencia] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Par más detalles consulta el tema de la [[La circunferencia (1ºBach) |circunferencia]]. | Par más detalles consulta el tema de la [[La circunferencia (1ºBach) |circunferencia]]. | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Elipse=== | ===Elipse=== | ||
| - | {{Tabla75|celda2=[[Imagen:trazado_elipse.jpg|right|210px|center]]|celda1= | + | {{elipse}} |
| - | {{Caja_Amarilla|texto=Dados dos puntos <math>F\,</math> y <math>F'\,</math> llamados '''focos''', y una distancia <math>k\,</math>, llamada '''constante de la elipse''' (<math>k > d(F,F')\,</math>), se llama '''elipse''' al lugar geométrico de los puntos <math>P\,</math> del plano cuya suma de distancias a los focos es igual a <math>k\,</math>: | + | |
| - | + | ||
| - | {{Caja|contenido=<math>\big \{P(x,y) \, / \; d(P,F)+d(P,F')=k \big \}</math>}} | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver como construye una elipse. | + | |
| - | |enlace=[https://ggbm.at/f462a5R2 Trazado de la elipse] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Par más detalles consulta el tema de la [[La elipse (1ºBach) |elipse]]. | Par más detalles consulta el tema de la [[La elipse (1ºBach) |elipse]]. | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| ===Hipérbola=== | ===Hipérbola=== | ||
| - | {{Tabla75|celda2=[[Imagen:hiperbola.gif|right|210px|center]]|celda1= | + | {{hipérbola}} |
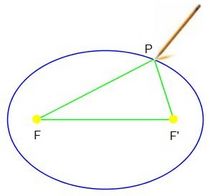
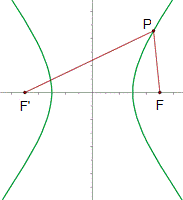
| - | {{Caja_Amarilla|texto=Dados dos puntos <math>F\,</math> y <math>F'\,</math> llamados '''focos''', y una distancia <math>k\,</math>, llamada '''constante de la hipérbola''' (<math>k < d(F,F')\,</math>), se llama '''hipérbola''' al lugar geométrico de los puntos <math>P\,</math> del plano cuya diferencia de distancias a los focos es, en valor absoluto, igual a <math>k\,</math>: | + | |
| - | + | ||
| - | {{Caja|contenido=<math>\big \{P(x,y) \, / \; |d(P,F)-d(P,F')|=k \big \}</math>}} | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver como construye una hipérbola. | + | |
| - | |enlace=[https://ggbm.at/ukt4c5TW Trazado de la hipérbola] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Par más detalles consulta el tema de la [[La hipérbola (1ºBach) |hipérbola]]. | Par más detalles consulta el tema de la [[La hipérbola (1ºBach) |hipérbola]]. | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Parábola=== | ===Parábola=== | ||
| - | {{Tabla75|celda2=<center>[[Imagen:parabola.jpg|right|210px|center]]<br><math>d(P_i,F)=d(P_i,Q_i)\;</math></center>|celda1= | + | {{parabola}} |
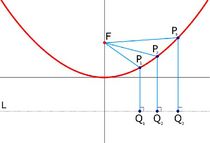
| - | {{Caja_Amarilla|texto=Dados un punto <math>F\,</math> llamado '''foco''', y una recta <math>d\,</math>, llamada '''directriz''', se llama '''parábola''' al lugar geométrico de los puntos <math>P\,</math> del plano que equidistán del foco y de la directriz: | + | |
| - | + | ||
| - | {{Caja|contenido=<math>\big \{P(x,y) \, / \; d(P,F)=d(P,d) \big \}</math>}} | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver como construye una parábola. | + | |
| - | |enlace=[https://ggbm.at/e4XQQ2Ss Trazado de la parábola] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Par más detalles consulta el tema de la [[La parábola (1ºBach) |parábola]]. | Par más detalles consulta el tema de la [[La parábola (1ºBach) |parábola]]. | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| ==Ecuaciones de las cónicas== | ==Ecuaciones de las cónicas== | ||
| - | {{Caja_Amarilla|texto= | + | {{Teorema_sin_demo|titulo=Proposición|enunciado= |
| A partir de las ecuaciones de los lugares geométricos anteriormente vistos, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma: | A partir de las ecuaciones de los lugares geométricos anteriormente vistos, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma: | ||
| Línea 106: | Línea 51: | ||
| ==Excentricidad de una cónica== | ==Excentricidad de una cónica== | ||
| {{Tabla75|celda1= | {{Tabla75|celda1= | ||
| - | {{Caja_Amarilla|texto=La '''excentricidad''' <math>e\,</math> de una cónica es un parámetro que determina el grado de desviación de la cónica con respecto a una circunferencia.}} | + | {{Caja_Amarilla|texto=La '''excentricidad''', <math>e\,</math>, de una cónica es un parámetro que determina el grado de desviación de la cónica con respecto a una circunferencia.}} |
| {{p}} | {{p}} | ||
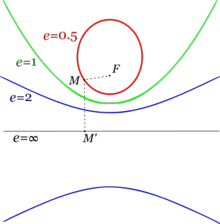
| '''Valores de la excentricidad de las cónicas:''' | '''Valores de la excentricidad de las cónicas:''' | ||
| Línea 115: | Línea 60: | ||
| *'''Hipérbola:''' <math>e>1\,</math>. | *'''Hipérbola:''' <math>e>1\,</math>. | ||
| }} | }} | ||
| + | {{p}} | ||
| + | El por qué de estos valores se estudiará en el apartado correspondiente a cada cónica. | ||
| |celda2= | |celda2= | ||
| {{b4}}[[Imagen:Excentricidad.png|220px]] | {{b4}}[[Imagen:Excentricidad.png|220px]] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | '''Las órbitas de los planetas y de los cometas:''' | + | ===Las órbitas de los planetas y de los cometas=== |
| - | {{Tabla75|celda2=[[Imagen:orbitascometas.png|200px|center]] | + | {{orbitas planetas}} |
| - | |celda1={{p}} | + | |
| - | *Los planetas tienen órbitas elípticas, siendo uno de sus focos el Sol, con excentricidad casi nula (muy parecidas a una circunferencia). La excentricidad de la tierra es 0,017. | + | |
| - | *Las órbitas de los cometas son elípticas, muy excéntricas (muy alargadas), algunas incluso son parabólicas e hiperbólicas. | + | |
| - | **Los cometas de órbitas parabólicas y más los de órbitas hiperbólicas, debemos considerarlos como astros sólo visibles una vez, a menos que durante su trayecto por el interior del sistema Solar pasen por la proximidad de un astro de gran masa, como Júpiter, y que, por efecto de su gran fuerza atractiva, o capture, transformando su primitiva órbita abierta en una elipse y, por lo tanto, obligándole a dar vueltas alrededor del Sol. | + | |
| - | **La sección cónica que exhibe una órbita depende de su energía total. Si la energía total del sistema es negativa, entonces la órbita es ligada y asumirá una conformación elíptica. Ahora, si es exactamente igual a cero, la órbita será desligada y tendrá una forma parabólica. Si la energía es positiva, la órbita será también desligada y seguirá una hipérbola. | + | |
| - | }} | + | |
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Secciones cónicas
Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. Según como corte el plano al cono tendremos (ver figura):
La primera definición de sección cónica aparece en Grecia, cerca del año 350, donde las definieron como secciones de un cono circular recto. Los nombres de hipérbola, parábola y elipse se deben a Apolonio de Pérgamo. A continuación vamos a ver definir las secciones cónicas como lugares geométricos de puntos del plano. | 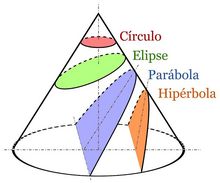 Secciones cónicas: Los nombres de hipérbola, parábola y elipse se deben a Apolonio de Pérgamo. |
Las cónicas como lugares geométricos
Circunferencia
La circunferencia de centro
En esta escena podrás ver como se dibuja una circunferencia. |
Par más detalles consulta el tema de la circunferencia.
Elipse
Dados dos puntos
En esta escena podrás ver como construye una elipse. |
Par más detalles consulta el tema de la elipse.
Hipérbola
Dados dos puntos
En esta escena podrás ver como construye una hipérbola. |
Par más detalles consulta el tema de la hipérbola.
Parábola
Dados un punto
En esta escena podrás ver como construye una parábola. |
Par más detalles consulta el tema de la parábola.
Ecuaciones de las cónicas
Proposición
A partir de las ecuaciones de los lugares geométricos anteriormente vistos, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma:
|
|
en la que, en función de los valores de los parámetros, se tendrá:
- Hipérbola: si
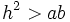
- Parábola: si
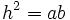
- Elipse: si
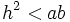
- Circunferencia: si
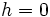 y
y 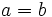
Excentricidad de una cónica
Las órbitas de los planetas y de los cometas
|
Los planetas tienen órbitas elípticas, siendo uno de sus focos el Sol, con excentricidad casi nula (muy parecidas a una circunferencia). La excentricidad de la tierra es 0,017. Las órbitas de los cometas son elípticas, muy excéntricas (muy alargadas), algunas incluso son parabólicas e hiperbólicas. Los cometas de órbitas parabólicas y más los de órbitas hiperbólicas, debemos considerarlos como astros sólo visibles una vez, a menos que durante su trayecto por el interior del sistema Solar pasen por la proximidad de un astro de gran masa, como Júpiter, y que, por efecto de su gran fuerza atractiva, o capture, transformando su primitiva órbita abierta en una elipse y, por lo tanto, obligándole a dar vueltas alrededor del Sol. La sección cónica que exhibe una órbita depende de su energía total. Si la energía total del sistema es negativa, entonces la órbita es ligada y asumirá una conformación elíptica. Ahora, si es exactamente igual a cero, la órbita será desligada y tendrá una forma parabólica. Si la energía es positiva, la órbita será también desligada y seguirá una hipérbola. |
 y radio
y radio  , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos  , del plano, cuya distancia al centro es
, del plano, cuya distancia al centro es 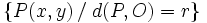
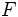 y
y 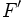 llamados focos, y una distancia
llamados focos, y una distancia  , llamada constante de la elipse (
, llamada constante de la elipse (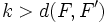 ), se llama elipse al lugar geométrico de los puntos
), se llama elipse al lugar geométrico de los puntos 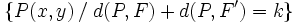
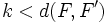 ), se llama hipérbola al lugar geométrico de los puntos
), se llama hipérbola al lugar geométrico de los puntos 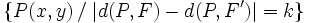
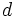 , llamada directriz, se llama parábola al lugar geométrico de los puntos
, llamada directriz, se llama parábola al lugar geométrico de los puntos 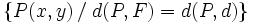
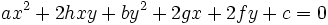
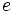 , de una cónica es un parámetro que determina el grado de desviación de la cónica con respecto a una circunferencia.
, de una cónica es un parámetro que determina el grado de desviación de la cónica con respecto a una circunferencia.
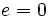 .
.
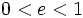 .
.
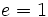 .
.
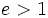 .
.