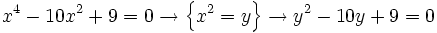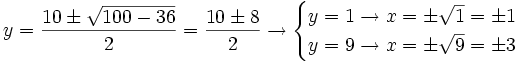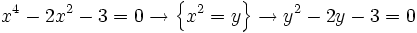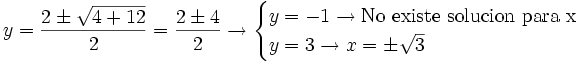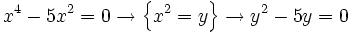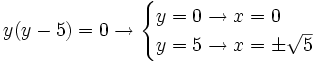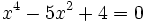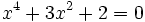Plantilla:Ecuaciones bicuadradas
De Wikipedia
| Revisión de 09:37 20 abr 2017 Coordinador (Discusión | contribuciones) (→Resolución de la ecuación bicuadrada) ← Ir a diferencia anterior |
Revisión de 09:39 20 abr 2017 Coordinador (Discusión | contribuciones) (→Resolución de la ecuación bicuadrada) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| |titulo1=Ecuaciones bicuadradas | |titulo1=Ecuaciones bicuadradas | ||
| |duracion=5'33" | |duracion=5'33" | ||
| - | |sinopsis=Ejemplo de resolución de una ecuación bicuadrada. | + | |sinopsis=Ejemplo de resolución de una ecuación bicuadrada y de factorización del polinomio. |
| |url1=http://www.unicoos.com/video/matematicas/3-eso/ecuaciones/ecuaciones-bicuadradas/ecuacion-bicuadrada | |url1=http://www.unicoos.com/video/matematicas/3-eso/ecuaciones/ecuaciones-bicuadradas/ecuacion-bicuadrada | ||
| }} | }} | ||
Revisión de 09:39 20 abr 2017
Las ecuaciones bicuadradas son ecuaciones de cuarto grado que no tienen terminos de grado impar, es decir son de la forma
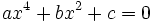
Resolución de la ecuación bicuadrada
Resolución de la ecuación bicuadrada
El método para resolver una ecuación bicuadrada
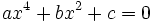
consiste en hacer el cambio de variable 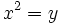 . Entonces, nos quedará la siguiente ecuación de segundo grado en "y".
. Entonces, nos quedará la siguiente ecuación de segundo grado en "y".
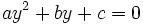
Una vez resuelta esta ecuación en "y", tenemos que averiguar el valor de la "x". Para ello desharemos el cambio de variable, haciendo 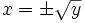 . En consecuencia, las soluciones
. En consecuencia, las soluciones 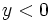 , las rechazaremos, ya que no darán solución para la
, las rechazaremos, ya que no darán solución para la 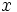 , quedándonos sólo con las soluciones de
, quedándonos sólo con las soluciones de 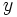 no negativas, cada una de las cuales dará dos soluciones para la
no negativas, cada una de las cuales dará dos soluciones para la 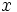 .
.
En consecuencia, una ecuación bicuadrada tendrá, como máximo, cuatro soluciones reales.
Ejemplo de resolución de una ecuación bicuadrada y de factorización del polinomio.
- Método de resolución de ecuaciones bicuadradas.
- Ejemplos.
Ejercicios resueltos: Ecuaciones bicuadradas
Resuelve las ecuaciones:
- a)
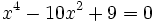
- b)
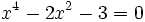
- c)
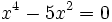
a)
- Soluciones:
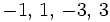
b)
- Soluciones:
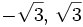
c)
- Soluciones:
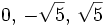
Resolución de las siguientes ecuaciones:
- a) x4 + 3x2 − 4 = 0
- b) x4 − 9x2 = 0
- c) x4 − 9 = 0
- d) x4 + 5 = 0
- e) x6 − 9x3 + 8 = 0