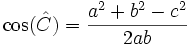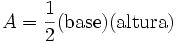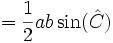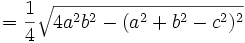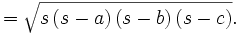Plantilla:Area triangulo
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:54 16 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 01:51 7 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | |||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| {{Tabla3 | {{Tabla3 | ||
| Línea 15: | Línea 14: | ||
| :<math>c \ , d\;</math>: lados. | :<math>c \ , d\;</math>: lados. | ||
| * '''Nota:''' | * '''Nota:''' | ||
| - | :Un triángulo es la mitad de un paralelogramo. | + | :Un [[Triángulos |triángulo]] es la mitad de un paralelogramo. |
| }} | }} | ||
| }} | }} | ||
| Línea 26: | Línea 25: | ||
| {{teorema | {{teorema | ||
| |titulo=Fórmula de Herón | |titulo=Fórmula de Herón | ||
| - | |enunciado=La superficie de un triángulo de lados <math>a\;</math>, <math>b\;</math>, <math>c\;</math> viene dada por: | + | |enunciado=La superficie de un [[Triángulos |triángulo]] de lados <math>a\;</math>, <math>b\;</math>, <math>c\;</math> viene dada por: |
| <center><math>A = \sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}\,</math></center> | <center><math>A = \sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}\,</math></center> | ||
Revisión de 01:51 7 may 2017
|
|
En esta escena podrás deducir la fórmula del área del triángulo.
Fórmula de Herón
Demostración:
Nota: El nivel de esta demostración corresponde a 1º de Bachillerato.
Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente.
Supongamos un triángulo de lados  ,
,  ,
,  , cuyos ángulos opuestos a cada uno de esos lados son
, cuyos ángulos opuestos a cada uno de esos lados son 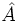 ,
, 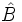 ,
, 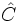 .
.
Por el teorema del coseno, tenemos que:
Por la relación fundamental de la trigonometría, tenemos que:
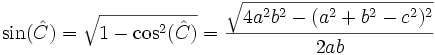 .
.
La altura de un triángulo de base  tiene una longitud
tiene una longitud 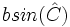 , por tanto siguiendo con la demostración
, por tanto siguiendo con la demostración
En esta escena podrás calcular el área de un triángulo mediante la fórmula de Herón.
|
Actividad: El triángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|

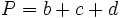
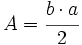
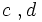 : lados.
: lados.
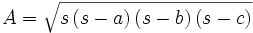
 es el semiperímetro:
es el semiperímetro: 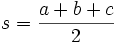 .
.