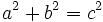Triángulos
De Wikipedia
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Triángulo
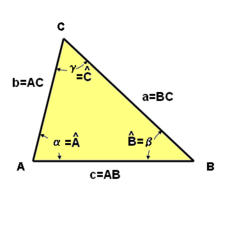
Un triángulo es un polígono de tres lados. Nomenclatura:
| 
|
Propiedades
Todo triángulo cumple las siguientes propiedades:
- Sus tres ángulos suman 180º.
- La longitud de cada lado es menor que la suma de los otros dos.
- Es rígido, de hecho, es el único polígono indeformable.
- Si
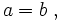 entonces
entonces 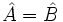 . Y si
. Y si 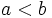 , entonces
, entonces 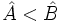 .
.
1. Los tres ángulos de un triángulo suman 180º.
Podrás ver la demostración en el siguiente video:
Demostración de que la suma de los ángulos de un triángulo es un ángulo llano (180º).
Para comprobar esta propiedad vamos a hacer uso de la siguiente escena. En ella, A es un punto fijo, B puede moverse horizontalmente y C libremente: esto permite dibujar cualquier triángulo. La recta que pasa por C es paralela al lado AB con lo cual los ángulos verdes son iguales por ser alternos internos, y los rojos también, por la misma razón. Si sumamos los tres ángulos en el vértice C, obtenemos siempre un ángulo llano.
2. La longitud de cada lado es menor que la suma de los otros dos.
En la siguiente escena puedes comprobar esta propiedad. Mueve los vértices para cambiar la forma del triángulo.
3. Es rígido, de hecho, el triángulo es el único polígono indeformable.
Observa la escena, arrastra los vértices y comprueba que:
a) Con tres varillas iguales podemos formar un triángulo, que no se deforma.
b) Con cuatro varillas iguales, el cuadrilátero que se forma, puede deformarse, no es rígido.
Esta propiedad tiene muchas aplicaciones en la construcción. Observa torres de la luz, estructuras metálicas de puentes,... la forma externa puede ser variada, pero llevan diagonales internas que dividen su estructura en triángulos.
4. Si 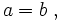 entonces
entonces 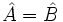 . Y si
. Y si 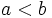 , entonces
, entonces 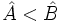
Demostración de Teoremas Fundamentales de los Triángulos
Triángulo: Definición, elementos y propiedades
Convenio y notación para nombrar los lados y los ángulos de un triángulo.
2 ejemplos de aplicación de la propiedad nº 1 de los triángulos, que dice:
"La suma de los ángulos interiores de un triángulo es 180º"
Propiedades de los ángulos interiores y exteriores de un triángulo.
Propiedades de los ángulos y lados de un triángulo.
Suma de los ángulos de un triángulo. Casos particulares.
Propiedades de los lados y ángulos de un triángulo. Ejemplos.
6 teoremas sobre las propiedades de los lados y ángulos de un triángulo.
Lista de vídeos de ejercicios sobre las propiedades de los triángulos.
El triángulo es el único polígono rígido.
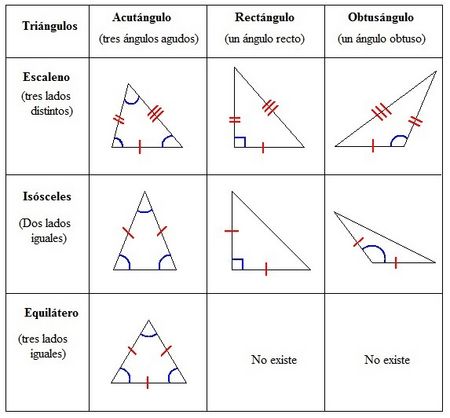
Clasificación de los triángulos
Según sus lados:
Según sus ángulos:
Triángulos. Suma de sus ángulos. Clasificación según sus lados y sus ángulos. Clasificación de los triángulos según sus lados y sus ángulos. Clasificación de los triángulos según sus lados y sus ángulos. Clasificación de los triángulos según sus lados y sus ángulos. Actividades en las que podrás aprender los elementos de un triángulo y a clasificar estos atendiendo a sus lados y a sus ángulos. Actividad en la qué podrás comprobar lo que sabes sobre la clasificación de los triángulos atendiendo a sus lados o a sus ángulos. |
Igualdad de triángulos
Dos triángulo son iguales (congruentes) si tienen sus lados y sus ángulos iguales.
Para que dos triángulos sean iguales basta con que se verifique una de las siguientes condiciones:
Criterios de congruencia de triángulos
- Dos triángulos son iguales si tienen los tres lados iguales (LLL).
- Dos triángulos son iguales si tienen dos lados iguales y también es igual el ángulo comprendido entre ellos (LAL).
- Dos triángulos son iguales si tienen un lado igual y son iguales sus ángulos contiguos (ALA).
Criterios que permiten determinar cuando dos triángulos son iguales (congruentes).
- Criterio de congruencia de triángulos LLL.
- Ejercicio de aplicación nº1.
- Criterio de congruencia de triángulos LLL.
- Ejercicio de aplicación nº2.
- Criterio de congruencia de triángulos LAL.
- Ejercicio de aplicación nº1.
- Criterio de congruencia de triángulos LAL.
- Ejercicio de aplicación nº2.
- Criterio de congruencia de triángulos ALA.
- Ejercicio de aplicación nº1.
- Criterio de congruencia de triángulos ALA .
- Ejercicio de aplicación nº2.
- Cuarto criterio (caso especial) de congruencia de triángulos.
- Ejercicio de aplicación.
En este video, apoyándonos en los criterios de congruencia de triángulos, se comprobará la siguiente propiedad de la mediatriz de un segmento:
"Todo punto que se encuentre sobre la mediatriz de un segmento, equidista de los extremos del segmento"
Tras ello se verá un ejercicio de aplicación de esa propiedad.
En este video, apoyándonos en los criterios de congruencia de triángulos, se comprobará la siguiente propiedad de la bisectriz de un ángulo:
"Cualquier punto que se encuentra en la bisectriz de un ángulo, equidista de los lados del ángulo."
Tras ello se verá un ejercicio de aplicación de esa propiedad.
Construcción de triángulos
Basándonos en lo anterior podemos dar el siguiente resultado:
Procedimiento
Es posible construir un triángulo si se da alguna de las siguientes situaciones:
- a) Se conocen los tres lados (LLL).
- b) Se conocen dos lados y el ángulo comprendido entre ellos (LAL).
- c) Se conocen un lado y sus dos ángulos contiguos (ALA).
a) Construcción de un triángulo conociendo los tres lados (LLL):
Recuerda que para poder realizar la construcción la medida de cada lado ha de ser menor que la suma de los otros dos.
- Se representa un segmento de medida igual al primer lado.
- Desde cada extremo del primer lado se traza una circunferencia de radio el valor del segundo y tercer lado.
- El triangulo tiene por vértices los extremos del primer segmento y una de las intersecciones de las circunferencias.
b) Construcción de un triángulo, conocidos dos lados y el ángulo comprendido entre ellos (LAL):
- Se representa uno de los segmentos.
- Se traza el ángulo que forman los lados.
- Se lleva el segundo lado conocido sobre el lado del ángulo.
- Basta con unir los extremos de los dos lados para construir el triángulo.
c) Construcción de un triángulo conocido un lado y sus dos ángulos contiguos (ALA):
Recuerda que la suma de los dos ángulos conocidos ha de ser menor de 180º.
- Se construye el lado conocido.
- Desde cada uno de los extremos del lado se trazan los ángulos dados.
- La intersección de los lados de los ángulos es el tercer vértice del triángulo.
Construcción de un triángulo conociendo los tres lados (LLL), con regla y compás.
Construcción de un triángulo, conocidos dos lados y el ángulo comprendido entre ellos (LAL), con regla y compás.
Construcción de un triángulo conocido un lado y sus dos ángulos contiguos (ALA), con regla y compás.
Construcción de un triángulo equilátero conocido el lado, con regla y compás.
Construcción de un triángulo conociendo los tres lados (LLL), con regla y compás.
Construcción de un triángulo conociendo los dos lados y el ángulo comprendido entre ellos (LAL) , con regla y compás.
Actividades en las que podrás aprender a construir triángulos a partir de sus lados y de sus ángulos, en los casos vistos anteriormente: LLL, ALA y LAL.
Aprende a construir triángulos. Ejercicios resueltos.
Rectas y puntos notables en un triángulo
El video y las actividades que tienes a continuación resumen lo que vamos a ver en este apartado.
Construcción de triángulos. Elementos notables y su construcción.
En este video vamos a estudiar las rectas y puntos notables de un triángulo:
- Rectas: bisectriz, mediana, mediatriz y altura.
- Puntos: incentro, baricentro, circuncentro y ortocentro.
Actividades en las que podrás aprender cuáles son los puntos y rectas notables de un triángulo.
Actividades en las que podrás aprender cuáles son los puntos y rectas notables de un triángulo.
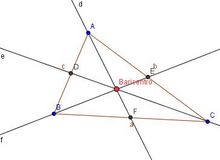
Medianas y baricentro
Puntos y rectas notables de un triángulo: medianas y baricentro. Medianas y baricentro de un triángulo. Propiedad del baricentro. Construcción con regla y compás de las medianas y del baricentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su baricentro y sus medianas. |
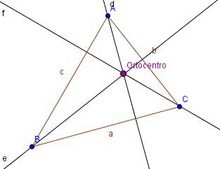
Alturas y ortocentro
Puntos y rectas notables de un triángulo: alturas y ortocentro. Alturas y ortocentro de un triángulo según sea rectángulo, acutángulo u obtusángulo. Construcción con regla y compás de las alturas y del ortocentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su ortocentro y sus alturas. |
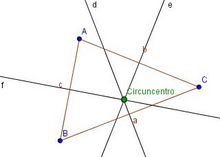
Mediatrices y circuncentro
Puntos y rectas notables de un triángulo: mediatrices y circuncentro. Construcción con regla y compás de las mediatrices y del circuncentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su circuncentro y sus mediatrices. |
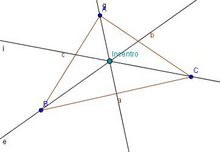
Bisectrices e incentro
Puntos y rectas notables de un triángulo: bisectrices e incentro. Construcción con rtegla y compás de las bisectrices y del incentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su incentro y sus bisectrices. |
Recta de Euler
|
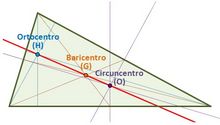
La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo. Construcción con regla y compás del ortocentro, baricentro y circuncentro y de la recta de Euler. En esta escena podrás ver e interactuar con un triángulo y ver la recta de Euler. |
Triángulos rectángulos
Una breve explicación sobre lo que sucede con los ángulos internos de los triángulos. | 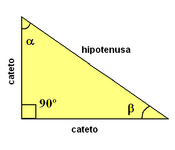
|
La siguiente escena muestra como construir un triángulo rectángulo usando una circunferencia.
Consiste en inscribirlo en una circunferencia cuyo diámetro coincida con la hipotenusa. Esto es así por una propiedad de los ángulos inscritos en una circunferencia.
Mueve el punto C y comprueba que el triángulo inscrito de esta forma siempre es rectángulo.
Teorema de Pitágoras
Teorema de Pitágoras
| En un triángulo rectángulo la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos:
| 
|
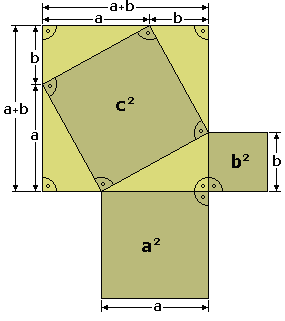
| Fíjate en la figura de la derecha y observa como el cuadrado grande, de lado a + b, puede descomponerse en un cuadrado de lado c y 4 triángulos rectángulos, como el de partida, de catetos a y b e hipotenusa c.
La superficie del cuadrado grande de lado a + b es: 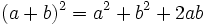 La superficie de los cuatro triángulos rectángulos es : 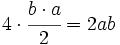 Restando el área del cuadrado grande de lado a + b menos las areas de los 4 triángulos rectángulos, se obtiene el área del cuadrado de lado c: 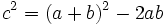 Desarrollando el cuadrado del binomio: 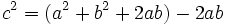 De donde obtenemos, simplificando: 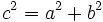 |
Teorema de Pitágoras:
Teorema de Pitágoras. Ejemplos y ejercicios.
Teorema de Pitágoras. Ejemplos y ejercicios.
Teorema de Pitágoras. Ejemplos.
Teorema de Pitágoras y recíproco. Ejemplo.
Demostraciones:
Demostración del teorema de Pitágoras mediante una construcción geométrica, con ejemplos previos de casos particulares.
La misma demostración del teorema de Pitágoras mediante una construcción geométrica, sin ejemplos previos.
Otra demostración basada en el teorema de la altura y el teorema del cateto.
Consta de tres partes:
Demostración del teorema de de la altura.
Demostración del teorema del cateto.
Demostración del teorema de Pitágoras.
Otros videos:
Pitágoras. El teorema de Pitágoras. Demostraciones.
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Pero las Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.
Esta unidad didáctica presenta varias demostraciones del teorema de Pitágoras.
En esta escena podrás comprobar el teorema de Pitágoras mediante el procedimiento gráfico de los cuadrados construidos sobre los lados del triángulo.
Actividades y videotutoriales
Autoevaluación sobre triángulos.
Una completa colección de videos sobre triángulos y sus propiedades, con problemas de aplicación.
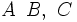 ) y se disponen siguiendo el sentido contrario de las agujas del reloj.
) y se disponen siguiendo el sentido contrario de las agujas del reloj.
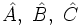
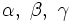 ). También se puede nombrar un ángulo usando tres vértices consecutivos. (Por ejemplo:
). También se puede nombrar un ángulo usando tres vértices consecutivos. (Por ejemplo: 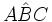
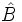
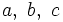 ). También se puede expresar cada lado con dos letras mayúsculas (
). También se puede expresar cada lado con dos letras mayúsculas (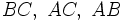 ), las de los vértices contenidos en ese lado.
), las de los vértices contenidos en ese lado.