Plantilla:Area sector circular
De Wikipedia
| Revisión de 11:25 11 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:27 11 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 89: | Línea 89: | ||
| }} | }} | ||
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| - | |titulo1=Ejercicios 1 | + | |titulo1=Ejercicios 2 |
| |duracion=20'42" | |duracion=20'42" | ||
| |sinopsis=2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 2) | |sinopsis=2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 2) | ||
| Línea 95: | Línea 95: | ||
| }} | }} | ||
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| - | |titulo1=Ejercicios 2 | + | |titulo1=Ejercicios 3 |
| |duracion=14'19" | |duracion=14'19" | ||
| |sinopsis=2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 3) | |sinopsis=2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 3) | ||
Revisión de 11:27 11 jun 2017
La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres.
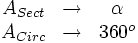
Despejando el área del sector:
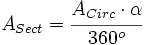
de donde, sustituyendo el área del círculo por su valor, 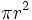 , se obtiene la fórmula.
, se obtiene la fórmula.
Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres.
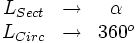
Despejando la longitud del sector:
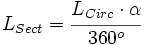
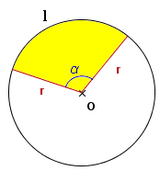
de donde, sustituyendo la longitud de la circunferencia por su valor, 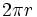 , se obtiene la fórmula.
, se obtiene la fórmula.
En esta escena podrás hallar el área del sector circular y la longitud del arco de circunferencia correspondiente.
Obtención del área de un sector circular. Ejemplo
Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 1)
Fórmula que permite calcular el área de un sector circular a partir del valor del ángulo central. Ejercicios. (Nivel 2)
Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 3)
Fórmula que permite calcular la longitud de un arco de circunferencia a partir del valor del ángulo central. Ejercicios. (Nivel 1)
2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 2)
2 ejercicios que hacen uso de la fórmula de la longitud de un arco de circunferencia. (Nivel 3)
|
Actividad: El sector circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
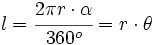
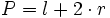
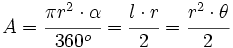
 : radio.
: radio.
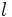 : arco.
: arco.
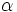 : ángulo (en grados sexagesimales).
: ángulo (en grados sexagesimales).
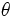 : ángulo
: ángulo  (en radianes).
(en radianes).
 : número Pi = 3,14159...
: número Pi = 3,14159...

