Probabilidad de un suceso (3ºESO)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 07:23 16 jun 2017

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio	Cálculo de probabilidades (SM)		WIRIS Geogebra Calculadora

Ley de los grandes números

Si repetimos un experimento aleatorio bajo las mismas condiciones, llamaremosfrecuencia absoluta de un suceso, al número de veces que ocurre dicho suceso.
Llamaremosfrecuencia relativa de dicho suceso, al cociente entre la frecuencia absoluta y el número total de veces que se realiza el experimento.
La frecuencia relativa es un número comprendido entre 0 y 1.

Frecuencia absoluta y relativa (4'39") Sinopsis:

Frecuencia relativa y frecuencia absoluta. Ejemplo.

Frecuencia absoluta y relativa

Actividad 1 Descripción:

Actividades en las que podrás aprender los conceptos de frecuencia absoluta y relativa.

Actividad 2 Descripción:

Actividades en las que podrás aprender los conceptos de frecuencia absoluta y relativa.

Ley de los grandes números

Un experimento aleatorio se caracteriza porque repetido muchas veces y en idénticas condiciones, su frecuencia relativa tiende a un número fijo, comprendido entre 0 y 1. Esta propiedad es conocida como ley de los grandes números, establecida por Jakob Bernouilli.

Ese número al que tiende la frecuencia es lo que llamaremos probabilidad de un suceso.

Probabilidad de un suceso

Probabilidad de un suceso es el número al que tiende la frecuencia relativa asociada al suceso a medida que aumenta el número de veces que se realiza el experimento.

Probabilidad. Ley de los grandes números Descripción:

Actividades en las que podrás aprender el concepto de probabilidad y la "ley de los grandes números".

Actividad: Probabilidad. Ley de los grandes números Descripción:

En esta escena veremos lo que ocurre cuando tiramos una moneda muchas veces.

Primero tienes que elegir, en la casilla titulada "Múltiplos de", que establece de cuánto en cuánto tiramos las monedas (de 10 en 10, de 100 en 100, etc.).
A continuación, pulsando sobre la flecha azul del control "Tiradas", simularemos el lanzamiento de monedas en la cantidad deseada.
En cada caso obtendremos la frecuencia relativa de cada suceso, y una gráfica con el número de caras.

Prueba con diferentes tiradas y observa el resultado de las frecuencias relativas en cada caso:

Probabilidad. Ley de los grandes números. (13'37") Sinopsis:

La segunda parte de este videotutorial de 33'20" dura 5'38" y trata sobre:

13:35 a 19:19: La probabilidad y la ley de los grandes números. Ejemplos.

Propiedades de la probabilidad

Propiedades

La probabilidad del suceso seguro es 1 y la probabilidad del suceso imposible es 0.
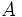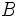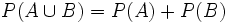Si $A\;$ y $B\;$ son dos sucesos incompatibles, entonces $P(A \cup B)=P(A)+P(B)\;$ .
La suma de las probabilidades de todos los sucesos elementales de un experimento es 1.
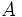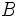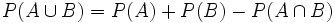Si $A\;$ y $B\;$ son dos sucesos compatibles, entonces $P(A \cup B)=P(A)+P(B)- P(A \cap B)\;$ .
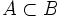Si $A \subset B$ entonces $P(A) < P(B)\;$ .

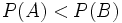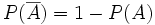$P(\overline{A})=1-P(A)\;$ .
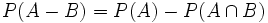$P(A-B)=P(A)-P(A \cap B)\;$ .
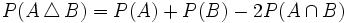$P(A \, \triangle \, B)=P(A)+P(B)-2P(A \cap B)\;$ .
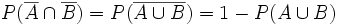$P(\overline{A} \cap \overline{B})=P(\overline{A \cup B})=1-P(A \cup B)\;$ .
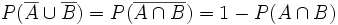$P(\overline{A} \cup \overline{B})=P(\overline{A \cap B})=1-P(A \cap B)\;$ .

Propiedades de la probabilidad

Ejercicio 1 (4'07") Sinopsis:

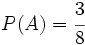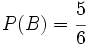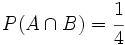Ejercicio 1: Sabiendo que $P(A)=\cfrac{3}{8}\;$ , $P(B)=\cfrac{5}{6}\;$ y $P(A \cap B)=\cfrac{1}{4}\;$ , calcula:

a) 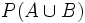$P(A \cup B)\;$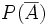

b) $P(\overline{A} )\;$

Ejercicio 2 (4'01") Sinopsis:

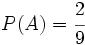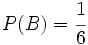Ejercicio 2: Sabiendo que A y B son sucesos incompatibles, y que $P(A)=\cfrac{2}{9}\;$ y $P(B)=\cfrac{1}{6}\;$ , calcula:

a) 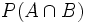$P(A \cap B)\;$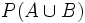

b) $P(A \cup B)\;$

Probabilidad de la diferencia de sucesos (3'25") Sinopsis:

Tutorial sobre la probabilidad de la diferencia de sucesos

Ejercicio 3 (3'00") Sinopsis:

Ejercicio 3: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar sólo el móvil.

Probabilidad de la diferencia simétrica de sucesos (3'02") Sinopsis:

Tutorial sobre la probabilidad de la diferencia simétrica de suscesos.

Ejercicio 4 (3'46") Sinopsis:

Ejercicio 4: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar uno solo de los dos regalos.

Leyes de Morgan (4'03") Sinopsis:

Tutorial sobre las leyes de Morgan.

Ejercicio 5 (3'05") Sinopsis:

Ejercicio 5: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de no ganar ninguno de los dos regalos.

Ejercicio 6 (8'30") Sinopsis:

Ejercicio 6: El 60% de los clientes de una frutería compran naranjas. El 30% no compra ni naranjas ni manzanas. ¿Qué porcentaje de clientes compra manzanas, pero no naranjas?

Ejercicio 7 (5'30") Sinopsis:

Ejercicio 7: En una ciudad, la probabilidad de que llueva un días de junio es del 10%, y de que haga sol un 75%. Si no es posible que en un mismo día de junio llueva y haga sol simultáneamente, ¿cuál es la probabilidad de que en un día de junio no llueva ni haga sol?

Propiedades de la probabilidad Descripción:

Actividades en las que podrás aprender aplicar algunas de las propiedades de la probabilidad.

Obtenido de "http://maralboran.org/wikipedia/index.php/Probabilidad_de_un_suceso_%283%C2%BAESO%29"

Categorías: Matemáticas | Probabilidad

 {{Probabilidad de un suceso}}
 {{p}}
+==Propiedades de la probabilidad==
+{{Propiedades de la probabilidad}}
+{{p}}
 [[Categoría: Matemáticas]][[Categoría: Probabilidad]]

Probabilidad de un suceso (3ºESO)

De Wikipedia

Revisión de 07:23 16 jun 2017

Ley de los grandes números

Probabilidad de un suceso

Propiedades de la probabilidad

Vistas

Herramientas personales

Menú

Buscar

Herramientas