Plantilla:Propiedades de la probabilidad

De Wikipedia

(Diferencia entre revisiones)
Revisión de 07:39 16 jun 2017
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión de 07:39 16 jun 2017
Coordinador (Discusión | contribuciones)

Ir a siguiente diferencia →
Línea 8: Línea 8:
*<math>P(\overline{A})=1-P(A)\;</math>. *<math>P(\overline{A})=1-P(A)\;</math>.
*<math>P(A-B)=P(A)-P(A \cap B)\;</math>. *<math>P(A-B)=P(A)-P(A \cap B)\;</math>.
-*<math>P(A \triangle B)=P(A)+P(B)-2P(A \cap B)\;</math>.+*<math>P(A \, \triangle \, B)=P(A)+P(B)-2P(A \cap B)\;</math>.
}} }}
<center><iframe> <center><iframe>

Revisión de 07:39 16 jun 2017

ejercicio

Propiedades

  • La probabilidad del suceso seguro es 1 y la probabilidad del suceso imposible es 0.
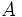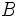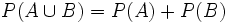  • Si A\; y B\; son dos sucesos incompatibles, entonces P(A \cup B)=P(A)+P(B)\;.
  • La suma de las probabilidades de todos los sucesos elementales de un experimento es 1.
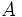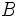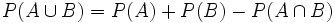  • Si A\; y B\; son dos sucesos compatibles, entonces P(A \cup B)=P(A)+P(B)- P(A \cap B)\;.
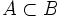  • Si A \subset B entonces P(A) < P(B)\;.
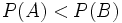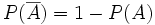  • P(\overline{A})=1-P(A)\;.
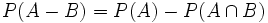  • P(A-B)=P(A)-P(A \cap B)\;.
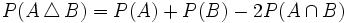  • P(A \, \triangle \, B)=P(A)+P(B)-2P(A \cap B)\;.

video
Propiedades de la probabilidad
Ejercicio 1 (4'07")     Sinopsis:

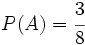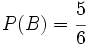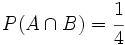Ejercicio 1: Sabiendo que P(A)=\cfrac{3}{8}\; , P(B)=\cfrac{5}{6}\; y P(A \cap B)=\cfrac{1}{4}\;, calcula:

a) 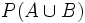P(A \cup B)\;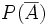

b) P(\overline{A} )\;

Ejercicio 2 (4'01")     Sinopsis:

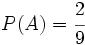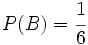Ejercicio 2: Sabiendo que A y B son sucesos incompatibles, y que P(A)=\cfrac{2}{9}\; y P(B)=\cfrac{1}{6}\;, calcula:

a) 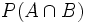P(A \cap B)\;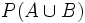

b) P(A \cup B)\;

Probabilidad de la diferencia de sucesos (3'25")     Sinopsis:

Tutorial sobre la probabilidad de la diferencia de sucesos

Problema 1 (3'00")     Sinopsis:

Problema 1: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar sólo el móvil.

Probabilidad de la diferencia simétrica de sucesos (3'02")     Sinopsis:

Tutorial sobre la probabilidad de la diferencia simétrica de suscesos.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Propiedades_de_la_probabilidad"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda