Plantilla:Propiedades de la probabilidad
De Wikipedia
| Revisión de 07:50 16 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:10 16 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 49: | Línea 49: | ||
| }} | }} | ||
| {{Video_enlace_profesor10demates | {{Video_enlace_profesor10demates | ||
| - | |titulo1=Problema 1 | + | |titulo1=Ejercicio 3 |
| |duracion=3'00" | |duracion=3'00" | ||
| - | |sinopsis='''Problema 1:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar sólo el móvil. | + | |sinopsis='''Ejercicio 3:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar sólo el móvil. |
| |url1=https://www.youtube.com/watch?v=CXgeyFV5TMU&index=9&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m31s | |url1=https://www.youtube.com/watch?v=CXgeyFV5TMU&index=9&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m31s | ||
| Línea 64: | Línea 64: | ||
| }} | }} | ||
| {{Video_enlace_profesor10demates | {{Video_enlace_profesor10demates | ||
| - | |titulo1=Problema 2 | + | |titulo1=Ejercicio 4 |
| |duracion=3'46" | |duracion=3'46" | ||
| - | |sinopsis='''Problema 2:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar uno solo de los dos regalos. | + | |sinopsis='''Ejercicio 4:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar uno solo de los dos regalos. |
| |url1=https://www.youtube.com/watch?v=ERU7hIgKgeI&index=11&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m11s | |url1=https://www.youtube.com/watch?v=ERU7hIgKgeI&index=11&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m11s | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Leyes de Morgan | ||
| + | |duracion=4'03" | ||
| + | |sinopsis=Tutorial sobre las leyes de Morgan. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=rt_a9gSL3SQ&index=13&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3t=0m40s | ||
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=3'05" | ||
| + | |sinopsis='''Ejercicio 5:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de no ganar ninguno de los dos regalos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=rt_a9gSL3SQ&index=13&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3t=0m14s | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 08:10 16 jun 2017
Propiedades
- La probabilidad del suceso seguro es 1 y la probabilidad del suceso imposible es 0.
- Si
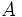 y
y 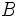 son dos sucesos incompatibles, entonces
son dos sucesos incompatibles, entonces 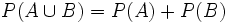 .
.
- La suma de las probabilidades de todos los sucesos elementales de un experimento es 1.
- Si
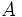 y
y 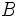 son dos sucesos compatibles, entonces
son dos sucesos compatibles, entonces 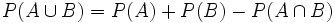 .
.
- Si
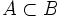 entonces
entonces 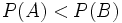 .
.
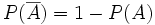 .
.
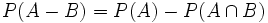 .
.
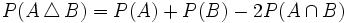 .
.
Ejercicio 1: Sabiendo que 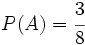 ,
, 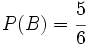 y
y 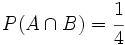 , calcula:
, calcula:
a) 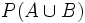
b) 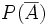
Ejercicio 2: Sabiendo que A y B son sucesos incompatibles, y que 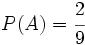 y
y 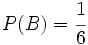 , calcula:
, calcula:
a) 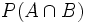
b) 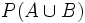
Tutorial sobre la probabilidad de la diferencia de sucesos
Ejercicio 3: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar sólo el móvil.
Tutorial sobre la probabilidad de la diferencia simétrica de suscesos.
Ejercicio 4: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar uno solo de los dos regalos.
Tutorial sobre las leyes de Morgan.
Ejercicio 5: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de no ganar ninguno de los dos regalos.

