Plantilla:Ramas infinitas. Asíntotas (1ºBach)
De Wikipedia
| Revisión de 08:03 19 dic 2016 Coordinador (Discusión | contribuciones) (→Ramas infinitas de las funciones racionales) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas) |
||
| Línea 1: | Línea 1: | ||
| ==Ramas infinitas== | ==Ramas infinitas== | ||
| - | {{Caja_Amarilla|texto=Una función presenta una '''rama infinita''' si presenta una '''asíntota''' o una '''rama parabólica'''.}} | + | {{Ramas infinitas. Asíntotas}} |
| - | {{p}} | + | |
| - | Pasamos a definir asíntota y rama parabólica. | + | |
| - | {{p}} | + | |
| - | ===Asíntota=== | + | |
| - | {{Caja_Amarilla|texto=Una '''asíntota''' es una recta hacia la que se acerca la gráfica de una función, tanto como se quiera, a medida que la variable independiernte se aproxima a un punto, a <math>+ \infty</math> o a <math>-\infty</math>. | + | |
| - | + | ||
| - | Hay tres tipos: | + | |
| - | + | ||
| - | *Asíntota vertical (A.V.) | + | |
| - | *Asíntota horizontal (A.H.) | + | |
| - | *Asíntota oblicua (A.O.) | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | ====Asíntota vertical==== | + | |
| - | {{Tabla75|celda1= | + | |
| - | {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> presenta en <math>x=a\;</math> una '''asíntota vertical''' (A.V.) si ocurre alguna, o ambas, de estas dos cosas: | + | |
| - | + | ||
| - | :<math>\lim_{x \to a^+} f(x)=+ \infty \ \ (\acute{o} \ -\infty)</math> | + | |
| - | + | ||
| - | :<math>\lim_{x \to a^-} f(x)=+ \infty \ \ (\acute{o} \ -\infty)</math> | + | |
| - | ---- | + | |
| - | '''Nota:''' Se pueden dar las dos condiciones o una sola de ellas. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Veamos cómo la función <math>f(x)=\cfrac{x^2}{x-2}</math> presenta una A.V. en <math>x=1\;</math> | + | |
| - | + | ||
| - | En efecto, | + | |
| - | + | ||
| - | :<math>\lim_{x \to 2^-} \cfrac{x^2}{x-2}= -\infty</math> | + | |
| - | :<math>\lim_{x \to 2^+} \cfrac{x^2}{x-2}= +\infty</math> | + | |
| - | ---- | + | |
| - | Haz uso de la siguiente escena de Geogebra para comprobar la solución: | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás representar funciones definidas en hasta 4 trozos. | + | |
| - | |enlace=[https://ggbm.at/JCV99Kf8 Representador de funciones] | + | |
| - | }} | + | |
| - | }} | + | |
| - | |celda2= | + | |
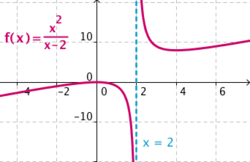
| - | [[Imagen:rama1.png|center|250px]]{{p}}<center>Asíntota vertical: x = 2</center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ====Asíntota horizontal==== | + | |
| - | {{Tabla75|celda1= | + | |
| - | {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> presenta una '''asíntota horizontal''' (A.H.) en <math>y=a\;</math> si: | + | |
| - | + | ||
| - | <center><math>\lim_{x \to +\infty} f(x)= a</math></center> | + | |
| - | + | ||
| - | o bien, | + | |
| - | + | ||
| - | <center><math>\lim_{x \to -\infty} f(x)= a</math></center> | + | |
| - | ---- | + | |
| - | '''Nota:''' Se pueden dar las dos condiciones o una sola de ellas. | + | |
| - | }} | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Veamos cómo la función <math>g(x)=\cfrac{x^2}{x^2+1}</math> presenta una A.H. en <math>y=1\;</math> | + | |
| - | + | ||
| - | En efecto, | + | |
| - | + | ||
| - | :<math>\lim_{x \to +\infty} \cfrac{x^2}{x^2+1}=\lim_{x \to +\infty} \cfrac{x^2}{x^2}= 1</math> | + | |
| - | :<math>\lim_{x \to -\infty} \cfrac{x^2}{x^2+1}=\lim_{x \to -\infty} \cfrac{x^2}{x^2}= 1</math> | + | |
| - | ---- | + | |
| - | Haz uso de la siguiente escena de Geogebra para comprobar la solución: | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás representar funciones definidas en hasta 4 trozos. | + | |
| - | |enlace=[https://ggbm.at/JCV99Kf8 Representador de funciones] | + | |
| - | }} | + | |
| - | }} | + | |
| - | |celda2=[[Imagen:rama3.png|center|250px]]{{p}}<center>Asíntota horizontal: y = 1</center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ====Asíntota oblicua==== | + | |
| - | {{Tabla75|celda1= | + | |
| - | {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> presenta una '''asíntota oblicua''' (A.O.) en <math>y=mx+n\;</math> si: | + | |
| - | + | ||
| - | <center><math>\lim_{x \to +\infty} [f(x)-(mx+n)]= 0</math></center> | + | |
| - | + | ||
| - | o bien, | + | |
| - | + | ||
| - | <center><math>\lim_{x \to -\infty} [f(x)-(mx+n)]= 0</math></center> | + | |
| - | ---- | + | |
| - | '''Nota:''' Se pueden dar las dos condiciones o una sola de ellas. | + | |
| - | ---- | + | |
| - | Para calcular los coeficientes <math>m\;</math> y <math>n\;</math> de la asíntota, se procederá de la siguiente manera: | + | |
| - | + | ||
| - | :<math>m=\lim_{x \to +\infty} \cfrac{f(x)}{x}</math> {{b4}}(o bien, con <math>x \to -\infty</math>) | + | |
| - | + | ||
| - | :<math>n=\lim_{x \to +\infty} [f(x)-mx]</math> {{b4}}(o bien, con <math>x \to -\infty</math>) | + | |
| - | }} | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Veamos cómo la función <math>g(x)=\cfrac{x^2+1}{x-3}</math> presenta una A.O. en <math>y=x+3\;</math> | + | |
| - | + | ||
| - | En efecto, sea <math>y=mx+n\;</math> la A.O., entonces: | + | |
| - | + | ||
| - | :<math>m=\lim_{x \to +\infty} \cfrac{g(x)}{x}=\lim_{x \to +\infty} \cfrac{\cfrac{x^2+1}{x-3}}{x}=\lim_{x \to +\infty} \cfrac{x^2+1}{x(x-3)} =\lim_{x \to +\infty} \cfrac{x^2+1}{x^2-3x}=\lim_{x \to +\infty} \cfrac{x^2}{x^2}=1</math> | + | |
| - | + | ||
| - | :<math>n=\lim_{x \to 1^+} [g(x)-x]= \lim_{x \to +\infty} \left[\cfrac{x^2+1}{x-3}-x \right]= \lim_{x \to +\infty} \cfrac{x^2+1-x^2+3x}{x-3}= \lim_{x \to +\infty} \cfrac{3x+1}{x-3}= \lim_{x \to +\infty} \cfrac{3x}{x}= 3</math> | + | |
| - | + | ||
| - | Para <math>x \to -\infty</math> se obtendrían los mismo valores. | + | |
| - | ---- | + | |
| - | Haz uso de la siguiente escena de Geogebra para comprobar la solución: | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás representar funciones definidas en hasta 4 trozos. | + | |
| - | |enlace=[https://ggbm.at/JCV99Kf8 Representador de funciones] | + | |
| - | }} | + | |
| - | }} | + | |
| - | |celda2= | + | |
| - | [[Imagen:oblicua.png|center|250px]]{{p}}<center>Asíntota oblicua: y = x + 3</center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | ===Rama parabólica=== | + | |
| - | {{Tabla75|celda1= | + | |
| - | {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> presenta una '''rama parabólica''' si no presenta una asíntota oblicua pero cumple que: | + | |
| - | + | ||
| - | <center><math>\lim_{x \to +\infty} f(x)= +\infty \ (\acute{o} -\infty)</math></center> | + | |
| - | + | ||
| - | o bien, | + | |
| - | + | ||
| - | <center><math>\lim_{x \to -\infty} f(x)= +\infty \ (\acute{o} -\infty)</math></center> | + | |
| - | }} | + | |
| - | + | ||
| - | {{p}} | + | |
| - | |celda2= | + | |
| - | [[Imagen:rama2.gif|center|200px]]{{p}}<center>Ramas parabólicas</center> | + | |
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido=Las funciones exponenciales, las polinómicas de grado mayor que 1, las logarítmicas y las irracionales tienen ramas parabólicas. Las dos primeras tienen un crecimiento/decrecimiento más rápido que las dos últimas.}} | + | |
| - | }} | + | |
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
| Línea 150: | Línea 14: | ||
| ==Ramas infinitas de las funciones racionales== | ==Ramas infinitas de las funciones racionales== | ||
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=Consideremos la función racional en la variable x, ya simplificada: | + | {{Ramas infinitas de las funciones racionales}} |
| - | {{p}} | + | |
| - | <center><math>f(x)=\cfrac{P(x)}{Q(x)}=\cfrac{a_nx^n+a_{n-1}x^{n-1}+ \cdots + a_1 x + a_0}{b_m x^m+b_{m-1}x^{m-1}+ \cdots + b_1 x + b_0}\;</math></center> | + | |
| - | {{p}} | + | |
| - | La función <math>f(x)\;</math> tiene las siguientes ramas infinitas: | + | |
| - | *'''ASÍNTOTAS VERTICALES:''' | ||
| - | **Si <math>x=c\;</math> es una raíz de Q(x), entonces la recta <math>x=c\;</math> es una asíntota vertical de <math>f(x)\;</math>. | ||
| - | {{p}} | ||
| - | *'''ASÍNTOTAS HORIZONTALES:''' | ||
| - | **Si <math>n<m\;</math>, entonces la recta <math>y=0\;</math> es una asíntota horizontal de <math>f(x)\;</math>, tanto por <math>+ \infty</math>, como por <math>- \infty</math>. | ||
| - | **Si <math>n=m\;</math>, entonces la recta <math>y=\cfrac{a_n}{b_n}\;</math> es una asíntota horizontal de <math>f(x)\;</math>, tanto por <math>+ \infty</math>, como por <math>- \infty</math>. | ||
| - | {{p}} | ||
| - | *'''ASÍNTOTAS OBLICUAS:''' | ||
| - | **Si <math>n-m=1\;</math>, <math>f(x)\;</math> tienen una asíntota oblicua, tanto por <math>+ \infty</math>, como por <math>- \infty</math>. Dicha asíntota es igual al cociente de la división entre <math>P(x)\;</math> y <math>Q(x)\;</math>. | ||
| - | {{p}} | ||
| - | *'''RAMAS PARABÓLICAS:''' | ||
| - | **Si <math>n-m>1\;</math>, entonces <math>f(x)\;</math> tiene una rama parabólica, tanto por <math>+ \infty</math>, como por <math>- \infty</math>. | ||
| - | }} | ||
| - | {{p}} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
| {{ejercicio | {{ejercicio | ||
| Línea 182: | Línea 28: | ||
| ==Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas== | ==Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas== | ||
| - | ===Funciones trigonométricas=== | + | {{Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas}} |
| - | ===Funciones exponenciales=== | + | |
| - | ===Funciones logartmicas=== | + | |
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
| {{ejercicio | {{ejercicio | ||
Revisión actual
Tabla de contenidos |
Ramas infinitas
Una función presenta una rama infinita si presenta una asíntota o una rama parabólica.
Pasamos a definir asíntota y rama parabólica.
Asíntota
Una asíntota es una recta hacia la que se acerca la gráfica de una función, tanto como se quiera, a medida que la variable independiernte se aproxima a un punto, a  o a
o a  .
.
Hay tres tipos:
- Asíntota vertical (A.V.)
- Asíntota horizontal (A.H.)
- Asíntota oblicua (A.O.)
Nota: La función nunca puede cortar una A.V., pero si puede cortar a una A.H. o a una A.O.
Asíntotas. Tipos.
Asíntota vertical
Una función Nota: Se pueden dar las dos condiciones o una sola de ellas. Veamos cómo la función En efecto, Haz uso de la siguiente escena de Geogebra para comprobar la solución: En esta escena podrás representar funciones definidas en hasta 4 trozos. | Asíntota vertical: x = 2
|
Asíntota horizontal
Una función 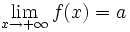 o bien, 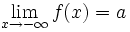 Nota: Se pueden dar las dos condiciones o una sola de ellas. Veamos cómo la función En efecto, Haz uso de la siguiente escena de Geogebra para comprobar la solución: En esta escena podrás representar funciones definidas en hasta 4 trozos. | Asíntota horizontal: y = 1
|
Asíntota oblicua
Una función ![\lim_{x \to +\infty} [f(x)-(mx+n)]= 0](/wikipedia/images/math/b/4/f/b4f57eb5b14023e40e6485b640fd5691.png) o bien, ![\lim_{x \to -\infty} [f(x)-(mx+n)]= 0](/wikipedia/images/math/d/c/1/dc195dc202ab07f6f60038a1570d06b3.png) Nota: Se pueden dar las dos condiciones o una sola de ellas. Para calcular los coeficientes
Veamos cómo la función En efecto, sea Para Haz uso de la siguiente escena de Geogebra para comprobar la solución: En esta escena podrás representar funciones definidas en hasta 4 trozos. | Asíntota oblicua: y = x + 3
|
Rama parabólica
Una función 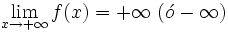 o bien, 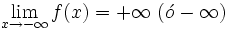 | Ramas parabólicas
|
Las funciones exponenciales, las polinómicas de grado mayor que 1, las logarítmicas y las irracionales tienen ramas parabólicas. Las dos primeras tienen un crecimiento/decrecimiento más rápido que las dos últimas.
Estudio de las asíntotas de una función
Asíntotas. Conceptos básicos. Ejemplos.
Estudio de las asíntotas verticales de una función.
Estudio de las asíntotas horizontales de una función.
Estudio de las asíntotas oblicuas de una función racional (Introducción).
Estudio de las asíntotas oblicuas de una función racional.
Estudio de las asíntotas oblicuas de una función no racional.
Estudia las asíntotas de las siguientes funciones:
|
Actividad: Tendencia de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas |
Ramas infinitas de las funciones racionales
Proposición
Consideremos la función racional en la variable x, ya simplificada (es decir, si el numerador y el denominador tienen factores comunes, cosa que ocurre si se anulan simultáneamente en algún punto, factorizaremos y simplificaremos dichos factores):
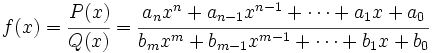
La función  (ya simplificada) tiene las siguientes ramas infinitas, si se da alguno de los siguientes casos:
(ya simplificada) tiene las siguientes ramas infinitas, si se da alguno de los siguientes casos:
- Asíntotas verticales:
- Si
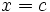 es una raíz de Q(x), entonces la recta
es una raíz de Q(x), entonces la recta 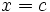 es una asíntota vertical de
es una asíntota vertical de  .
.
- Si
- Asíntotas horizontales:
- Si
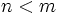 , entonces la recta
, entonces la recta 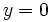 es una asíntota horizontal de
es una asíntota horizontal de  , tanto por
, tanto por  , como por
, como por  .
.
- Si
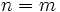 , entonces la recta
, entonces la recta 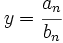 es una asíntota horizontal de
es una asíntota horizontal de  , tanto por
, tanto por  , como por
, como por  .
.
- Si
- Asíntotas oblicuas:
- Si
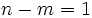 ,
,  tienen una asíntota oblicua, tanto por
tienen una asíntota oblicua, tanto por  , como por
, como por  . Dicha asíntota es igual al cociente de la división entre
. Dicha asíntota es igual al cociente de la división entre  y
y  .
.
- Si
- Ramas parabólicas:
- Si
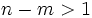 , entonces
, entonces  tiene una rama parabólica, tanto por
tiene una rama parabólica, tanto por  , como por
, como por  .
.
- Si
Obtén las asíntotas de la función 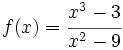
Obtén las asíntotas de la función 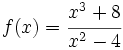
Obtén las asíntotas de las funciones:
Obtén las asíntotas de las funciones:
Estudio de las asíntotas de 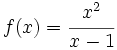 .
Hace un estudio detallado de la posición relativa de la curva respecto de la asíntota oblicua usando el método riguroso de límites.
.
Hace un estudio detallado de la posición relativa de la curva respecto de la asíntota oblicua usando el método riguroso de límites.
Lista de reproducción que consta de 12 vídeos sobre estudio de asíntotas de funciones racionales.
Ejercicios resueltos
Halla todas las ramas infinitas de las siguientes funciones:
- a)
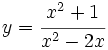 b)
b) 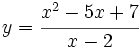 c)
c) 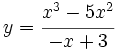
a) A.V.: x=0, x=2; A.H.: y=1
b) A.V.: x=2; A.O.: y=x-3
c) A.V.: x=3; R.I.
Haz uso de la siguiente escena de Geogebra para comprobar las soluciones:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas de las funciones racionales |
Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas
Funciones trigonométricas
Si recordamos las propiedades de las funciones trigonométricas, tenemos:
Propiedades
- Las funciones
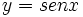 ,
, 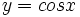 e
e 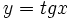 , por ser periódicas, no tienen límite cuando
, por ser periódicas, no tienen límite cuando  ni cuando
ni cuando 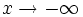 . Por tanto no tienen ramas parabólicas, ni asíntotas horizontales. Las dos primeras tampoco tienen asíntotas verticales por ser su dominio los números reales.
. Por tanto no tienen ramas parabólicas, ni asíntotas horizontales. Las dos primeras tampoco tienen asíntotas verticales por ser su dominio los números reales.
- La función
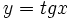 , tiene infinitas asíntotas verticales en los puntos
, tiene infinitas asíntotas verticales en los puntos
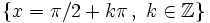
Funciones exponenciales
Si recordamos las propiedades de las funciones exponenciales, tenemos:
Propiedades
La función 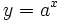 tiene:
tiene:
- Asíntota horizontal:
- En
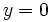 para
para  si
si 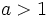
- En
- En
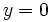 para
para  si
si 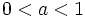
- En
- Rama parabólica:
- Para
 si
si 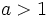
- Para
- Para
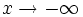 si
si 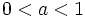
- Para
- Asíntota vertical: No tiene, pués es continua en toda la recta real.
Funciones logartmicas
Si recordamos las propiedades de las funciones logarítmicas, tenemos:
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas |
 una asíntota vertical (A.V.) si ocurre alguna, o ambas, de estas dos cosas:
una asíntota vertical (A.V.) si ocurre alguna, o ambas, de estas dos cosas:
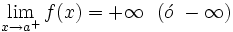
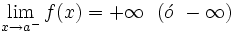
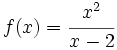 presenta una A.V. en
presenta una A.V. en 
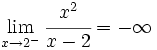
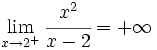
 si:
si:
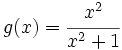 presenta una A.H. en
presenta una A.H. en 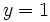
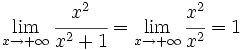
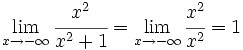

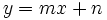 si:
si:
 y
y  de la asíntota, se procederá de la siguiente manera:
de la asíntota, se procederá de la siguiente manera:
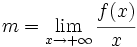 (o bien, con
(o bien, con ![n=\lim_{x \to +\infty} [f(x)-mx]](/wikipedia/images/math/c/d/7/cd758129321f1a26b36d644470fd76f5.png) (o bien, con
(o bien, con 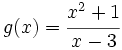 presenta una A.O. en
presenta una A.O. en 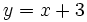
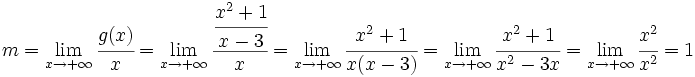
![n=\lim_{x \to 1^+} [g(x)-x]= \lim_{x \to +\infty} \left[\cfrac{x^2+1}{x-3}-x \right]= \lim_{x \to +\infty} \cfrac{x^2+1-x^2+3x}{x-3}= \lim_{x \to +\infty} \cfrac{3x+1}{x-3}= \lim_{x \to +\infty} \cfrac{3x}{x}= 3](/wikipedia/images/math/5/5/e/55e95a0bb6413ed7aa2ce396d251d30d.png)
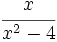
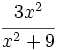
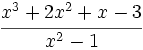
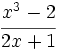
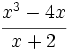
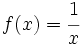 . cuando
. cuando  se hace infinitamente grande.
se hace infinitamente grande.
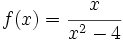
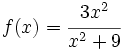
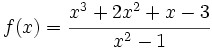
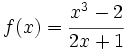
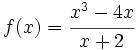
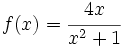
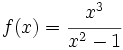
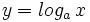 tiene:
tiene:
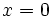 , cuando
, cuando 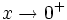 .
.

