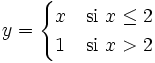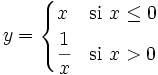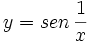Continuidad. Discontinuidades (2ºBach)
De Wikipedia
| Revisión de 10:56 31 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Video_enlace2 | + | {{Menú Matemáticas 2BT |
| - | |titulo1=Continuidad de una función en un punto | + | |ir= |
| - | |duracion=13'37" | + | |ampliar= |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |repasar= |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0302.html | + | |enlaces= |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Discontinuidad evitable | + | |
| - | |duracion=10'09" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0303.html | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{ejemplo2 | + | ==Continuidad de una función en un punto== |
| - | |titulo=Ejemplos: ''Discontinuidad evitable'' | + | {{Continuidad de una función en un punto}} |
| - | |enunciado= | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=1. Ejemplos | + | |
| - | |duracion=6' | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0303_01.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=2. Ejemplos | + | |
| - | |duracion=7'07" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0303_02.html | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Video_enlace2 | + | ==Tipos de discontinuidades== |
| - | |titulo1=Discontinuidad de primera especie | + | {{Tipos de discontinuidades}} |
| - | |duracion=4'57" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0304.html | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{ejemplo2 | + | ==Teorema de Bolzano== |
| - | |titulo=Ejemplos: ''Discontinuidad de primera especie'' | + | {{Video_enlace_fonemato |
| - | |enunciado= | + | |titulo1=Teorema de Bolzano |
| - | {{Video_enlace2 | + | |duracion=4'47" |
| - | |titulo1=1. Ejemplos | + | |sinopsis= |
| - | |duracion=12'05" | + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/03-continuidad-de-funciones-2/09-teorema-de-bolzano-2#.WGOhfEZ9U6c |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0304_01.html | + | |
| }} | }} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_fonemato |
| - | |titulo1=2. Ejemplos | + | |titulo1=La propiedad "D" de Darboux |
| - | |duracion=16'38" | + | |duracion=7'08" |
| |sinopsis=Video tutorial de matematicasbachiller.com | |sinopsis=Video tutorial de matematicasbachiller.com | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0304_02.html | + | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/03-continuidad-de-funciones/10-la-propiedad-bdb-de-darboux#.WGOgyEZ9U6c |
| }} | }} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=3'24" | ||
| + | |sinopsis=¿Se puede afirmar que la función <math>f(x)=x^3-3x^2+5\;</math> toma el valor <math>\sqrt{2}\;</math> en algún punto del intervalo [1,2]? | ||
| + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/05-continuidad-de-funciones/010-ejercicio-4 | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_fonemato |
| - | {{Video_enlace2 | + | |titulo1=Ejercicio 2 |
| - | |titulo1=Discontinuidad de segunda especie | + | |duracion=3'24" |
| - | |duracion=11'06" | + | |sinopsis=Sea la función <math>f(x)=\cfrac{x-1}{x+2}</math>, que cumple que f(-3)=4 y f(-1)=-2, pero cuya gráfica no corta al eje de abscisas en el intervalo [-3,-1]. Razona si esto contradice el teorema de Bolzano. |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/05-continuidad-de-funciones/015-ejercicio-4 |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0305.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Criterios de continuidad | + | |
| - | |duracion=5'01" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0306.html | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{ejemplo2 | + | ==Teorema de Weierstrass== |
| - | |titulo=Ejemplos: ''Criterios de continuidad'' | + | {{Video_enlace_fonemato |
| - | |enunciado= | + | |titulo1=Teorema de Weierstrass |
| - | {{Video_enlace2 | + | |duracion=23'26" |
| - | |titulo1=1. Ejemplos | + | |sinopsis= |
| - | |duracion=13'02" | + | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/03-continuidad-de-funciones/11-teorema-de-weierstrass#.WGOhCUZ9U6c |
| - | |sinopsis=40 ejemplos del estudio de la continuidad de una función. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0306_01.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=2. Ejemplos | + | |
| - | |duracion=13'32" | + | |
| - | |sinopsis=21 ejemplos del estudio de la continuidad de una función. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0306_02.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=3. Ejemplos | + | |
| - | |duracion=10'33" | + | |
| - | |sinopsis=17 ejemplos del estudio de la continuidad de una función. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0306_03.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=4. Ejemplos | + | |
| - | |duracion=8'45" | + | |
| - | |sinopsis=4 ejemplos del estudio de la continuidad de una función. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0306_04.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=5. Ejemplos | + | |
| - | |duracion=15'09" | + | |
| - | |sinopsis=4 ejemplos del estudio de la continuidad de una función. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0306_05.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=5. Ejemplos | + | |
| - | |duracion=9'41" | + | |
| - | |sinopsis=4 ejemplos del estudio de la continuidad de una función. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0306_06.html | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Continuidad en un intervalo | + | |
| - | |duracion=4'19" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0307.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Incremento de una función en un punto | + | |
| - | |duracion=24' | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0312.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=Incremento de una función en un punto y su continuidad en ese punto | + | |
| - | |duracion=6'29" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_03/vdf0313.html | + | |
| }} | }} | ||
| + | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
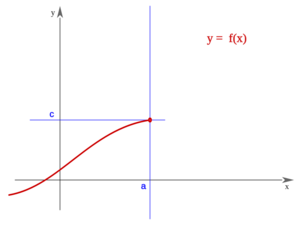
Continuidad de una función en un punto
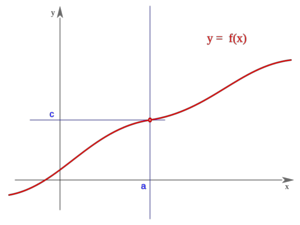
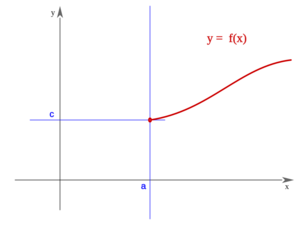
Una función  es continua en un punto
es continua en un punto  , si se cumple que:
, si se cumple que:
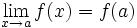
Para que ésto se cumpla deben ocurrir las tres condiciones siguientes:
- La función
 tiene límite en
tiene límite en  : Existe
: Existe 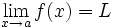
- La función está definida en
 : Existe
: Existe 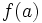
- Los dos valores anteriores coinciden:
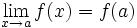
En este vídeo introduciremos el concepto de continuidad de forma gráfica, calculando los límites laterales a partir de la información de la curva.
En este vídeo definiremos cuando una función es continua en un punto usando el concepto de límite y veremos algunos ejemplos en los que usaremos tablas de valores para calcular los límites laterales.
La función "f" se dice continua por la izquierda (derecha) en el punto "a" si el límite de "f" en "a" por la izquierda (derecha) es finito y coincide con f(a). Se dice que "f" es continua en "a" si es continua por la izquierda y por la derecha en "a".
Continuidad de una función. Ejemplos gráficos.
Video tutorial de matematicasbachiller.com
Tipos de discontinuidades
Continuidad de una función en un punto. Tipos de discontinuidades
Ejemplos de los distintos tipos de discontinuidad.
Ejemplos gráficos de los distintos tipos de discontinuidad.
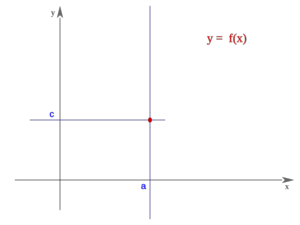
Una función  tiene una discontinuidad evitable en un punto
tiene una discontinuidad evitable en un punto  si existe
si existe 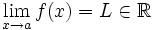 pero éste no coincide con
pero éste no coincide con 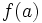 , bien porque
, bien porque  no esté definida en
no esté definida en  o bien porque simplemente sean distintos.
o bien porque simplemente sean distintos.
Discontinuidad evitable
Evitable (no definida en un punto, tiene un hueco)
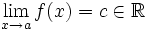 , pero , pero 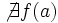 | Evitable (punto desplazado que deja un hueco)
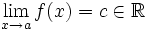 , pero , pero 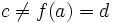 |
Ejemplo: Discontinuidad evitable
Comprueba en qué puntos presentan las siguientes funciones una discontinuidad evitable:
- a)
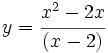 b)
b) 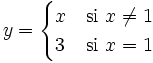
a) En x=2 tiene una discontinuidad evitable.
b) En x=2 tiene una discontinuidad evitable.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar las soluciones:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
La función "f" presenta "discontinuidad evitable" en el punto "a" si tiene límite finito en "a" pero no coincide con f(a). El términos geométricos significa que la gráfica de "f" tiene un "agujerito" en "a". Se "evita" la discontinuidad "rellenando" el agujerito; y para ello basta redefinir "f" de modo que f(a) coincida con el límite de "f" en "a".
Ejemplos
Ejercicio de examen para Ministro
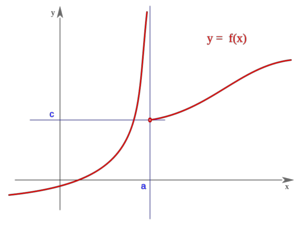
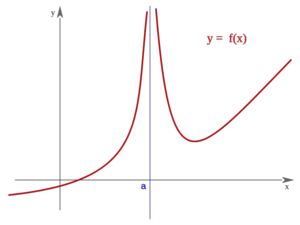
Discontinuidad esencial de primera especie
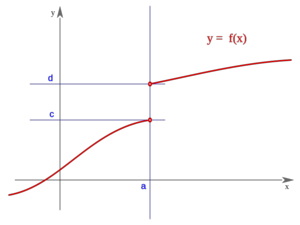
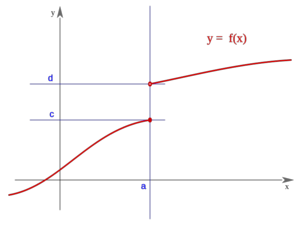
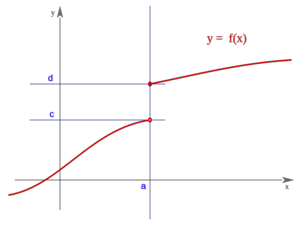
Una función  tiene una discontinuidad esencial de primera especie de salto finito en un punto
tiene una discontinuidad esencial de primera especie de salto finito en un punto  si existen los límites laterales en dicho punto y son finitos, pero estos no coinciden:
si existen los límites laterales en dicho punto y son finitos, pero estos no coinciden:
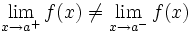
Se llama salto al valor absoluto de la diferencia enter ambos límites:
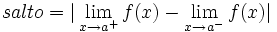
Nota: 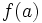 puede estar definida o no, y puede coincidir o no con uno de los dos límites laterales.
puede estar definida o no, y puede coincidir o no con uno de los dos límites laterales.
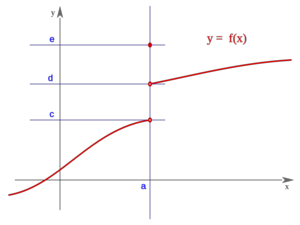
Salto finito (Salto=d-c)
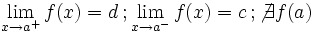 | Salto finito (Salto=d-c)
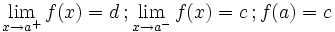 |
Salto finito (Salto=d-c)
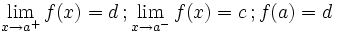 | Salto finito (Salto=d-c)
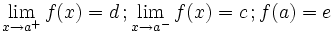 |
Ejemplo: Discontinuidad de salto finito
Comprueba en qué punto presenta la siguiente función una discontinuidad de salto finito y averigua el valor del salto:
En x=2 tiene una discontinuidad de salto finito. El salto es igual a | 2 − 1 | = 1.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
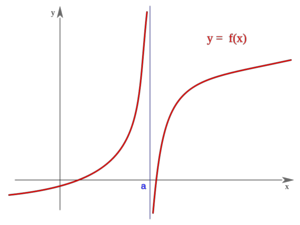
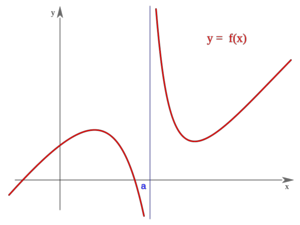
Una función  tiene una discontinuidad esencial de primera especie de salto infinito si existen los límites laterales, siendo uno finito y otro infinito.
tiene una discontinuidad esencial de primera especie de salto infinito si existen los límites laterales, siendo uno finito y otro infinito.
Nota: 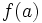 puede estar definida o no, y puede coincidir o no con el límite lateral finito.
puede estar definida o no, y puede coincidir o no con el límite lateral finito.
Salto infinito
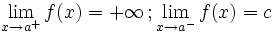 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" | Salto infinito
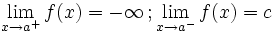 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" |
Salto infinito
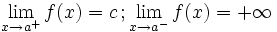 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" | Salto infinito
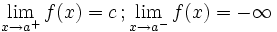 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" |
Ejemplo: Discontinuidad de salto infinito
Comprueba en qué punto presenta la siguiente función una discontinuidad de salto ifinito:
En x=0 tiene una discontinuidad de salto infinito.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
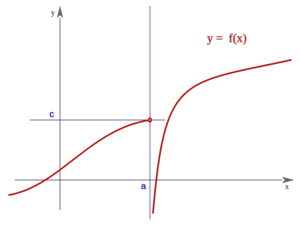
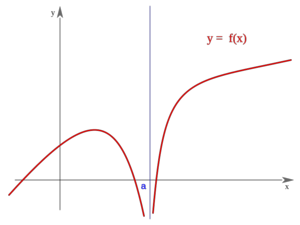
Una función  tiene una discontinuidad esencial de primera especie asintótica si si existen los límites laterales, siendo ambos + o - infinito, pero no necesariamente iguales.
tiene una discontinuidad esencial de primera especie asintótica si si existen los límites laterales, siendo ambos + o - infinito, pero no necesariamente iguales.
Nota: 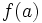 puede estar definida o no.
puede estar definida o no.
Asintótica
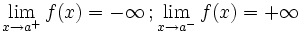 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo | Asintótica
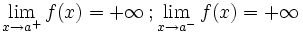 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo |
Asintótica
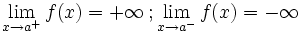 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo | Asintótica
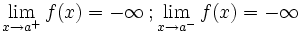 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo |
Ejemplo: Discontinuidad asintótica
Comprueba en qué puntos presentan las siguientes funciones una discontinuidad asintótica:
- a)
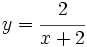 b)
b) 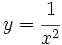
a) En x=-2 tiene una discontinuidad asintótica.
b) En x=0 tiene una discontinuidad asintótica.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
La función "f" presenta "discontinuidad de primera especie" en el punto "a" si los límites laterales de "f" en "a" son distintos. El términos geométricos significa que la gráfica de "f" da un "salto" en "a".
3 ejercicios sobre discontinuidades de primera especie
3 ejercicios sobre discontinuidades de primera especie
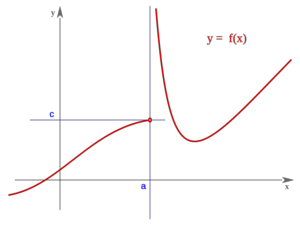
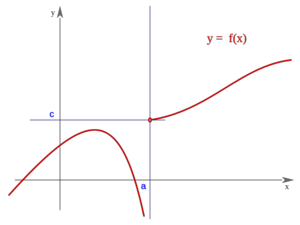
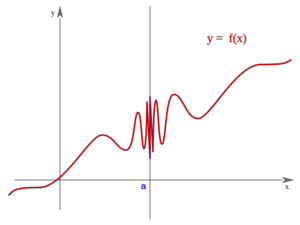
Discontinuidad esencial de segunda especie
Una función  tiene una discontinuidad de segunda especie si no existe alguno de los límites laterales.
tiene una discontinuidad de segunda especie si no existe alguno de los límites laterales.
Nota: 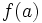 puede estar definida o no.
puede estar definida o no.
Segunda especie
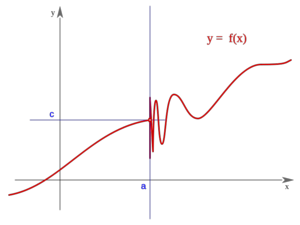
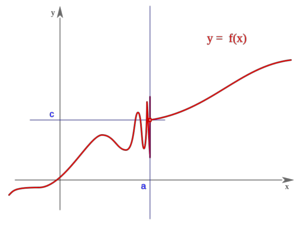
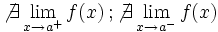 Es oscilante por ambos lados"f(a)" puede estar definida o no Es oscilante por ambos lados"f(a)" puede estar definida o no | Segunda especie
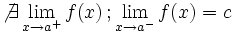 Es oscilante por la derecha"f(a)" puede estar definida o no Es oscilante por la derecha"f(a)" puede estar definida o no | Segunda especie
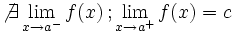 Es oscilante por la izquierda"f(a)" puede estar definida o no Es oscilante por la izquierda"f(a)" puede estar definida o no |
Ejemplo: Discontinuidad de segunda especie
Comprueba en qué punto presenta la siguiente función una discontinuidad de segunda especie:
En x=0 tiene una discontinuidad de segunda especie.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Algunos autores incluyen dentro de las discontinuidades de segunda especie los siguientes casos:
No hay función a la derecha de a
| No hay función a la izquierda de a
| No hay función ni a la derecha ni a la izquierda de a
|
No obstante, en estos casos, nosotros no diremos que la función sea discontinua en "a". Para explicar esto con rigor es necesario recurrir a la definición formal de continuidad que se verá en cursos posteriores.
Como ejemplo de esto que estamos diciendo tienes el siguiente video:
La función "f" presenta "discontinuidad de segunda especie" en el punto "c" si no existe alguno de los límites laterales de "f" en "c".
Teorema de Bolzano
Video tutorial de matematicasbachiller.com
¿Se puede afirmar que la función 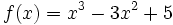 toma el valor
toma el valor 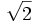 en algún punto del intervalo [1,2]?
en algún punto del intervalo [1,2]?
Sea la función 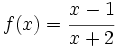 , que cumple que f(-3)=4 y f(-1)=-2, pero cuya gráfica no corta al eje de abscisas en el intervalo [-3,-1]. Razona si esto contradice el teorema de Bolzano.
, que cumple que f(-3)=4 y f(-1)=-2, pero cuya gráfica no corta al eje de abscisas en el intervalo [-3,-1]. Razona si esto contradice el teorema de Bolzano.