Bisectriz de un ángulo (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:04 4 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:06 4 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | ==Bisectriz de un ángulo== | ||
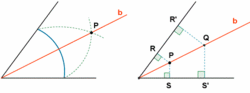
| + | {{Tabla50|celda2=[[Imagen:bisectriz.gif|thumb|250px|La recta "b" es la bisectriz del ángulo. Cualquier punto (P o Q) de ella, equidista de los lados del ángulo (PR = PS, QR'=QS').]] | ||
| + | |celda1= | ||
| + | {{Caja_Amarilla|texto=Se llama '''bisectriz''' de un ángulo a la semirrecta que, partiendo del vértice, lo divide en dos ángulos iguales.}} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Propiedad|enunciado=Los puntos de la bisectriz de un ángulo equidistan de los lados del mismo.}} | ||
| + | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Bisectriz de un ángulo|descripcion=Actividad en la que podrás ver la bisectriz de un ángulo y la propiedad de que sus puntos equidistan de los lados del ángulo. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_4a.htm | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Construcción de la mediatriz== | ||
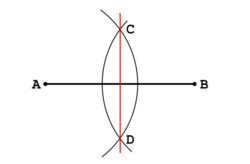
| + | {{Tabla75|celda2=[[Imagen:mediatriz.png|thumb|250px|Construcción de la mediatriz de un segmento con regla y compás.]] | ||
| + | |celda1= | ||
| + | Vamos a construir la mediatriz de un segmento utilizando regla y compás: | ||
| + | |||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | ||
| + | #Representa dos puntos y traza el segmento que los une utilizando la regla. | ||
| + | #Coloca el compás sobre uno de los extremos del segmento y ábrelo para que coincida con el otro extremo. Traza así una circunferencia. Haz la misma operación apoyando el compás sobre el otro extremo y sin variar su abertura. | ||
| + | #Une ahora los puntos donde se cortan las dos circunferencias que acabas de trazar. El nuevo segmento es perpendicular al inicial y si lo prolongas obtendrás la recta mediatriz que buscabas. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_pdd|titulo1=Mediatriz de un segmento | ||
| + | |duracion=2'09" | ||
| + | |url1=https://www.youtube.com/watch?v=1SKQFJDOi_Y | ||
| + | |sinopsis=En este vídeo trazamos la mediatriz de un segmento. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Construcción de la mediatriz|descripcion=Actividad en la que podrás ver un video de cómo se construye la mediatriz de un segmento, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_2b.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver cómo se construye la mediatriz de un segmento, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan. | ||
| + | |enlace=[https://ggbm.at/NQS44af3 Construcción de la mediatriz] | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 18:06 4 jul 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Bisectriz de un ángulo
Se llama bisectriz de un ángulo a la semirrecta que, partiendo del vértice, lo divide en dos ángulos iguales.  Propiedad Los puntos de la bisectriz de un ángulo equidistan de los lados del mismo.  Bisectriz de un ángulo Descripción: Actividad en la que podrás ver la bisectriz de un ángulo y la propiedad de que sus puntos equidistan de los lados del ángulo. |  |
Construcción de la mediatriz
| Vamos a construir la mediatriz de un segmento utilizando regla y compás:
Procedimiento
 Mediatriz de un segmento (2'09") Sinopsis: En este vídeo trazamos la mediatriz de un segmento. Construcción de la mediatriz Descripción: Actividad en la que podrás ver un video de cómo se construye la mediatriz de un segmento, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan.  Construcción de la mediatriz Descripción: En esta escena podrás ver cómo se construye la mediatriz de un segmento, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan. |  |
