Simetrías (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:51 17 jul 2017 Coordinador (Discusión | contribuciones) (→Simetría axial) ← Ir a diferencia anterior |
Revisión de 16:51 17 jul 2017 Coordinador (Discusión | contribuciones) (→Simetría axial) Ir a siguiente diferencia → |
||
| Línea 39: | Línea 39: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Figura simétrica respecto de un eje== | ||
| {{Caja_Amarilla|texto=Una figura plana diremos que es '''simétrica respecto de un eje''', si cualquier punto de la figura tiene su simétrico respecto de dicho eje en la propia figura. Esto significa, que si doblásemos la figura por el eje de simetría, las dos mitades coincidirían.}} | {{Caja_Amarilla|texto=Una figura plana diremos que es '''simétrica respecto de un eje''', si cualquier punto de la figura tiene su simétrico respecto de dicho eje en la propia figura. Esto significa, que si doblásemos la figura por el eje de simetría, las dos mitades coincidirían.}} | ||
| {{p}} | {{p}} | ||
Revisión de 16:51 17 jul 2017
Simetría axial
 Procedimiento Dado un punto A, para obtener su simétrico, A', respecto de una recta "e", se siguen los siguientes pasos:
|  |
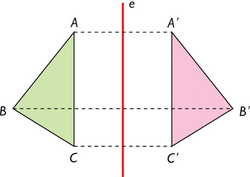
Figura simétrica respecto de un eje
Una figura plana diremos que es simétrica respecto de un eje, si cualquier punto de la figura tiene su simétrico respecto de dicho eje en la propia figura. Esto significa, que si doblásemos la figura por el eje de simetría, las dos mitades coincidirían.
Proposición
Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes contiguos forman un ángulo de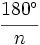 
.
