Plantilla:Propiedades de la probabilidad
De Wikipedia
| Revisión de 10:22 15 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Teorema_sin_demo|titulo=Propiedades|enunciado= | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| - | *La suma de las probabilidades de todos los sucesos elementales de un experimento es 1. | ||
| *La probabilidad del '''suceso seguro''' es 1 y la probabilidad del '''suceso imposible''' es 0. | *La probabilidad del '''suceso seguro''' es 1 y la probabilidad del '''suceso imposible''' es 0. | ||
| *Si <math>A\;</math> y <math>B\;</math> son dos sucesos '''incompatibles''', entonces <math>P(A \cup B)=P(A)+P(B)\;</math>. | *Si <math>A\;</math> y <math>B\;</math> son dos sucesos '''incompatibles''', entonces <math>P(A \cup B)=P(A)+P(B)\;</math>. | ||
| + | *La suma de las probabilidades de todos los sucesos elementales de un experimento es 1. | ||
| *Si <math>A\;</math> y <math>B\;</math> son dos sucesos '''compatibles''', entonces <math>P(A \cup B)=P(A)+P(B)- P(A \cap B)\;</math>. | *Si <math>A\;</math> y <math>B\;</math> son dos sucesos '''compatibles''', entonces <math>P(A \cup B)=P(A)+P(B)- P(A \cap B)\;</math>. | ||
| + | *Si <math>A \subset B</math> entonces <math>P(A) < P(B)\;</math>. | ||
| + | |||
| *<math>P(\overline{A})=1-P(A)\;</math>. | *<math>P(\overline{A})=1-P(A)\;</math>. | ||
| + | *<math>P(A-B)=P(A)-P(A \cap B)\;</math>. | ||
| + | *<math>P(A \, \triangle \, B)=P(A)+P(B)-2P(A \cap B)\;</math>. | ||
| + | *<math>P(\overline{A} \cap \overline{B})=P(\overline{A \cup B})=1-P(A \cup B)\;</math>. | ||
| + | *<math>P(\overline{A} \cup \overline{B})=P(\overline{A \cap B})=1-P(A \cap B)\;</math>. | ||
| }} | }} | ||
| - | <center><iframe> | + | {{animación probabilidad}} |
| - | url=http://maralboran.org/web_ma/wiki_Estadistica/Azar_y_Probabilidad/probable.html | + | |
| - | width=100% | + | |
| - | height=100 | + | |
| - | name=myf50me | + | |
| - | </iframe></center> | + | |
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Propiedades de la probabilidad|enunciado= | ||
| {{Video_enlace_profesor10demates | {{Video_enlace_profesor10demates | ||
| - | |titulo1=Ejercicio | + | |titulo1=Ejercicio 1 |
| |duracion=4'07" | |duracion=4'07" | ||
| - | |sinopsis=Sabiendo que <math>P(A)=\cfrac{3}{8}\;</math>, <math>P(B)=\cfrac{5}{6}\;</math> y <math>P(A \cap B)=\cfrac{1}{4})\;</math>, calcula: | + | |sinopsis='''Ejercicio 1:''' Sabiendo que <math>P(A)=\cfrac{3}{8}\;</math> , <math>P(B)=\cfrac{5}{6}\;</math> y <math>P(A \cap B)=\cfrac{1}{4}\;</math>, calcula: |
| a) <math>P(A \cup B)\;</math> | a) <math>P(A \cup B)\;</math> | ||
| Línea 22: | Línea 24: | ||
| b) <math>P(\overline{A} )\;</math> | b) <math>P(\overline{A} )\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=HMFrC-8Hlw4&index=6&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3 | + | |url1=https://www.youtube.com/watch?v=HMFrC-8Hlw4&index=6&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m50s |
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=4'01" | ||
| + | |sinopsis='''Ejercicio 2:''' Sabiendo que A y B son sucesos incompatibles, y que <math>P(A)=\cfrac{2}{9}\;</math> y <math>P(B)=\cfrac{1}{6}\;</math>, calcula: | ||
| + | |||
| + | a) <math>P(A \cap B)\;</math> | ||
| + | |||
| + | b) <math>P(A \cup B)\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=vHNEY7R8ntg&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3&index=7#t=0m30s | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Probabilidad de la diferencia de sucesos | ||
| + | |duracion=3'25" | ||
| + | |sinopsis=Tutorial sobre la probabilidad de la diferencia de sucesos | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=yLO6xpI00oc&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3&index=8#t=0m13s | ||
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=3'00" | ||
| + | |sinopsis='''Ejercicio 3:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar sólo el móvil. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=CXgeyFV5TMU&index=9&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m31s | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Probabilidad de la diferencia simétrica de sucesos | ||
| + | |duracion=3'02" | ||
| + | |sinopsis=Tutorial sobre la probabilidad de la diferencia simétrica de suscesos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=TpHnAwNsXEQ&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3&index=10#t=0m8s | ||
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=3'46" | ||
| + | |sinopsis='''Ejercicio 4:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar uno solo de los dos regalos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=ERU7hIgKgeI&index=11&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3#t=0m11s | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Leyes de Morgan | ||
| + | |duracion=4'03" | ||
| + | |sinopsis=Tutorial sobre las leyes de Morgan. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=rt_a9gSL3SQ&index=13&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3t=0m40s | ||
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=3'05" | ||
| + | |sinopsis='''Ejercicio 5:''' En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de no ganar ninguno de los dos regalos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=rt_a9gSL3SQ&index=13&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3t=0m14s | ||
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=8'30" | ||
| + | |sinopsis='''Ejercicio 6:''' El 60% de los clientes de una frutería compran naranjas. El 30% no compra ni naranjas ni manzanas. ¿Qué porcentaje de clientes compra manzanas, pero no naranjas? | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=ioK9_zH7_Kg&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3&index=30 | ||
| + | }} | ||
| + | {{Video_enlace_profesor10demates | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=5'30" | ||
| + | |sinopsis='''Ejercicio 7:''' En una ciudad, la probabilidad de que llueva un días de junio es del 10%, y de que haga sol un 75%. Si no es posible que en un mismo día de junio llueva y haga sol simultáneamente, ¿cuál es la probabilidad de que en un día de junio no llueva ni haga sol? | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=S-wNelGaJxE&index=31&list=PLunRFUHsCA1zpwjJvZOapw78qPj3WOWt3 | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Propiedades de la probabilidad | ||
| + | |descripcion=Actividades en las que podrás aprender aplicar algunas de las propiedades de la probabilidad. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena12/3quincena12_contenidos_2c.htm | ||
| }} | }} | ||
Revisión actual
Propiedades
- La probabilidad del suceso seguro es 1 y la probabilidad del suceso imposible es 0.
- Si
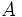 y
y 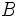 son dos sucesos incompatibles, entonces
son dos sucesos incompatibles, entonces 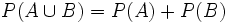 .
.
- La suma de las probabilidades de todos los sucesos elementales de un experimento es 1.
- Si
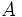 y
y 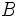 son dos sucesos compatibles, entonces
son dos sucesos compatibles, entonces 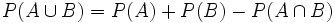 .
.
- Si
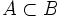 entonces
entonces 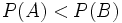 .
.
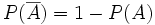 .
.
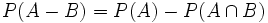 .
.
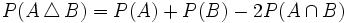 .
.
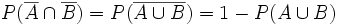 .
.
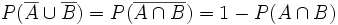 .
.
Ejercicio 1: Sabiendo que 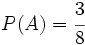 ,
, 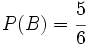 y
y 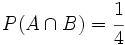 , calcula:
, calcula:
a) 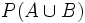
b) 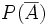
Ejercicio 2: Sabiendo que A y B son sucesos incompatibles, y que 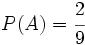 y
y 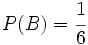 , calcula:
, calcula:
a) 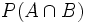
b) 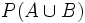
Tutorial sobre la probabilidad de la diferencia de sucesos
Ejercicio 3: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar sólo el móvil.
Tutorial sobre la probabilidad de la diferencia simétrica de suscesos.
Ejercicio 4: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de ganar uno solo de los dos regalos.
Tutorial sobre las leyes de Morgan.
Ejercicio 5: En un concurso se puede ganar un reloj, un móvil o ambos regalos a la vez. Si la probabilidad de ganar un reloj es 0.4, la de ganar un móvil 0.2 y la de ganar los dos regalos es 0.05, calcula la probabilidad de no ganar ninguno de los dos regalos.
Ejercicio 6: El 60% de los clientes de una frutería compran naranjas. El 30% no compra ni naranjas ni manzanas. ¿Qué porcentaje de clientes compra manzanas, pero no naranjas?
Ejercicio 7: En una ciudad, la probabilidad de que llueva un días de junio es del 10%, y de que haga sol un 75%. Si no es posible que en un mismo día de junio llueva y haga sol simultáneamente, ¿cuál es la probabilidad de que en un día de junio no llueva ni haga sol?
Actividades en las que podrás aprender aplicar algunas de las propiedades de la probabilidad.

