Problemas de proporcionalidad inversa (1º ESO)
De Wikipedia
| Revisión de 16:16 6 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 7: | Línea 7: | ||
| __TOC__ | __TOC__ | ||
| {{p}} | {{p}} | ||
| - | ==Problemas de proporcionalidad inversa== | ||
| - | {{Video_enlace_clasematicas | ||
| - | |titulo1=Relaciones de proporcinalidad inversa | ||
| - | |duracion=15'51" | ||
| - | |sinopsis=Tutorial que explica los problemas de proporcionalidad inversa, viendo los métodos de igualdad de productos, método general, reducción a la unidad y regla de tres inversa. | ||
| - | |url1=https://www.youtube.com/watch?v=MtC5DVMFkL4&list=PLZNmE9BEzVIkOdmbGm3jJH7F7sf1hpvYa&index=3 | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| (Pág. 156) | (Pág. 156) | ||
| ==Método de reducción a la unidad== | ==Método de reducción a la unidad== | ||
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=El '''método de reducción a la unidad''' consiste en averiguar el valor la segunda magnitud si la primera vale 1 (la unidad). A partir de esa información, es fácil sacar los demás valores de la segunda magnitud a partir de los de la primera, ya que sólo tendremos que dividir la primera magnitud por dicho valor.}} | + | {{Método de reducción a la unidad (inversa) 1ºESO}} |
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | + | |
| - | Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos? | + | |
| - | ---- | + | |
| - | '''Solución:''' | + | |
| - | + | ||
| - | Primero averiguamos lo que tarda 1 grifo (la unidad): | + | |
| - | + | ||
| - | Nº grifos Tiempo (h) | + | |
| - | ---------- ---------- | + | |
| - | 2 --------> 6 | + | |
| - | 1 --------> x | + | |
| - | + | ||
| - | :<math>x=6 \cdot 2 = 12</math> h | + | |
| - | + | ||
| - | {{b4}} | + | |
| - | + | ||
| - | A partir del tiempo que tarda 1 grifo es fácil sacar el que tardan 3 grifos: | + | |
| - | + | ||
| - | Nº grifos Tiempo (h) | + | |
| - | --------- ---------- | + | |
| - | 1 --------> 12 | + | |
| - | 3 --------> x | + | |
| - | + | ||
| - | :<math>x = \cfrac {12}{3} = 4 </math> h | + | |
| - | }} | + | |
| - | {{p}} | + | |
| ==Regla de tres inversa== | ==Regla de tres inversa== | ||
| - | {{p}}{{Teorema_sin_demo|titulo=Procedimiento|enunciado=La '''regla de tres inversa''' es un método que se apoya en el hecho de que al multiplicar dos magnitudes directamente proporcionales el producto no varía. Esto permite establecer una ecuación de la cual se obtiene el valor desconocido.}} | + | {{Regla de tres inversa}} |
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| - | Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos? | ||
| - | ---- | ||
| - | '''Solución:''' | ||
| - | Nº grifos Tiempo (h) | + | ==Actividades y videotutoriales== |
| - | --------- ---------- | + | {{Actividades y videotutoriales: Regla de tres inversa}} |
| - | 2 --------> 6 | + | |
| - | 3 --------> x | + | |
| - | + | ||
| - | :<math> 2 \cdot 6 = 3 \cdot x \ \rightarrow \ x = \cfrac{2 \cdot 6}{3} = 4</math> h | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ==Actividades== | + | |
| - | {{ejemplos de regla de tres simple inversa}} | + | |
| - | {{p}} | + | |
| - | {{AI_enlace|titulo1=Actividades: ''Problemas de proporcionalidad inversa'' | + | |
| - | |descripcion= | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/09/04.htm | + | |
| - | width=800 | + | |
| - | height=650 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/09/04.htm | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=Resuelve problemas de regla de tres simple. Tendrás que averiguar si son directas o inversas. | + | |
| - | |enlace=[https://ggbm.at/Y5KRHjKt Problemas: Regla de tres simple directa e inversa] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Línea 99: | Línea 31: | ||
| }} | }} | ||
| - | [[Categoría: Ejercicios de Matemáticas|Números]] | + | [[Categoría: Matemáticas]][[Categoría: Aritmética]] |
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 156)
Método de reducción a la unidad
Procedimiento
Dadas dos magnitudes inversamente proporcionales, el método de reducción a la unidad consiste en averiguar el valor la segunda magnitud si la primera vale 1 (la unidad). Ese valor obtenido es la constante de proporcionalidad inversa. A partir de esa información, es fácil sacar los demás valores de la segunda magnitud a partir de los de la primera, ya que sólo tendremos que dividir dicho valor por la primera magnitud.
Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos?
Solución:
Primero averiguamos lo que tarda 1 grifo (la unidad):
Nº grifos Tiempo (h)
---------- ----------
2 --------> 6
1 --------> x
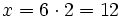 h
h
A partir del tiempo que tarda 1 grifo es fácil sacar el que tardan 3 grifos:
Nº grifos Tiempo (h)
--------- ----------
1 --------> 12
3 --------> x
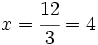 h
h
Actividades para que aprendas y practiques el método de reducción a la unidad con relaciones de proporcionalidad inversas.
Regla de tres inversa
Procedimiento
La regla de tres inversa es un método que se apoya en el hecho de que al multiplicar dos magnitudes directamente proporcionales el producto no varía. Esto permite establecer una ecuación de la cual se obtiene el valor desconocido.
Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos?
Solución:
Nº grifos Tiempo (h)
--------- ----------
2 --------> 6
3 --------> x
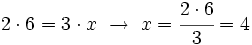 h
h
Actividades para que aprendas y practiques la regla de tres inversa.
Actividades y videotutoriales
Tutorial que explica los problemas de proporcionalidad inversa, viendo los métodos de igualdad de productos, método general, reducción a la unidad y regla de tres inversa.
Problemas de proporcionalidad inversa:
- Manuel ha hecho la mudanza de su casa en 6 viajes, utilizando para ello su coche, en el que caben 300 kg. ¿Cuántos viajes haría si hubiese alquilado una furgoneta con capacidad para 360 kg?
- Un ciclista que viaja a 22 km/h tarda 45 min en cubrir la contrareloj del día. ¿Cuánto tardaría si fuera a 33 km/h?
- Necesitamos 15 obreros para levantar un muro en 1 hora. ¿Cuántos obreros se necesitan para levantarlo en tres cuartos de hora?. ¿Y para levantarlo en 20 min?
Tutorial que explica los problemas de proporcionalidad inversa.
Tutorial que explica los problemas de proporcionalidad inversa.
Si 25 jardineros tardan 12 días en podar los árboles de un parque, ¿cuántos jardineros harán falta para realizar el mismo trabajo en 10 días?
Toma 20 min en llenar un tanque con un grifo que tiene un caudal de 20 litros/seg. Si se utiliza un grifo que arroja 9 litros/seg más que el anterior, ¿en cuánto tiempo se llenará el tanque?
Practica distintos problemas de proporcionalidad inversa.
Resuelve problemas de regla de tres simple inversa.
Problemas de autoevaluación sobre la regla de tres simple inversa.
Ejercicios y problemas de autoevaluación sobre proporcionalidad inversa.
Resuelve problemas de regla de tres simple. Tendrás que averiguar si son directas o inversas.
Ejercicios propuestos
|
Ejercicios propuestos: Problemas de proporcionalidad inversa |

