Plantilla:Triángulos semejantes
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:58 24 abr 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | Se dice que dos figuras geométricas, y en particular dos [[triángulos]], son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes. | + | Se dice que dos figuras geométricas, y en particular dos [[triángulos]], son [[Figuras semejantes (2º ESO)|semejantes]] si tienen la misma forma aunque sus tamaños u orientación sean diferentes. |
| {{p}} | {{p}} | ||
| - | |||
| Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera: | Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera: | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| - | {{Tabla50 | + | {{Tabla75 |
| |celda1={{p}} | |celda1={{p}} | ||
| - | *Dos [[triángulos]] son '''semejantes''' si cumplen que: | + | *Dos [[triángulos]], {{sube|porcentaje=20%|contenido=<math>ABC\;</math>}} y {{sube|porcentaje=20%|contenido=<math>A'B'C'\;</math>}}, son '''semejantes''', y lo notaremos {{sube|porcentaje=20%|contenido=<math>ABC \sim A'B'C'\;</math>}}, si cumplen las dos condiciones siguientes: |
| {{p}} | {{p}} | ||
| :1. Los '''ángulos''' correspondientes u homólogos* son iguales: | :1. Los '''ángulos''' correspondientes u homólogos* son iguales: | ||
| Línea 23: | Línea 22: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | '''Nota:''' Cuando veamos los criterios de semejanza de triángulos, veremos que para que dos triángulos sean semejantes bastará con que se cumpla una de las dos condiciones: que los lados homólogos sean proporcionales o que los ángulos homólogos sean iguales. En tal caso, la otra condición se cumplirá automáticamente. | ||
| + | |||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Triángulos semejantes|enunciado= | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Tutorial | ||
| + | |duracion=2'13" | ||
| + | |sinopsis=Definición de triángulos semejantes. | ||
| + | |url1=https://www.youtube.com/watch?v=0Z3Ke00MDkU | ||
| + | }} | ||
| + | ---- | ||
| {{Video_enlace_unicoos | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejemplo: Triángulos semejantes | + | |titulo1=Ejemplo |
| |duracion=5'09" | |duracion=5'09" | ||
| - | |sinopsis=Resolución de problemas mediante sistemas de ecuaciones lineales | + | |sinopsis=Ejemplo de semejanza de triángulos. |
| |url1=http://www.unicoos.com/clase/matematicas/2-eso/semejanza-y-teorema-de-thales/semejanza/semejanza-de-triangulos-01 | |url1=http://www.unicoos.com/clase/matematicas/2-eso/semejanza-y-teorema-de-thales/semejanza/semejanza-de-triangulos-01 | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
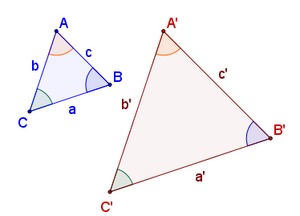
Se dice que dos figuras geométricas, y en particular dos triángulos, son semejantes si tienen la misma forma aunque sus tamaños u orientación sean diferentes.
Matemáticamente, la semejanza de triángulos la podemos expresar de la siguiente manera:
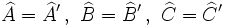
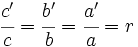
|
(*) Dos elementos de dos figuras son homólogos si ocupan el mismo lugar en ambas figuras.
Nota: Cuando veamos los criterios de semejanza de triángulos, veremos que para que dos triángulos sean semejantes bastará con que se cumpla una de las dos condiciones: que los lados homólogos sean proporcionales o que los ángulos homólogos sean iguales. En tal caso, la otra condición se cumplirá automáticamente.
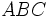
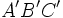
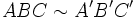
 se le llama razón de semejanza.
se le llama razón de semejanza.